运筹说 第103期 | 非线性规划经典例题讲解

发布时间：2024年01月16日

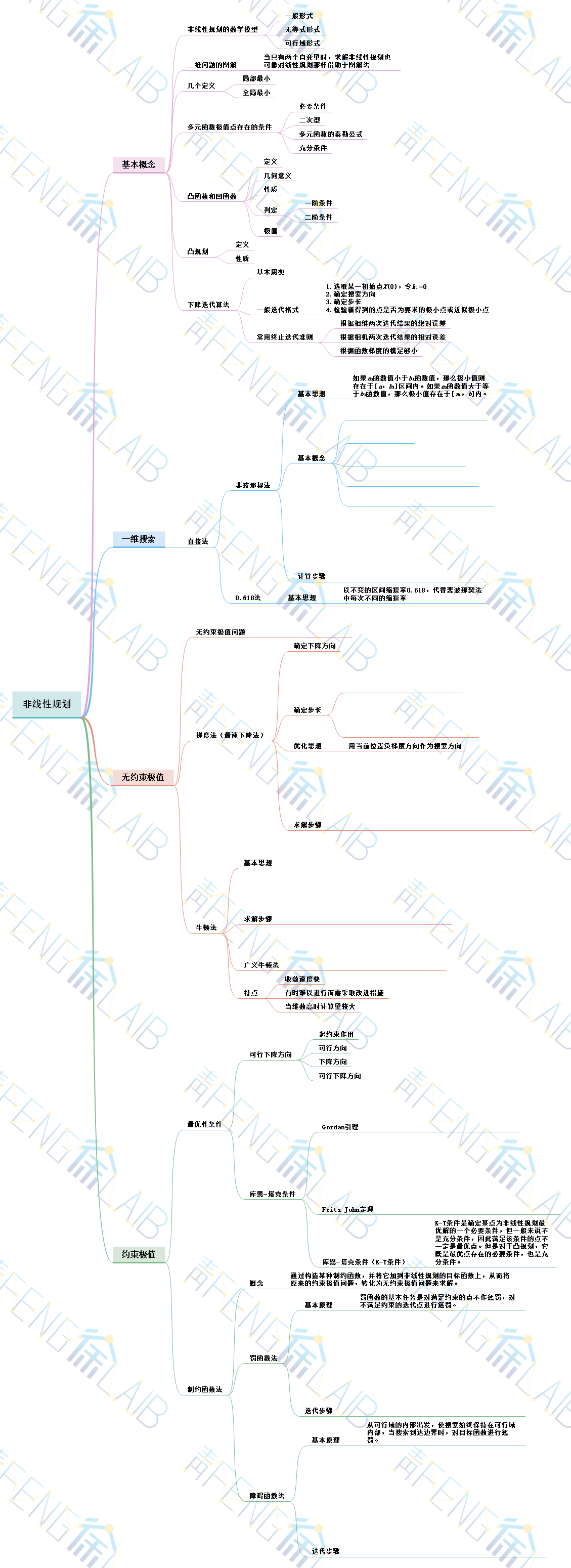
通过前几期的学习，我们已经学会了非线性规划的基本概念、一维搜索的计算方法，其中掌握了斐波那契法、0.618法（黄金分割法）、库恩塔克条件以及无约束极值问题的定义与相关求解方法，本期小编带大家学习非线性规划在经济管理中的应用。

在实际工作中，我们能发现非线性规划在经济管理中有着许多应用，本期小编选择了其中一些典型例子，包括一维搜索的两种求解方法、梯度下降法以及库恩塔克条件，进行详细讲解。

一、一维搜索求解

问题描述：

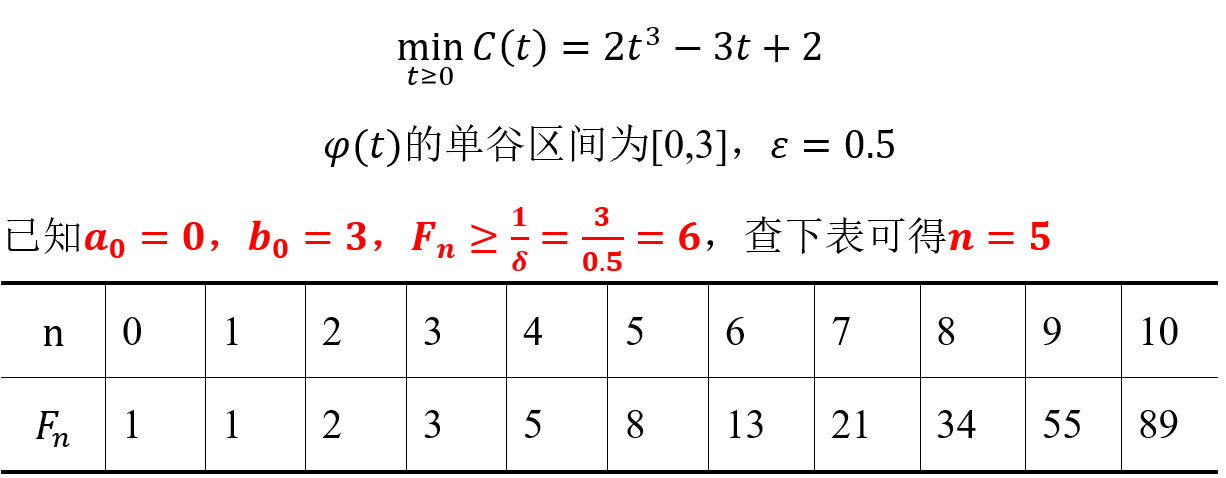
现有一家制造企业，生产某种产品所需的能源消耗与生产速度相关，其目的是希望通过优化生产速度来最小化能源消耗，并在给定的时间范围内完成生产任务。现已知能源消耗与生产速度之间的关系由函数\varphi \left ( t \right )=t^{3}-2t+1决定，其中t表示生产速度(t≥0)，起始时间和结束时间对应的生产速度为0和3，要求区间精度为\varepsilon =0.5。

问题分析：

该问题的目标是在给定的时间范围内生产产品，并在满足速度取值范围和区间精度的条件下最小化能源消耗，寻找一个最佳的生产速度t，故可以将问题转换成一维搜索方法进行求解。根据以上描述可以得出初始的单谷区间，并根据要求确定最后区间的精度，根据斐波那契法或者0.618法（黄金分割法）进行迭代，得到最佳的生产速度。

问题求解：

斐波那契法求解：

根据上述描述可得出：

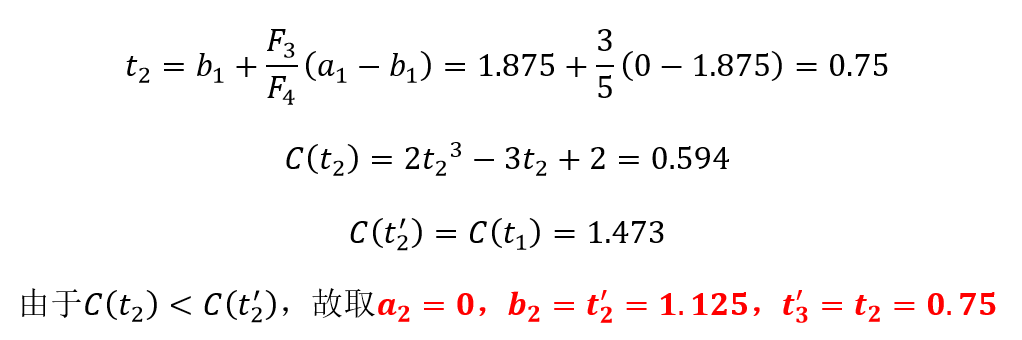
0.618法（黄金分割法）求解：

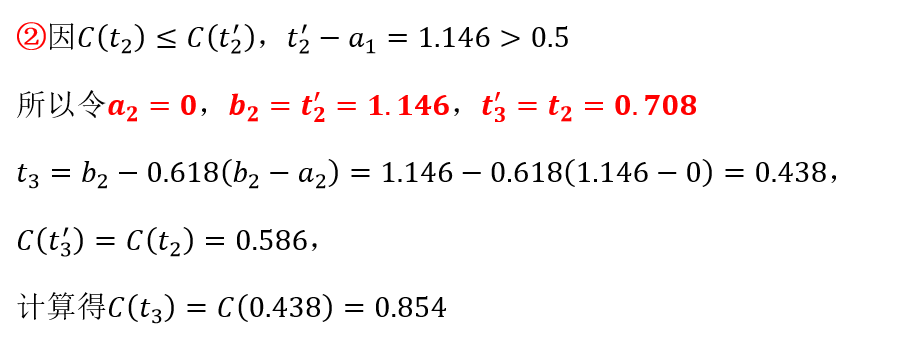
方法总结

黄金分割法和斐波那契法都是用于求解一维搜索问题的优化算法，特别在非线性规划中有广泛的应用。它们的目标是在一个给定的区间内找到一个局部最优解，即使函数是非线性的。下面是它们的相同点以及不同点的总结。

相同点

①一维搜索： 黄金分割法和斐波那契法都是一维搜索方法，适用于只有一个变量的优化问题。

②基于区间缩减： 两种方法都利用不断缩小搜索区间的策略，从而逐步逼近最优解。

③无需梯度信息： 这两种方法不需要函数的梯度信息，因此适用于无法轻易获得导数信息的问题。

不同点

搜索点选取方式：

①黄金分割法： 黄金分割法使用恒定的比例因子将当前搜索区间分成两个部分，选择一个新的搜索点进行迭代。

②斐波那契法： 斐波那契法根据斐波那契数列的特性来决定搜索点的位置，通过适当的调整搜索区间来达到收敛。

二、梯度下降法求解

问题描述：

假设你是一家公司的销售经理，负责优化某个产品的销售策略。根据历史数据和市场分析，你确定了一个销售指标公式 f\left ( x\right )=-x_{1_{}}-x_{2_{}}+2x_{1}^{2}+2x_1 x_2+x_2^2?来评估不同的销售策略，其中，销售策略的参数由x_{1} 和 x_{2}描述，表示采用不同的促销手段和定价策略，为了确保销售策略的可行性，促销手段和定价策略均不能为负值。根据给定的指标公式，你应该如何确定最佳的销售策略参数，以使得该指标最小？(终止误差\varepsilon=0.3 )

问题解析：

三、库恩塔克条件

问题描述：

某一施工单位希望设计一座跨越一条河流的桥梁，为了提高桥梁的性能，需要使得函数f\left ( X\right )=2x_{1}^{2}+2x_1 x_2+x_2^2-10x_{1}-10x_{2} 最小，希望桥梁在材料使用和结构设计上能够达到最佳的效果，以提高桥梁的承重能力、稳定性和耐久性。其中，变量x_{1}?和x_{2}?分别代表桥梁的设计参数。为了避免过分复杂的结构和不切实际的设计，桥梁的设计参数的取值必须满足x_{1}^{2}+x_{2}^{2}\leqslant 5 。另外，桥梁的设计参数x_{1}?和x_{2}?的线性组合必须满足3x_{1}+x_{2}\leqslant 6 。

问题分析：

根据上述对问题的描述，可以明确的看出该优化问题是在有约束条件下求取最小值，我们可以使用库恩-塔克条件来解决。通过对约束条件引入广义拉格朗日乘子，分情况对引入的约束条件进行讨论，如果可以找到一组满足库恩-塔克条件的可行点和广义拉格朗日乘子，就能够找到该问题的最优点。

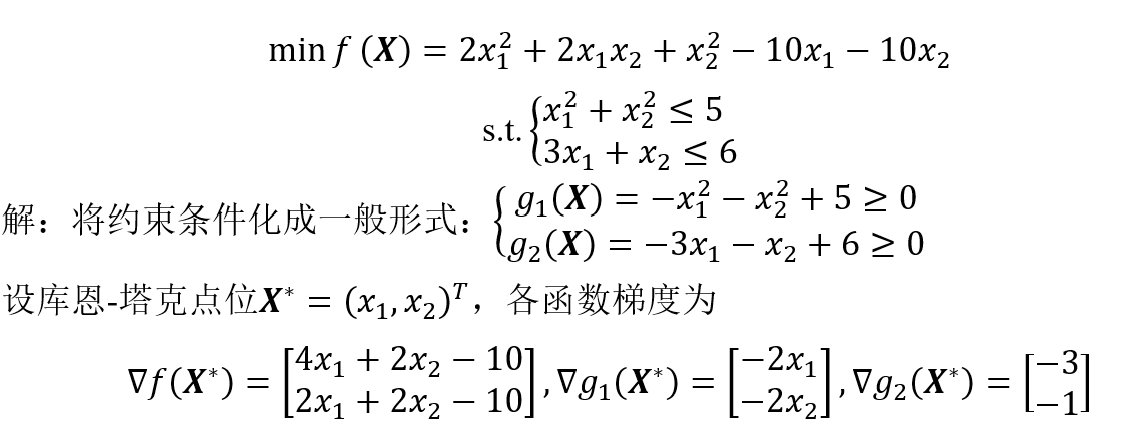
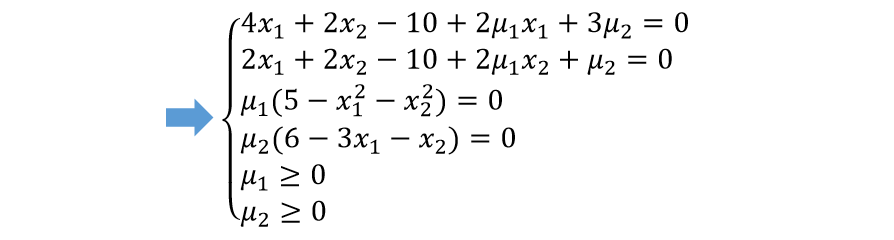
以上就是本期非线性规划例题讲解的全部内容啦，通过对这一期的学习，相信大家一定能够加深对非线性规划的理解，进而在生活实践中学会应用！

作者 | 林鑫 马书良

责编 | 陈梦

审核 | 徐小峰

?·YUNCHOUSHUO·?

·知乎｜运筹说·

·B站｜运筹说·

·CSDN｜运筹说·

文章来源:https://blog.csdn.net/YUNCHOUSHUO/article/details/135621235
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章