强化学习(三)有限马尔可夫决策过程
1、智能体与环境
马尔科夫决策过程是通过与环境互动进行学习的直接框架,决策者称为智能体,智能体之外的一切称为环境,它们不断交互,智能体选择动作,环境反馈给智能体新的状态和奖励。
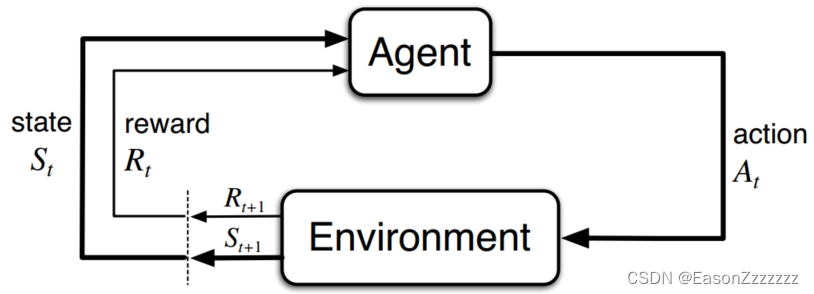
具体地说,智能体与环境交互时,随着时间步的推移,产生形以下的序列:
S
0
,
A
0
,
R
1
,
S
1
,
A
1
,
R
2
,
S
2
,
A
2
,
R
3
,
?
S_0,A_0,R_1,S_1,A_1,R_2,S_2,A_2,R_3,\cdots
S0?,A0?,R1?,S1?,A1?,R2?,S2?,A2?,R3?,?
其中, S , A S,A S,A 和 R R R 分别对应状态、动作和奖励。
在有限马尔可夫决策过程中,
S
,
A
S,A
S,A 和
R
R
R 的集合都具有有限数量的元素,在这种情况下,随机变量
R
t
R_t
Rt? 和
S
t
S_t
St? 可以被定义为离散概率分布,且仅依赖前一状态和动作,即
p
(
s
′
,
r
∣
s
,
a
)
?
P
r
{
S
t
=
s
′
,
R
t
=
r
∣
S
t
?
1
=
s
,
A
t
?
1
=
a
}
s
′
,
s
∈
S
,
r
∈
R
,
a
∈
A
(
s
)
p(s^\prime,r|s,a)\doteq Pr\{S_t=s^\prime,R_t=r |S_{t-1}=s,A_{t-1}=a\}\quad\quad\quad s^\prime,s\in\cal{S},r\in\cal{R},a\in\cal{A}(s)
p(s′,r∣s,a)?Pr{St?=s′,Rt?=r∣St?1?=s,At?1?=a}s′,s∈S,r∈R,a∈A(s)
p
p
p 的概率完全表征了系统的动态过程,
S
t
S_t
St? 和
R
t
R_t
Rt? 的每个可能值的概率只取决于之前的状态
S
t
?
1
S_{t-1}
St?1?和动作
A
t
?
1
A_{t-1}
At?1? 而与更早的状态和动作无关。它是一个具有四个参数的确定性函数,满足
∑
s
′
∈
S
∑
r
∈
R
p
(
(
s
′
,
r
∣
s
,
a
)
=
1
\sum_{s^\prime\in\cal{S}}\sum_{r\in\cal{R}}p((s^\prime,r|s,a)=1
s′∈S∑?r∈R∑?p((s′,r∣s,a)=1
由四参数动态函数
p
p
p 可以计算出任何关于环境的信息,例如状态转移概率
p
(
s
′
∣
s
,
a
)
?
P
r
{
S
t
=
s
′
∣
S
t
?
1
=
s
,
A
t
?
1
=
a
}
=
∑
r
∈
R
p
(
s
′
,
r
∣
s
,
a
)
p(s^\prime|s,a)\doteq Pr\{S_t=s^\prime|S_{t-1}=s,A_{t-1}=a\}=\sum_{r\in\cal{R}}p(s^\prime,r|s,a)
p(s′∣s,a)?Pr{St?=s′∣St?1?=s,At?1?=a}=r∈R∑?p(s′,r∣s,a)
2、目标和奖励
在强化学习中,智能体的目的或目标被抽象成一个特殊的信号,称为奖励。智能体的目标是最大化其获得的奖励总量,使用奖励信号来形式化目标是强化学习最显著的特征之一。
乍一看通过奖励信号来实现目标好像不太合理,但是实践过程中它很灵活。例如,为了让机器人学会走路,可以在每个时间步设置与机器人向前运动成正比的奖励;让机器人学会如何逃离迷宫,可以设置每经过一个时间步给 -1 的奖励。从这些例子中可以看出,智能体总是最大化它的奖励总量,因此我们设置的奖励必须真正表明我们希望完成的任务。
3、收益和回合
到目前为止,我们知道,智能体的目标是最大化其累计获得的奖励,如果在时间步长
t
t
t 之后获得的奖励序列为
R
t
+
1
,
R
t
+
2
,
R
t
+
3
,
?
R_{t+1},R_{t+2},R_{t+3},\cdots
Rt+1?,Rt+2?,Rt+3?,?,我们希望最大化的是收益,记作
G
t
G_t
Gt?,收益即是奖励的总和:
G
t
?
R
t
+
1
+
R
t
+
2
+
R
t
+
3
+
?
+
R
T
G_t\doteq R_{t+1}+R_{t+2}+R_{t+3}+\cdots+R_{T}
Gt??Rt+1?+Rt+2?+Rt+3?+?+RT?
其中 T T T 是最终时间步。当智能体-环境的交互可以分解为子序列时,称之为回合。例如玩游戏,走出迷宫,每一个回合都以终端状态结束,然后重置到起始状态,我们称之为回合任务。
但在很多时候,智能体和环境的交互不能自然地分解为回合,而是无限制地持续进行,我们称之为持续任务,那么收益就不能以上述公式计算了,因为
T
=
∞
T=\infty
T=∞,收益本身就很容易是无穷大的。我们需要另外一个概念:折扣,即
G
t
?
R
t
+
1
+
γ
R
t
+
2
+
γ
2
R
t
+
3
+
?
=
∑
k
=
0
∞
γ
k
R
t
+
k
+
1
G_t\doteq R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}+\cdots=\sum_{k=0}^\infty\gamma^kR_{t+k+1}
Gt??Rt+1?+γRt+2?+γ2Rt+3?+?=k=0∑∞?γkRt+k+1?
其中 γ \gamma γ 是一个参数, 0 ≤ γ ≤ 1 0\leq\gamma\leq1 0≤γ≤1,称之为折扣率。
当
γ
=
0
\gamma = 0
γ=0 时,可以认为智能体是“短视”的,因为它只关心最大化眼前的奖励。而当
γ
→
1
\gamma\rightarrow1
γ→1 时,可以认为智能体是“远见”的,因为智能体更强烈地考虑未来的奖励。
G
t
?
R
t
+
1
+
γ
R
t
+
2
+
γ
2
R
t
+
3
+
γ
3
R
t
+
4
+
?
=
R
t
+
1
+
γ
(
R
t
+
2
+
γ
R
t
+
3
+
γ
2
R
t
+
4
+
?
?
)
=
R
t
+
1
+
γ
G
t
+
1
\begin{aligned} G_t&\doteq R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}+\gamma^3R_{t+4}+\cdots\\ &=R_{t+1}+\gamma( R_{t+2}+\gamma R_{t+3}+\gamma^2 R_{t+4}+\cdots)\\ &=R_{t+1}+\gamma G_{t+1} \end{aligned}
Gt???Rt+1?+γRt+2?+γ2Rt+3?+γ3Rt+4?+?=Rt+1?+γ(Rt+2?+γRt+3?+γ2Rt+4?+?)=Rt+1?+γGt+1??
这种方法可以使得计算收益变得容易。虽然收益是无穷级数,但当 γ < 0 \gamma<0 γ<0,它是收敛的。
4、回合任务和持续任务的统一符号
前一节中,我们介绍了两种强化学习任务:回合任务和持续任务。为了进行统一,有必要建立一种可以同时讨论这两种任务的符号。
在回合任务中,我们考虑的不是一个长时间步骤序列,而是一系列的回合,每个回合都由有限个时间步骤序列组成,因此在编号时不仅要考虑时间步 t t t,还要考虑回合数 i i i。但是,当我们考虑回合任务时,我们没必要区分不同的回合,也就是放弃对回合进行编号。回合任务中,收益为有限个数之和,在持续任务中,收益为无限个数之和,这两者可以通过将回合终止视为一种特殊状态统一起来,这种状态只会向自身过渡,并且只产生零奖励。
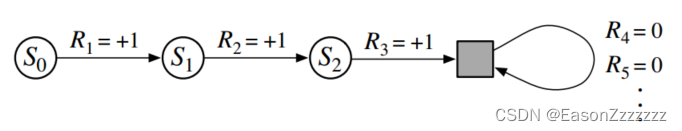
5、策略和价值函数
几乎所有的强化学习算法都涉及估计价值函数—状态价值函数(或状态-动作价值函数),用于评价智能体在给定状态下的表现(或在给定状态下执行给定动作的表现)的好坏,这里“好坏”是根据预期的未来收益来定义的。当然,智能体在未来获得的收益的期望取决于它将采取什么动作,因此价值函数是根据特定的动作方式(策略)来定义的。
策略是从状态到可能动作的概率的映射,如果智能体在时间步 t t t 遵循策略 π \pi π,则 π ( a ∣ s ) \pi(a|s) π(a∣s) 是 S t = s S_t=s St?=s 时 A t = a A_t=a At?=a 的概率。
策略
π
\pi
π 下状态
s
s
s 的价值函数是从状态
s
s
s 开始之后的期望收益,记为
v
π
(
s
)
v_\pi(s)
vπ?(s),有
v
π
(
s
)
?
E
[
G
t
∣
S
t
=
s
]
=
E
[
∑
k
=
0
∞
γ
k
R
t
+
k
+
1
∣
S
t
=
s
]
v_\pi(s)\doteq \Bbb{E}[G_t|S_t=s]=\Bbb{E}\Big[\sum_{k=0}^\infty\gamma^kR_{t+k+1}\Big| S_t=s\Big]
vπ?(s)?E[Gt?∣St?=s]=E[k=0∑∞?γkRt+k+1?
?St?=s]
其中, E [ ? ] \Bbb{E}[\cdot] E[?] 表示智能体在遵循策略 π \pi π 的情况下随机变量的期望值,我们称 v π v_\pi vπ? 为策略 π \pi π 的状态价值函数。
同样,策略
π
\pi
π 下,在状态
s
s
s 下采取动作
a
a
a 的价值函数是从状态
s
s
s、动作
a
a
a 开始之后的期望收益,记为
q
π
(
s
,
a
)
q_\pi(s,a)
qπ?(s,a),有
q
π
(
s
,
a
)
?
E
[
G
t
∣
S
t
=
s
,
A
t
=
a
]
=
E
[
∑
k
=
1
∞
γ
k
R
t
+
k
+
1
∣
S
t
=
s
,
A
t
=
a
]
q_\pi(s,a)\doteq \Bbb{E}[Gt|S_t=s,A_t=a]=\Bbb{E}\Big[\sum_{k=1}^\infty\gamma^kR_{t+k+1}\Big| S_t=s,A_t=a\Big]
qπ?(s,a)?E[Gt∣St?=s,At?=a]=E[k=1∑∞?γkRt+k+1?
?St?=s,At?=a]
我们称 q π q_\pi qπ? 为策略 π \pi π 的动作价值函数。
价值函数 v π v_\pi vπ? 和 q π q_\pi qπ? 可以根据过去的经验估计,例如,智能体遵循策略 π \pi π,那么当遇到某状态的次数趋于无穷时,那么该状态收益的平均值将收敛于该状态的价值 v π ( s ) v_\pi(s) vπ?(s),状态-动作的价值 q π ( s ) q_\pi(s) qπ?(s) 也是如此,我们称这种估计方法为蒙特卡罗方法,因为它们是对大量随机样本的实际收益进行平均。当然,如果有很多的状态,那么这种方法可能不太实际(需要单独保存每个状态的收益平均值)。
在强化学习和动态规划中价值函数的一个基本属性是它们满足递归关系,
v
π
(
s
)
?
E
π
[
G
t
∣
S
t
=
s
]
=
E
π
[
R
t
+
1
+
γ
G
t
+
1
∣
S
t
=
s
]
=
∑
a
π
(
a
∣
s
)
∑
s
′
∑
r
p
(
s
′
,
r
∣
s
,
a
)
[
r
+
γ
E
[
G
t
+
1
∣
S
t
+
1
=
s
′
]
]
=
∑
a
π
(
a
∣
s
)
∑
s
′
,
r
p
(
s
′
,
r
∣
s
,
a
)
[
r
+
γ
v
π
(
s
′
)
]
\begin{aligned} v_\pi(s)&\doteq \Bbb{E}_\pi[G_t|S_t=s]\\ &=\Bbb{E}_\pi[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ &=\sum_a\pi(a|s)\sum_{s^\prime}\sum_r p(s^\prime,r|s,a)\Big[r+\gamma\Bbb{E}[G_{t+1}|S_{t+1}=s^\prime]\Big]\\ &=\sum_a\pi(a|s)\sum_{s^\prime,r}p(s^\prime,r|s,a)\Big[r+\gamma v_\pi(s^\prime)\Big] \end{aligned}
vπ?(s)??Eπ?[Gt?∣St?=s]=Eπ?[Rt+1?+γGt+1?∣St?=s]=a∑?π(a∣s)s′∑?r∑?p(s′,r∣s,a)[r+γE[Gt+1?∣St+1?=s′]]=a∑?π(a∣s)s′,r∑?p(s′,r∣s,a)[r+γvπ?(s′)]?
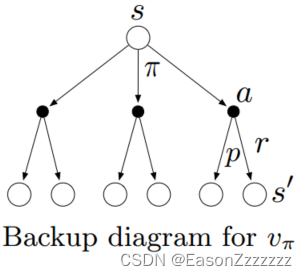
上式为
v
π
v_\pi
vπ? 的贝尔曼方程,它表达了一个状态的价值函数与其下一个状态的价值函数之间的关系,如下图所示,从顶部的状态
s
s
s 开始,智能体可以采取三种动作的任意一个,环境反馈下一状态
s
′
s^\prime
s′(图中有两种状态,环境反馈其中一种)以及奖励
r
r
r,需要注意的是
s
′
s^\prime
s′ 和
r
r
r 取决于状态转移概率
p
p
p。贝尔曼方程根据概率对每种可能进行加权,它指出初始状态的价值必须等于预期的下一状态的(折扣)价值加上沿途预期的奖励。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!