[LeetCode Hot100热题 ] 详解LC 105 从前序和中序遍历序列构造二叉树

目录

题干

先序遍历和中序遍历的简要介绍

思路

完整代码

---

题干

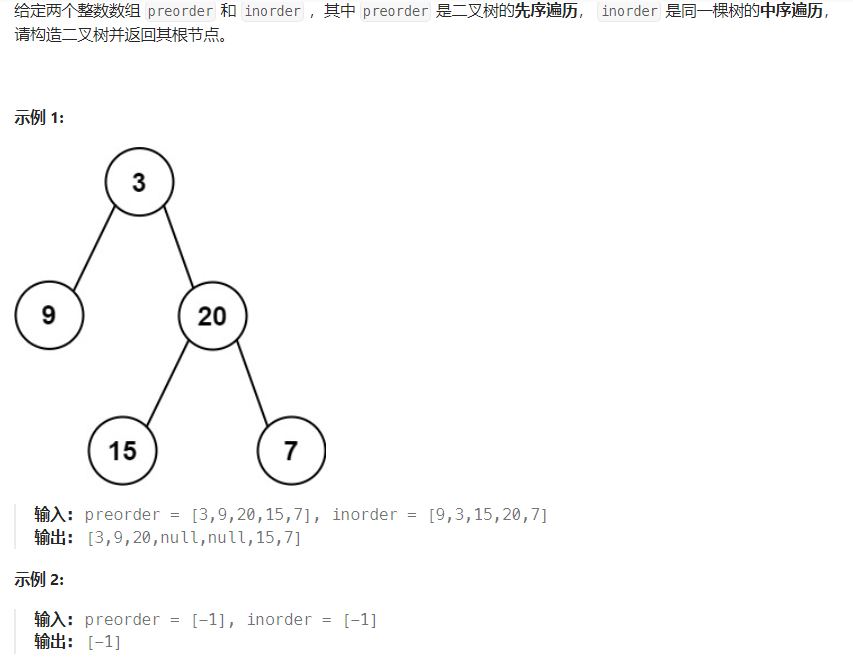
提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

先序遍历和中序遍历的简要介绍

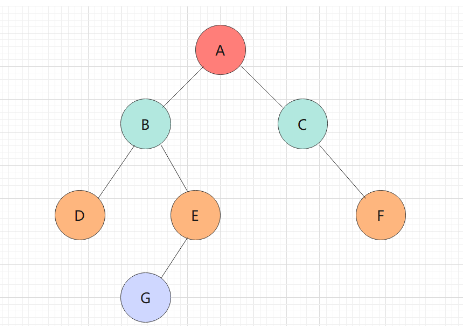
先序

中序

先序遍历是根节点、左子树、右子树。中序遍历是左子树、根节点、右子树

思路

根据先序遍历得到根节点，然后在中序遍历中，根据根节点的值找到index，把整个中序序列一分为二，左侧是左子树，右侧是右子树，这样去递归就可以了。

先序遍历数组的起始位置判断：

在每个左子树的递归中，下一轮的根节点显然是prestart + 1 (因为最初prestart是0，这时候已经用过了)，所以先序遍历左子树的起点是prestart + 1，左子树的终点下标应该是先序遍历所能访问到的左子树的最后一个节点的下标，也就是要在prestart的基础上加上左子树的结点数，即preStart + nums_of_left_tree

在每个右子树的递归中，下一轮的根节点显然是左子树范围内的右侧的全部，即preStart + nums_of_left_tree + 1，右子树的终点下标是preEnd。

注：nums_of_left_tree是通过index（当前中序遍历根节点坐标）减去当前中序遍历的初始结点坐标得到的

原因：中序遍历的根节点坐标将整个树左右分为左子树和右子树，根节点左侧的全部结点都是左子树的结点，因此index-instart得到的就是左子树的结点数

中序遍历数组的起始位置判断：

先搞清楚先序遍历数组的起始位置，再考虑中序的就很简单了，已经得到了index（当前中序遍历的根结点坐标），index左侧的都是左子树，右侧都是右子树

因此，左子树的递归中，初始位置为instart，终点位置为index-1

右子树的递归中，中序遍历数组初始位置为index+1，终点位置为inend

完整代码

public TreeNode buildTree(int[] preorder, int[] inorder) {
        return bulid(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);//这个先写，你传入的参数肯定就是这几个
    }

    public TreeNode bulid(int[] preorder, int preStart, int preEnd, int[] inorder, int inStart, int inEnd){
        //最后写递归出口 base case，很简单，就是两个数组之一越界就是出口（其实写1个也行，因为两个数组长度肯定相同的）
        if(preStart > preEnd || inStart > inEnd){
            return null;
        }

        /*先序遍历框架-根、左、右*/
        //1.先构造根节点的值，做根节点
        //2.递归构造左子树
        //3.递归构造右子树

        //1.很明显根节点的值由先序遍历数组的第一个值确定
        int rootVal = preorder[preStart];
        TreeNode root = new TreeNode(rootVal);
        //2.递归构造左子树
        // root.left = bulid(preorder, ?, ?, inorder, ?, ?);//？需要我们画图去求的，也就是左右子树的索引
        // root.right = bulid(preorder, ?, ?, inorder, ?, ?);//？需要我们画图去求的，也就是左右子树的索引
        //首先通过rootVal在inorder中的索引（index），然后就能够知道inorder中左子树和右子树的边界
        //可以改进的，一开始用hashMap把inorder的值和索引存好，到时候直接查就行。
        int index = -1;
        for(int i = inStart; i <= inEnd; i++){
            if(rootVal == inorder[i]){
                index = i;
                break;
            }
        }
        //找到了index，确定inorder中左右子树的边界
        // root.left = bulid(preorder, ?, ?, inorder, inStart, index - 1);//确定inorder中左子树的边界
        // root.right = bulid(preorder, ?, ?, inorder, index + 1, inEnd);//确定inorder中右子树的边界
        //通过inorder中左子树节点的数目来确定preorder中左右子树的边界
        int nums_of_left_tree = index - inStart; 
        // root.left = bulid(preorder, preStart + 1, preStart + nums_of_left_tree, inorder, ?, ?);//确定preorder中左子树的边界
        // root.right = bulid(preorder, preStart + nums_of_left_tree + 1, preEnd, inorder, ?, ?);//确定preorder中右子树的边界
        //最终确认好preorder和inorder中的左右子树边界
        root.left = bulid(preorder, preStart + 1, preStart + nums_of_left_tree, inorder, inStart, index - 1);
        root.right = bulid(preorder, preStart + nums_of_left_tree + 1, preEnd, inorder, index + 1, inEnd);
        return root;
    }

欢迎在评论区指出错误、交流题目