蓝桥杯备赛 day 2 —— 二分算法（C/C++，零基础，配图）

目录

🌈前言：

📁 二分的概念

📁 整数二分

📁 二分的模板

📁 习题

📁 总结

---

🌈前言：

????????这篇文章主要是准备蓝桥杯竞赛同学所写，为你更好准备蓝桥杯比赛涉及的算法知识点。不知道你是否苦恼于不知算法从何学起，苦恼于网上资料稀少，或者复杂难懂，这篇文章就是帮助这部分同学的。

? ? ? ? 下面整理了蓝桥杯考点大纲：

???????????????蓝桥杯考点大纲

??

? ? ? ? 通过上图，我们知道二分在蓝桥杯比赛中也是比较重要的，所以我们这里就单独写了一篇文章介绍，不仅是因为比较重要，而且二分算法对于刚接触算法的人来说比较复杂，易错点较多，需要不断调试。

📁 二分的概念

? ? ? ? 二分，字面意思就是通过判断是否满足条件将区间分成两份。通常的比如大于等于 或者? 小于等于.......

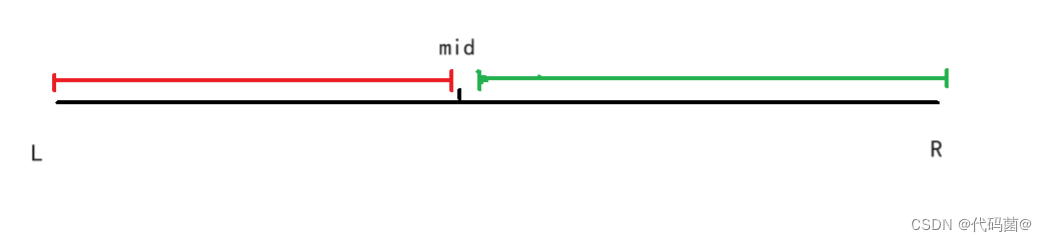
📁 整数二分

? ? ? ? 对于整数二分，我们可以分成两中类型 ：

? ? ? ? 1. [L ，Mid - 1] 和 [Mid , R] ：所求答案在Mid 右边

? ? ? ? 2. [L , Mid ] 和 [Mid + 1 , R] ：所求答案在Midz左边

? ? ? ? 这两种不同类型的区间，是由于判断条件不同形成的。

📁 二分的模板

? ? ? ? 为了大家更好的做题，已经比赛中更好的利用时间，这里提供了整数二分的模板，以及浮点数二分的模板。

1) 区间[L , R] 划分成[L,Mid] 和 [Mid+1 , R]
bool check(int x)
{
    ...    //检查x是否满足某种条件
}
int bearch_1(int l,int r)
{
    while(l < r)
    {
        int mid = (l + r ) / 2;
        if(check(mid))
            r = mid;
        else
            l = mid + 1;
    }
    return 1;
}

2) 区间[L , R] 划分成[L,Mid-1] 和 [Mid , R]
bool check(int x)
{
    ...    //检查x是否满足某种条件
}
int bearch_2(int l,int r)
{
    while(l < r)
    {
        int mid = (l + r + 1 ) / 2;
        if(check(mid))
            l = mid;
        else
            r = mid - 1;
    }
    return 1;
}

? ? ? ? 对于浮点数二分，并不需要关注+-1的问题，所以相对于整数二分来说，简单一些。当然一般来说，对于浮点数二分，我们需要保证精确度在1e-6（1的-6次方）。

bool check((int x)
{
    ...    //检查x是否满足条件
}

int bearch_1(int l,int r)
{
    while(r - l > 1e-6 )
    {
        int mid = (l + r ) / 2;
        if(check(mid))
            r = mid;
        else
            l = mid ;
    }
    return 1;
}

📁 习题

1. 数的范围?789. 数的范围 - AcWing题库

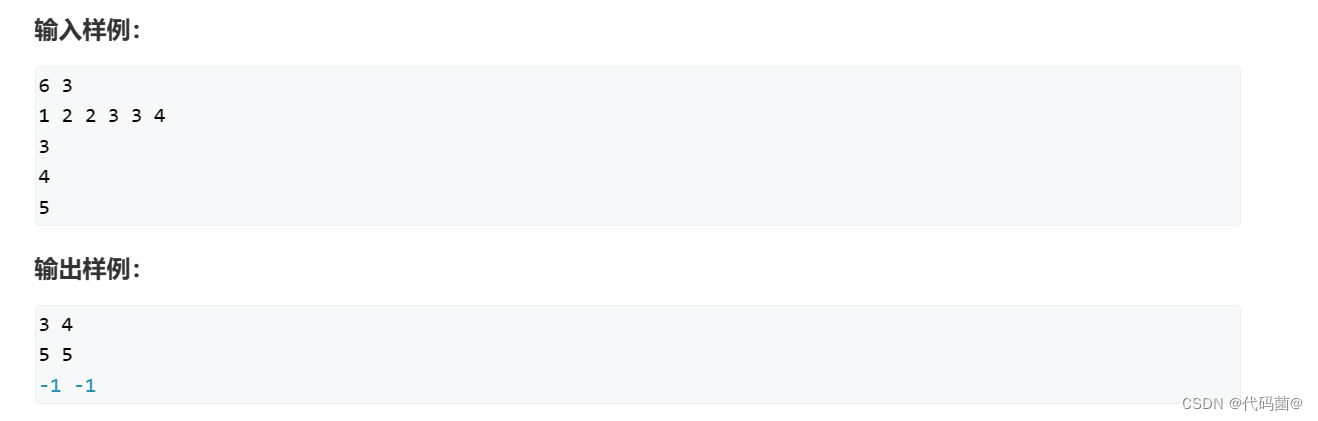
? ? ? ? 这道题其实就是一道非常经典的二分题目，首先我们找出左边第一次出现的x,再找出右边第一次出现的x，如果没有找到，则输出-1 -1。

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 100010;

int q[N];
int n,m;


int main()
{
    
    cin >> n>>m;
    for(int i=0;i<n;i++)
        cin>>q[i];
    
    while(m--)
    {
        int x;
        cin>>x;
        int l = 0;
        int r = n-1;
        while(l < r)
        {
            int mid = (l + r) >> 1;
            if(q[mid] >= x)
                r = mid;
            else
                l = mid + 1;
        }
        if(q[l] != x)
            printf("-1 -1\n");
        else
        {
            printf("%d ",l);
            r = n-1;
            while(l < r)
            {
                int mid = (l + r + 1) >> 1;
                if(q[mid] <= x)
                    l = mid;
                else
                    r = mid -1;
            }
            printf("%d\n",l);
        }
    }
    return 0;
}

2.数的三次方根?790. 数的三次方根 - AcWing题库

? ? ? ? 我们从数据范围当做区间，通过二分找出浮点数n的三次方根。

#include <iostream>
#include <cstdio>

using namespace std;

int main()
{
    double x ;
    cin >> x;
    double l = -10000,r =10000;
    while(r -l > 1e-8)
    {
        double m = (r + l) /2;
        if(m * m * m >= x)
            r = m;
        else
            l = m;
    }
    printf("%lf",l);
    return 0;
}

📁 总结

? ? 以上，我们就对二分在蓝桥杯中的知识点进行了讲解，并针对性的讲解了例题，当然这也只是帮你更好的理解这些算法知识，想要学好算法，还需要不断地刷题练习，这里推荐到洛谷，acwing等网站进行练习，比如你看完了这篇文章，做回了例题习题，就可以上这些网站进行想应的练习。