每周一算法:倍增法查找位置
倍增法
倍增法(Binary Lifting),顾名思义,就是利用“以翻倍的速度增长”的思想来解决问题的一类算法。
下面介绍如何使用倍增法在有序的序列中查找满足条件的位置。
题目描述
给定一个单调不降的序列,以及 m m m个查询,每个查询是一个数字 k k k,查找第一个大于等于 k k k的位置。
输入格式
第一行 n n n 和 m m m;
第二行 n n n 个元素的序列;
第三行 m m m 个数字,表示 m m m 个查询的 k k k, 每个查询的 k k k,确保在序列的最大值范围内。
输出格式
m m m 个数字,表示第一个大于等于 k k k 的位置,用空格隔开。
样例输入
10 1
1 2 3 4 6 6 6 8 9 10
6
样例输出
5
数据范围
- 20%的数据, 1 ≤ n , m ≤ 1000 1\le n,m\le 1000 1≤n,m≤1000
- 100%的数据, 1 ≤ n , m ≤ 1 0 5 1\le n,m\le 10^5 1≤n,m≤105, 1 ≤ 1\le 1≤所有元素 ≤ 1 0 9 \le 10^9 ≤109,所有 1 ≤ k ≤ 1\le k \le 1≤k≤序列最大值
算法思想
在单调不降的序列中查找一个大于等于 k k k 的位置,朴素的做法是从位置 1 1 1开始判断,不满足要求则每次向右移动 1 1 1个位置,重复进行直到找到满足条件的位置,时间复杂度为 O ( n ) O(n) O(n)。
倍增法也从位置 1 1 1开始判断,如果该位置上的数小于 k k k,则将移动的距离增加 1 1 1倍,然后向右移动;否则,如果该位置上的数大于等于 k k k,则将移动的距离减半,继续判断。重复进行直到不能移动为止,时间复杂度为 O ( l o g n ) O(logn) O(logn)。
移动过程如下图所示:
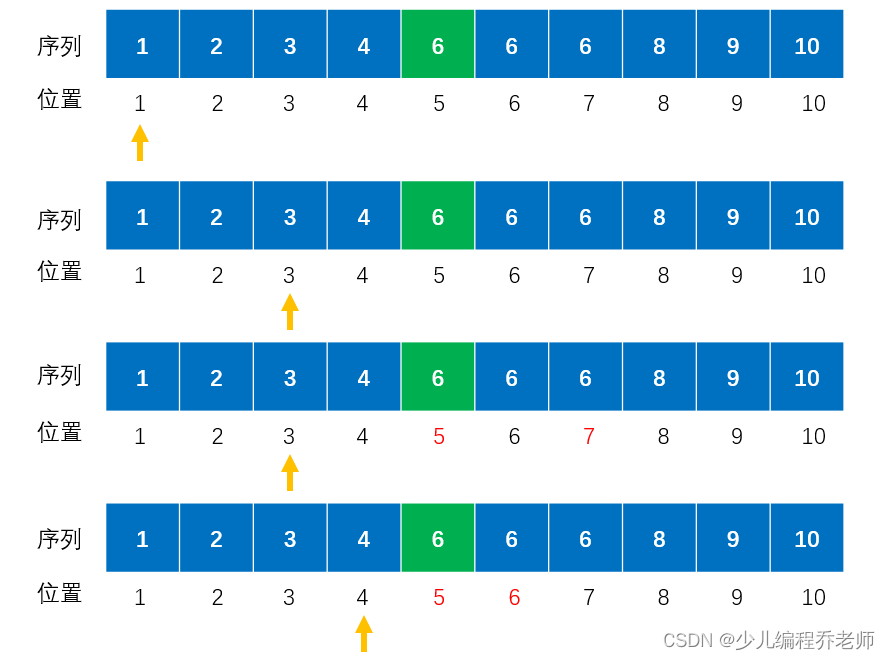
查找结束后会停留在最后一个小于
k
k
k的位置上。
代码实现
#include <iostream>
using namespace std;
const int N = 5e5 + 10;
int a[N];
int main()
{
int n, m, k;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i ++) scanf("%d", a + i);
while(m --) {
scanf("%d", &k);
//x表示位置,p表示增加距离
int x = 0, p = 1;
while(p != 0) {
//x位置上的数小于k,则将移动的距离增加1倍
if(x + p <= n && a[x + p] < k) {
x += p;
p *= 2;
}
//x位置上的数大于等于k,则将移动的距离减半
else p /= 2;
}
//x最终停留在最后一个小于k的位置上,应输出x + 1
printf("%d ", x + 1);
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- MySQL中的JSON数据类型计数及多张表COUNT的数据相加
- 这30个人工智能工具我打赌你一定不知道
- 基于SSM的教育管理系统
- 分享一款超级无滴好用的eclipse代码自动提示补全插件
- 构建现代网络教育系统的技术实践
- C++折半插入排序详解以及代码实现
- Speculative Oracles on Memory Tagging
- 网站安全每日话题——网页内容被篡改怎么办
- 赛氪受邀参加安徽省翻译协会2023年年会
- UE5.1_Python使用1