C++ AVL树
目录
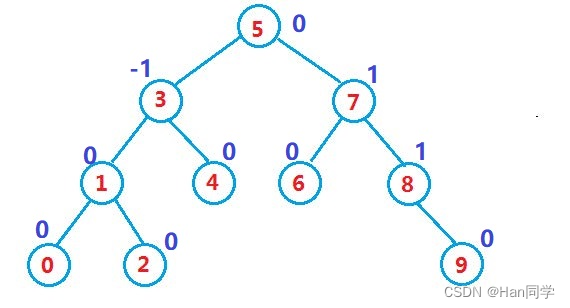
一、概念
二叉搜索树的效率可以通过AVL树进行改善。AVL树是由两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明的一种数据结构,用于解决二叉搜索树在数据有序或接近有序时退化为单支树的问题。
AVL树具有以下性质:
- AVL树要么是空树,要么是具有以下性质的二叉搜索树。
- 它的左右子树都是AVL树。
- 左右子树高度之差(平衡因子)的绝对值不超过1(-1/0/1)。
为了保持AVL树的平衡,当向树中插入新节点后,可能需要对树进行调整。这些调整操作包括旋转和重新计算节点的高度。
通过保持平衡因子的绝对值不超过1,AVL树可以降低树的高度,从而减少平均搜索长度,提高查找效率。这使得AVL树成为一种高效的数据结构,适用于需要频繁插入和查找操作的场景。
二、实现AVL树
1、AVL树节点的定义
template<class K,class V>
struct AVLTreeNode
{
AVLTreeNode<K, V>* _left;//左节点
AVLTreeNode<K, V>* _right;//右节点
AVLTreeNode<K, V>* _parent;//父节点
pair<K, V> _kv;
int _bf; // 平衡因子
AVLTreeNode(const pair<K, V>& kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(kv)
, _bf(0)
{}
};2、插入
template<class K,class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr) {
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (cur->_kv.first < kv.first) {
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first) {
parent = cur;
cur = cur->_left;
}
else {
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first > kv.first) {
parent->_left = cur;
}
else {
parent->_right = cur;
}
cur->_parent = parent;
// 更新平衡因子
return true;
}
private:
Node* _root = nullptr;
};-
首先,我们检查根节点?
_root?是否为空。如果为空,表示树为空,我们直接将新节点作为根节点插入,并返回 true。 -
如果根节点不为空,我们需要找到合适的位置来插入新节点。我们使用两个指针?
parent?和?cur?来追踪当前节点和其父节点。开始时,它们都指向根节点。 -
进入一个循环,直到找到合适的插入位置或者发现已经存在相同的键。在循环中,我们比较当前节点的键和要插入的键的大小关系,根据比较结果更新?
parent?和?cur?的值。 -
如果当前节点的键小于要插入的键,表示要插入的键应该在当前节点的右子树中,我们更新?
parent?和?cur?分别为当前节点和其右子节点。 -
如果当前节点的键大于要插入的键,表示要插入的键应该在当前节点的左子树中,我们更新?
parent?和?cur?分别为当前节点和其左子节点。 -
如果当前节点的键等于要插入的键,表示已经存在相同的键,无法插入,返回 false。
-
当找到合适的插入位置后,我们创建一个新的节点?
cur,并将要插入的键值对?kv?存储在新节点中。 -
根据?
parent?和?cur?的键的大小关系,将新节点插入到正确的位置。如果?parent?的键大于要插入的键,将新节点作为?parent?的左子节点;否则,将新节点作为?parent?的右子节点。 -
最后,我们需要更新 AVL 树的平衡因子,以确保树的平衡性。
-
函数返回 true,表示插入成功。
3、更新平衡因子
在 AVL 树中,平衡因子是用来衡量节点的左子树和右子树的高度差的指标。当插入或删除节点后,可能会导致某些节点的平衡因子不再满足 AVL 树的平衡条件(平衡因子的绝对值不超过1)。因此,需要更新节点的平衡因子以恢复树的平衡性。
在 AVL 树中,更新平衡因子有:左单旋、右单旋、左右双旋(先左后右、先右后左)四种形式。
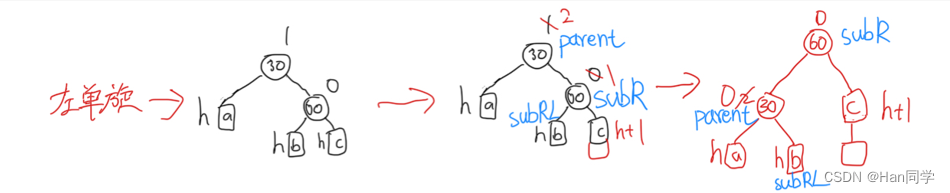
左单旋
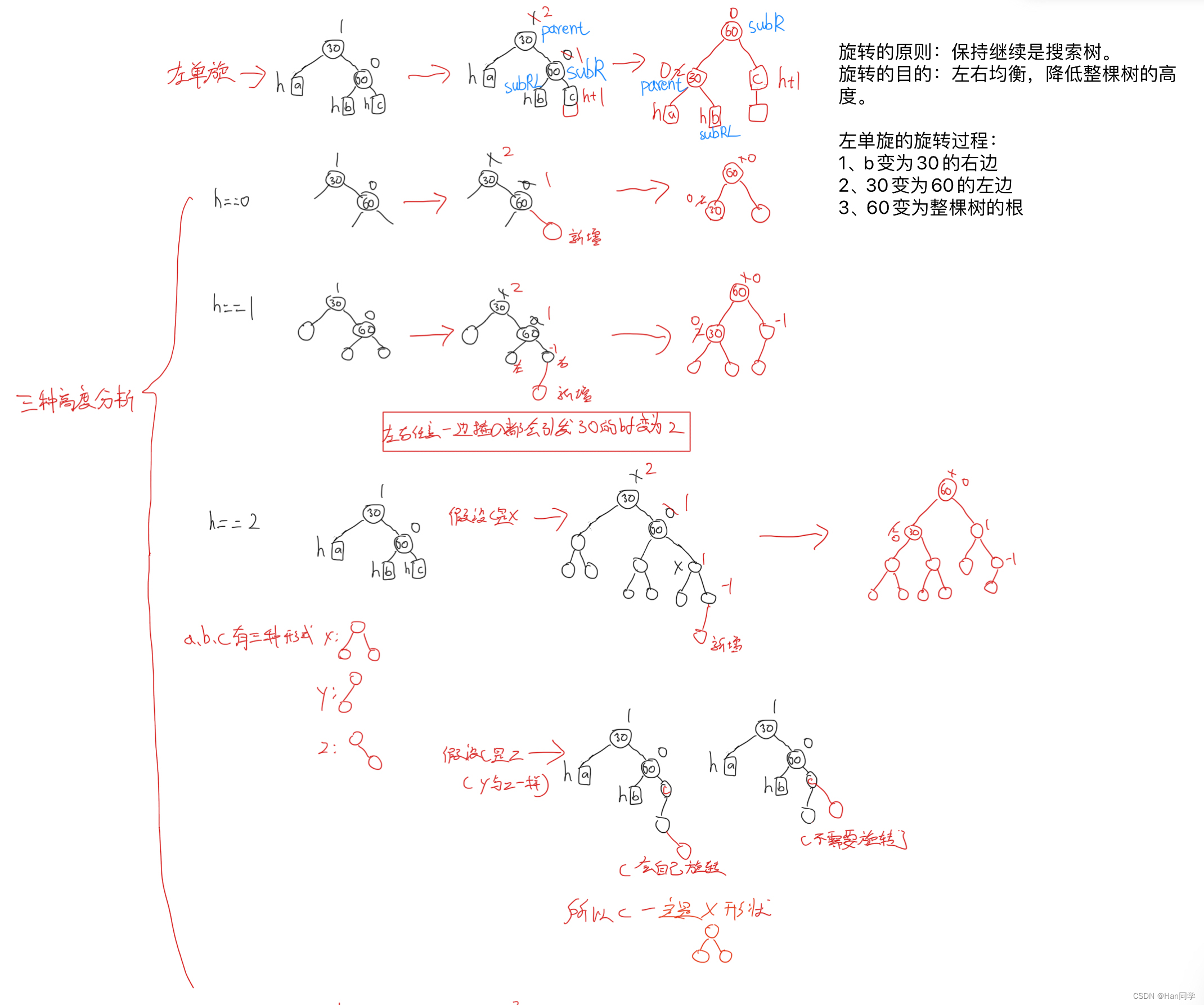
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* ppnode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (ppnode == nullptr) {
_root = subR;
_root->_parent = nullptr;
}
else {
if (ppnode->_left == nullptr) {
ppnode->_left = subR;
}
else {
ppnode->_right = subR;
}
subR->_parent = ppnode;
}
parent->_bf = subR->_bf = 0;
}
-
首先,我们定义了三个指针变量:
subR?指向父节点的右子节点,subRL?指向?subR?的左子节点,ppnode?指向父节点的父节点。 -
我们将父节点的右子节点指向?
subRL,这样父节点和?subR?就断开了连接。如果?subRL?不为空,我们还需要将其父节点指针指向父节点。 -
接下来,我们将父节点的父节点指针指向?
subR,将?subR?的左子节点指向父节点。 -
如果父节点的父节点指针?
ppnode?为空,表示父节点是根节点,我们将根节点指针?_root?指向?subR,并将根节点的父节点指针置为空。 -
如果父节点的父节点指针?
ppnode?不为空,我们需要根据父节点在其父节点的位置来更新指、针。如果父节点是其父节点的左子节点,我们将?subR?设置为其父节点的左子节点;否则,将?subR?设置为其父节点的右子节点。同时,我们还需要更新?subR?的父节点指针为?ppnode。 -
最后,我们将父节点和?
subR?的平衡因子都设置为 0,表示它们的高度相等。
右单旋

void RotateR(Node* parent)
{
Node* subL = parent_ > _left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* ppnode = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (parent == _root) {
_root = subL;
_root->_parent = nullptr;
}
else {
if (ppnode->_left == parent) {
ppnode->_left = subL;
}
else {
ppnode->_right = subL;
}
subL->_parent
}
subL->_bf = parent->_bf = 0;
}-
首先,我们定义了三个指针变量:
subL?指向父节点的左子节点,subLR?指向?subL?的右子节点,ppnode?指向父节点的父节点。 -
我们将父节点的左子节点指向?
subLR,这样父节点和?subL?就断开了连接。如果?subLR?不为空,我们还需要将其父节点指针指向父节点。 -
接下来,我们将父节点的父节点指针指向?
subL,将?subL?的右子节点指向父节点,以完成右旋转操作。 -
如果父节点是根节点?
_root,我们将根节点指针?_root?指向?subL,并将根节点的父节点指针置为空。 -
如果父节点的父节点指针?
ppnode?不为空,我们需要根据父节点在其父节点的位置来更新指针。如果父节点是其父节点的左子节点,我们将?subL?设置为其父节点的左子节点;否则,将?subL?设置为其父节点的右子节点。同时,我们还需要更新?subL?的父节点指针为?ppnode。 -
最后,我们将父节点和?
subL?的平衡因子都设置为 0,表示它们的高度相等。
左右双旋—先左旋再右旋
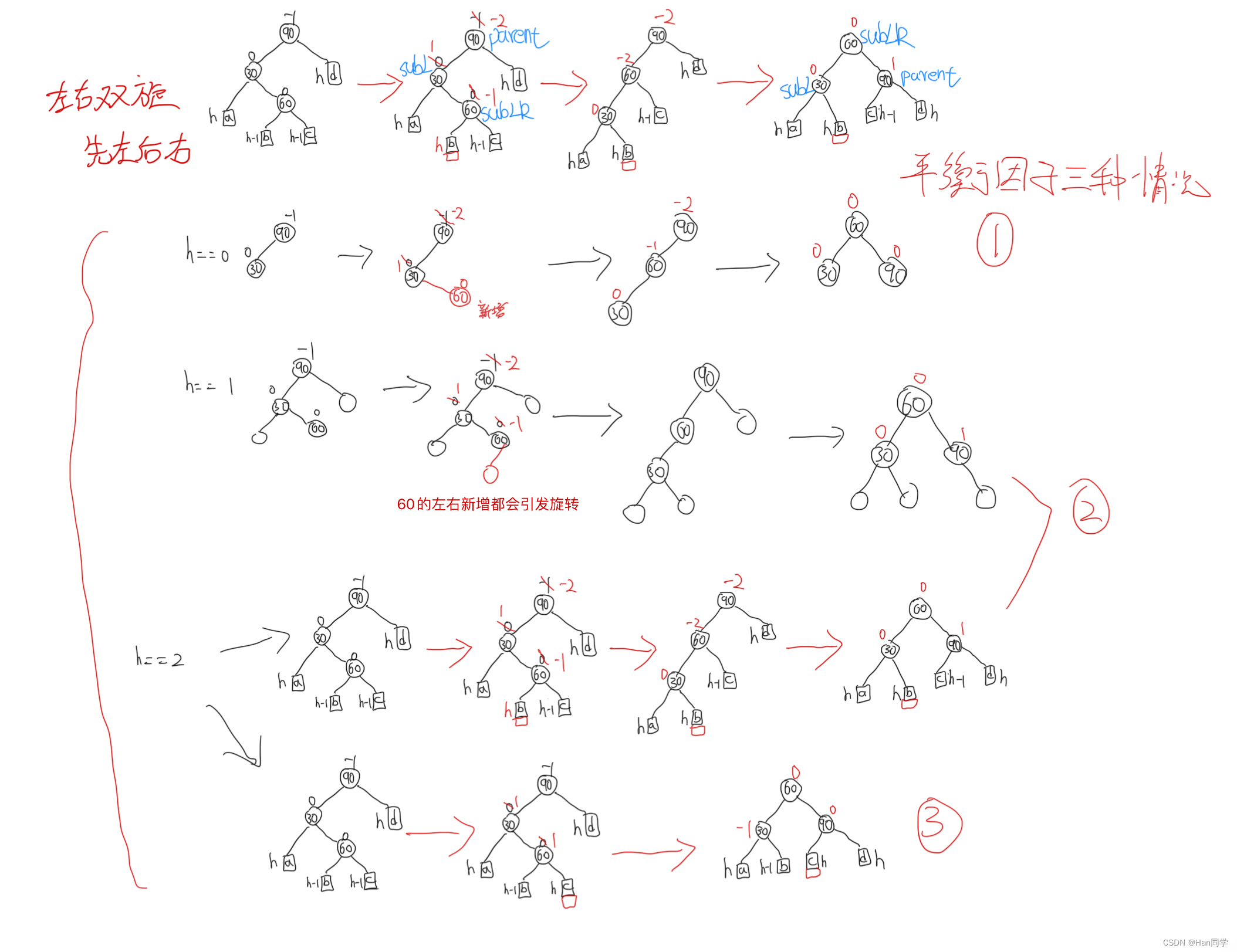
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == 1) {
parent->_bf = 0;
subLR->_bf = 0;
subL->_bf = -1;
}
else if (bf == -1){
parent->_bf = 1;
subLR->_bf = 0;
subL->_bf = 0;
}
else if (bf == 0){
parent->_bf = 0;
subLR->_bf = 0;
subL->_bf = 0;
}
else{
assert(false);
}
}?
-
首先,我们定义了两个指针变量:
subL?指向父节点的左子节点,subLR?指向?subL?的右子节点,以及一个整数变量?bf?来保存?subLR?的平衡因子。 -
我们先进行左旋转操作,调用?
RotateL?函数,将父节点的左子树进行左旋转。 -
然后,再进行右旋转操作,调用?
RotateR?函数,将父节点进行右旋转。 -
接下来,根据?
subLR?的平衡因子?bf?的值,更新父节点、subLR?和?subL?的平衡因子。-
如果?
bf?的值为 1,表示?subLR?的左子树高度大于右子树高度,需要进行左高旋转。此时,将父节点的平衡因子设为 0,subLR?的平衡因子设为 0,subL?的平衡因子设为 -1。 -
如果?
bf?的值为 -1,表示?subLR?的左子树高度小于右子树高度,需要进行右高旋转。此时,将父节点的平衡因子设为 1,subLR?的平衡因子设为 0,subL?的平衡因子设为 0。 -
如果?
bf?的值为 0,表示?subLR?的左子树和右子树高度相等,不需要进行旋转。此时,将父节点、subLR?和?subL?的平衡因子都设为 0。 -
如果?
bf?的值不是 1、-1 或 0,表示出现了错误的平衡因子,使用?assert(false)?断言来报错。
-
右左双选—先右旋再左旋
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 1)
{
subR->_bf = 0;
parent->_bf = -1;
subRL->_bf = 0;
}
else if (bf == -1)
{
subR->_bf = 1;
parent->_bf = 0;
subRL->_bf = 0;
}
else if (bf == 0)
{
subR->_bf = 0;
parent->_bf = 0;
subRL->_bf = 0;
}
else
{
assert(false);
}
}
-
首先,我们定义了两个指针变量:
subR?指向父节点的右子节点,subRL?指向?subR?的左子节点,以及一个整数变量?bf?来保存?subRL?的平衡因子。 -
我们先进行右旋转操作,调用?
RotateR?函数,将父节点的右子树进行右旋转。 -
然后,再进行左旋转操作,调用?
RotateL?函数,将父节点进行左旋转。 -
接下来,根据?
subRL?的平衡因子?bf?的值,更新父节点、subR?和?subRL?的平衡因子。-
如果?
bf?的值为 1,表示?subRL?的左子树高度大于右子树高度,需要进行左高旋转。此时,将?subR?的平衡因子设为 0,父节点的平衡因子设为 -1,subRL?的平衡因子设为 0。 -
如果?
bf?的值为 -1,表示?subRL?的左子树高度小于右子树高度,需要进行右高旋转。此时,将?subR?的平衡因子设为 1,父节点的平衡因子设为 0,subRL?的平衡因子设为 0。 -
如果?
bf?的值为 0,表示?subRL?的左子树和右子树高度相等,不需要进行旋转。此时,将?subR、父节点和?subRL?的平衡因子都设为 0。 -
如果?
bf?的值不是 1、-1 或 0,表示出现了错误的平衡因子,使用?assert(false)?断言来报错。
-
4、更新插入函数
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr) {
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (cur->_kv.first < kv.first) {
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first) {
parent = cur;
cur = cur->_left;
}
else {
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first > kv.first) {
parent->_left = cur;
}
else {
parent->_right = cur;
}
cur->_parent = parent;
// 更新平衡因子
while (parent) {
if (cur == parent->_right) {
parent->_bf++;
}
else {
parent-> _bf--;
}
if (parent->_bf == 1 || parent->_bf == -1) {
parent = parent->_parent;
cur = cur->_parent;
}
else if (parent->_bf == 0) {
break;
}
else if(parent->_bf == 2 || parent->_bf == -2){
if (parent->_bf == 2 && cur->_bf == 1){
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1){
RotateR(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent);
}
else
{
assert(false);
}
break;
}
else {
assert(false);
}
}
return true;
}在插入节点后,通过循环更新节点的平衡因子以保持 AVL 树的平衡性。平衡因子更新的实现过程:
-
首先,我们进入一个循环,该循环的目的是从插入节点的父节点开始,向上更新平衡因子直到根节点。
-
在循环中,我们根据插入节点?
cur?在父节点?parent?的左子树还是右子树中进行判断。 -
如果?
cur?是?parent?的右子节点,表示插入节点在右子树中,我们将?parent?的平衡因子?_bf?加1。 -
如果?
cur?是?parent?的左子节点,表示插入节点在左子树中,我们将?parent?的平衡因子?_bf?减1。 -
然后,我们检查?
parent?的平衡因子?_bf?的值,根据不同的情况进行处理:-
如果?
parent?的平衡因子?_bf?的值为 1 或 -1,表示?parent?的平衡因子仍然满足 AVL 树的平衡条件,我们继续向上更新。 -
如果?
parent?的平衡因子?_bf?的值为 0,表示?parent?的平衡因子不再发生变化,我们可以停止向上更新。 -
如果?
parent?的平衡因子?_bf?的值为 2 或 -2,也就是说,当?parent?的左子树和右子树的高度差超过 1 时,需要进行相应的平衡调整操作。具体的操作取决于?parent?和?cur(当前插入的节点)的平衡因子。 -
如果?
parent?的平衡因子?_bf?为 2,表示左子树高度较高,需要进行旋转操作。-
如果?
cur?的平衡因子?_bf?为 1,表示?cur?是?parent?的左子节点的左子节点,也就是说,新插入的节点在?parent?的左子树的左侧,这种情况下,可以通过一次左旋转操作?RotateL(parent)?来恢复平衡。 -
如果?
cur?的平衡因子?_bf?为 -1,表示?cur?是?parent?的左子节点的右子节点,也就是说,新插入的节点在?parent?的左子树的右侧,这种情况下,需要进行右左旋转操作?RotateRL(parent)?来恢复平衡。
-
-
如果?
parent?的平衡因子?_bf?为 -2,表示右子树高度较高,需要进行旋转操作。-
如果?
cur?的平衡因子?_bf?为 -1,表示?cur?是?parent?的右子节点的右子节点,也就是说,新插入的节点在?parent?的右子树的右侧,这种情况下,可以通过一次右旋转操作?RotateR(parent)?来恢复平衡。 -
如果?
cur?的平衡因子?_bf?为 1,表示?cur?是?parent?的右子节点的左子节点,也就是说,新插入的节点在?parent?的右子树的左侧,这种情况下,需要进行左右旋转操作?RotateLR(parent)?来恢复平衡。
-
-
如果 parent 和 cur 的平衡因子 _bf 不满足上述任何一种情况,那么就会触发 assert(false),这是一个断言,表示程序遇到了不应该出现的情况,会导致程序终止。
-
-
在这段代码中,第二个?
break?语句的作用是跳出?while?循环。当?
parent?节点的平衡因子?_bf?的绝对值达到 2 时,表示树的平衡被打破,需要进行旋转操作来恢复平衡。在进行了相应的旋转操作后,就不需要继续向上更新平衡因子了,因为旋转操作已经恢复了树的平衡性。因此,执行?
break?语句来跳出?while?循环,结束平衡因子的更新过程。 -
最后,跳出循环并返回 true,表示插入成功。
5、中序遍历
public:
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_kv.first << " ";
_InOrder(root->_right);
}-
InOrder?函数:这是一个中序遍历函数,用于按照中序遍历的顺序打印出树中的所有节点。它调用了私有函数?_InOrder?来进行递归遍历。 -
_InOrder?函数:这是一个私有的中序遍历函数,用于递归地遍历树中的节点。如果当前节点为空,直接返回;否则,先遍历左子树,然后打印当前节点,最后遍历右子树。
6、检查平衡
public:
bool IsBalance()
{
return _IsBalance(_root);
}
private:
bool _IsBalance(Node* root)
{
if (root == nullptr)
return true;
int leftH = _Height(root->_left);
int rightH = _Height(root->_right);
if (rightH - leftH != root->_bf){
cout << root->_kv.first << "节点平衡因子异常" << endl;
return false;
}
return abs(rightH - leftH) < 2
&& _IsBalance(root->_left)
&& _IsBalance(root->_right);
}-
IsBalance?函数:这是一个检查树是否平衡的函数,用于检查树中的所有节点的平衡因子是否满足 AVL 树的平衡条件。它调用了私有函数?_IsBalance?来进行递归检查。 -
_IsBalance?函数:这是一个私有的检查节点是否平衡的函数,用于递归地检查节点的平衡因子。 -
如果当前节点为空,直接返回 true;否则,计算左子树和右子树的高度,检查高度差是否等于节点的平衡因子,如果不等于,打印错误信息并返回 false;
-
如果高度差的绝对值大于等于 2,或者左子树或右子树不平衡,返回 false;否则,返回 true。
7、获取树的高度
public:
int Height()
{
return _Height(_root);
}
private:
int _Height(Node* root)
{
if (root == nullptr)
return 0;
int leftH = _Height(root->_left);
int rightH = _Height(root->_right);
return leftH > rightH ? leftH + 1 : rightH + 1;
}-
Height?函数:这是一个获取树的高度的函数,用于计算树的高度。它调用了私有函数?_Height?来进行递归计算。 -
_Height?函数:这是一个私有的获取节点高度的函数,用于递归地计算节点的高度。如果当前节点为空,返回 0;否则,计算左子树和右子树的高度,返回较大的高度加 1。
三、测试+完整版代码
常规测试:
void Test_AVLTree1()
{
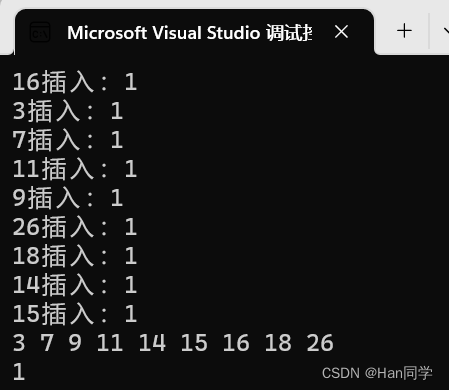
int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
AVLTree<int, int> t1;
for (auto e : a)
{
//可以使用这种方式帮助打断点查找错误
/* if (e == 14)
{
int x = 0;
}*/
t1.Insert(make_pair(e, e));
cout <<e<<"插入:"<<t1.IsBalance() << endl;
}
t1.InOrder();
cout << t1.IsBalance() << endl;
}
随机数测试:?
void Test_AVLTree2()
{
srand(time(0));
const size_t N = 5000000;
AVLTree<int, int> t;
for (size_t i = 0; i < N; ++i)
{
size_t x = rand() + i;
t.Insert(make_pair(x, x));
}
cout << t.IsBalance() << endl;
cout << t.Height() << endl;
}
?
完整版:?
#pragma once
#include <assert.h>
#include <iostream>
using namespace std;
template<class K,class V>
struct AVLTreeNode
{
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
pair<K, V> _kv;
int _bf; // balance factor
AVLTreeNode(const pair<K, V>& kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(kv)
, _bf(0)
{}
};
template<class K,class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr) {
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur) {
if (cur->_kv.first < kv.first) {
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first) {
parent = cur;
cur = cur->_left;
}
else {
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first > kv.first) {
parent->_left = cur;
}
else {
parent->_right = cur;
}
cur->_parent = parent;
// 更新平衡因子
while (parent) {
if (cur == parent->_right) {
parent->_bf++;
}
else {
parent-> _bf--;
}
if (parent->_bf == 1 || parent->_bf == -1) {
parent = parent->_parent;
cur = cur->_parent;
}
else if (parent->_bf == 0) {
break;
}
else if(parent->_bf == 2 || parent->_bf == -2){
if (parent->_bf == 2 && cur->_bf == 1){
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1){
RotateR(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent);
}
else
{
assert(false);
}
break;
}
else {
assert(false);
}
}
return true;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool IsBalance()
{
return _IsBalance(_root);
}
int Height()
{
return _Height(_root);
}
private:
int _Height(Node* root)
{
if (root == nullptr)
return 0;
int leftH = _Height(root->_left);
int rightH = _Height(root->_right);
return leftH > rightH ? leftH + 1 : rightH + 1;
}
bool _IsBalance(Node* root)
{
if (root == nullptr)
return true;
int leftH = _Height(root->_left);
int rightH = _Height(root->_right);
if (rightH - leftH != root->_bf){
cout << root->_kv.first << "节点平衡因子异常" << endl;
return false;
}
return abs(rightH - leftH) < 2
&& _IsBalance(root->_left)
&& _IsBalance(root->_right);
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_kv.first << " ";
_InOrder(root->_right);
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* ppnode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (ppnode == nullptr) {
_root = subR;
_root->_parent = nullptr;
}
else {
if (ppnode->_left == parent) {
ppnode->_left = subR;
}
else {
ppnode->_right = subR;
}
subR->_parent = ppnode;
}
parent->_bf = subR->_bf = 0;
}
void RotateR(Node* parent)
{
Node* subL = parent -> _left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* ppnode = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (parent == _root) {
_root = subL;
_root->_parent = nullptr;
}
else {
if (ppnode->_left == parent) {
ppnode->_left = subL;
}
else {
ppnode->_right = subL;
}
subL->_parent = ppnode;
}
subL->_bf = parent->_bf = 0;
}
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == 1) {
parent->_bf = 0;
subLR->_bf = 0;
subL->_bf = -1;
}
else if (bf == -1){
parent->_bf = 1;
subLR->_bf = 0;
subL->_bf = 0;
}
else if (bf == 0){
parent->_bf = 0;
subLR->_bf = 0;
subL->_bf = 0;
}
else{
assert(false);
}
}
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 1)
{
subR->_bf = 0;
parent->_bf = -1;
subRL->_bf = 0;
}
else if (bf == -1)
{
subR->_bf = 1;
parent->_bf = 0;
subRL->_bf = 0;
}
else if (bf == 0)
{
subR->_bf = 0;
parent->_bf = 0;
subRL->_bf = 0;
}
else
{
assert(false);
}
}
private:
Node* _root = nullptr;
};
void Test_AVLTree1()
{
int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
AVLTree<int, int> t1;
for (auto e : a)
{
//可以使用这种方式帮助打断点查找错误
/* if (e == 14)
{
int x = 0;
}*/
t1.Insert(make_pair(e, e));
cout <<e<<"插入:"<<t1.IsBalance() << endl;
}
t1.InOrder();
cout << t1.IsBalance() << endl;
}
void Test_AVLTree2()
{
srand(time(0));
const size_t N = 5000000;
AVLTree<int, int> t;
for (size_t i = 0; i < N; ++i)
{
size_t x = rand() + i;
t.Insert(make_pair(x, x));
}
cout << t.IsBalance() << endl;
cout << t.Height() << endl;
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- C++11 中的 emplace
- JS中call()、apply()、bind()改变this指向的原理
- End-to-End Object Detection with Transformers(2020)
- 【计算机网络】八股文 | 第二章
- 关于Smartbi登录代码逻辑漏洞的动态情报
- (赠源码)java+SpringBoot+mysql车辆故障报修系统26719-计算机毕业设计项目选题推荐
- 跨境电商如何开数百个账号窗口?多窗口同步功能了解一下!
- WinForm中使用MaskedTextBox制作IP地址输入框
- 多协议数据库Navicat Premium中文
- brew 安装使用 mysql、redis、mongodb
