数据结构学习 jz04二维矩阵找数字
发布时间:2023年12月17日
题目:

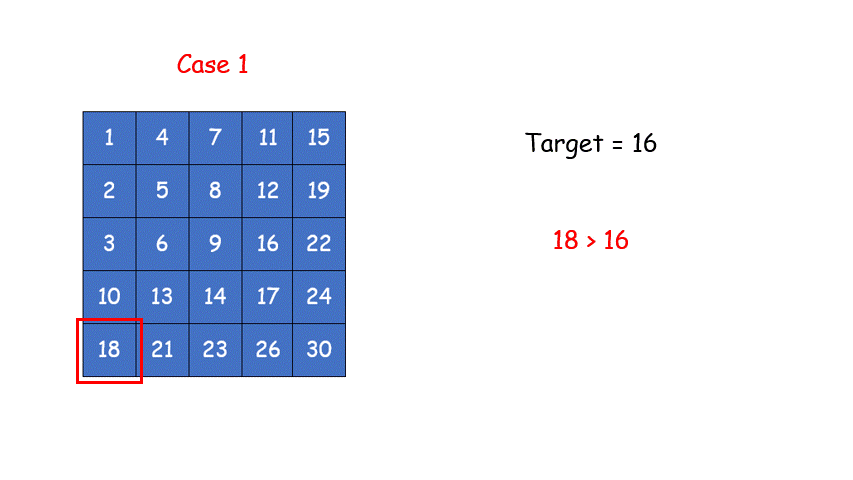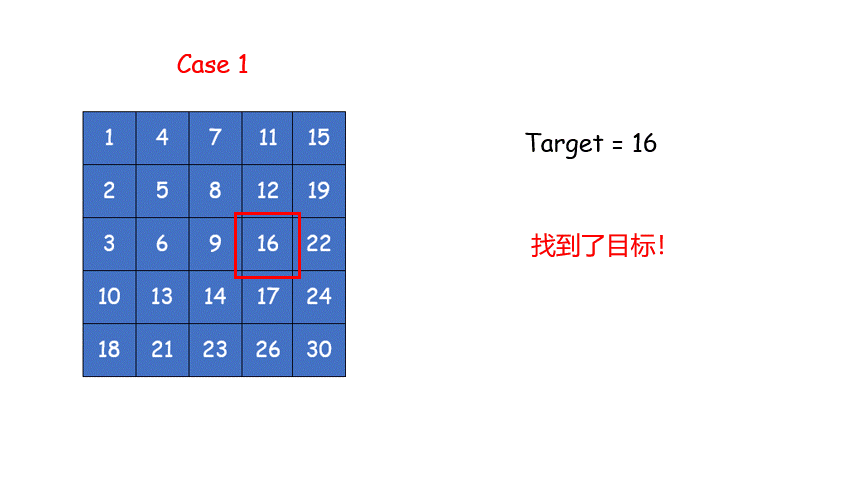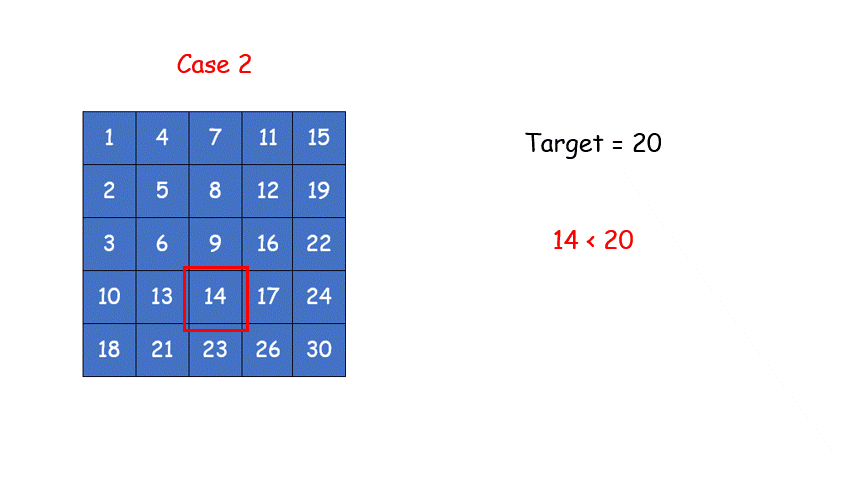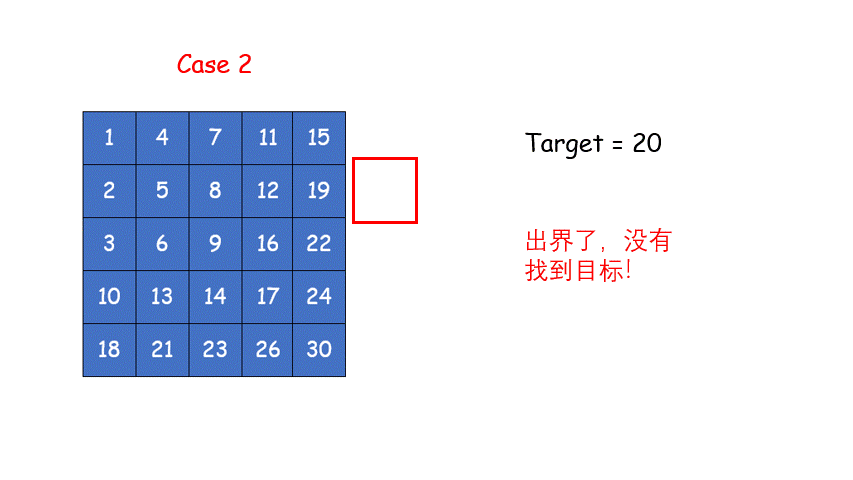
解法一:找角落点,然后渐进目标(像二叉搜索树)
时间复杂度O(n+m)
空间复杂度O(1)
#include <vector>
#include <iostream>
//解法一 找到角落的一个点,然后渐进目标
class Solution {
public:
bool findTargetIn2DPlants(std::vector<std::vector<int>>& plants, int target) {
if (plants.size() == 0 || plants[0].size() == 0) return false;//防止是空的
int m = plants[0].size();
int n = plants.size();
for (int x = 0, y = n-1; y >= 0 && x < m;)//从左下角向中心找目标点,要是找出界还没找到就返回false
{
if (plants[y][x] == target)//找到啦
return true;
else if (plants[y][x] > target)
y--;
else
x++;
}
return false;
}
};
void Test_solution1()
{
//std::vector<std::vector<int>> x{ {2, 3, 6, 8},{4, 5, 8, 9},{5, 9, 10, 12} };
std::vector<std::vector<int>> x{ {-5} };
int target = -2;
Solution solu;
std::cout << solu.findTargetIn2DPlants(x, target) << std::endl;
}解法二:二分查找
在对角线上迭代,对于每一个对角线元素,对该元素所在的行和列使用二分搜索
时间复杂度O(logk!) k=max{m,n}
空间复杂度O(1)

#include <iostream>
#include <vector>
//二分查找
//故意不写成递归是希望多锻炼一下直接写成循环的能力
class Solution {
public:
bool findTargetIn2DPlants(std::vector<std::vector<int>>& plants, int target) {
if (plants.empty() || plants[0].empty()) return false;
int m = plants[0].size()-1;
int n = plants.size()-1;
int row = 0;
int column = 0;
while (row <= n && column <= m)//在对角线上迭代,对于每一个对角线元素,对该元素所在的行和列使用二分搜索
{
//在行上使用二分查找
int up = row;
int down = n;
while (up <= down)
{
int mid_row = (up + down) / 2;
if (plants[mid_row][column] > target)
{
down = mid_row - 1;
}
else if (plants[mid_row][column] < target)
{
up = mid_row + 1;
}
else
{
return true;
}
}
//在列上使用二分查找
int left = column;
int right = m;
while (left <= right)
{
int mid_column = (left + right) / 2;
if (plants[row][mid_column] > target)
{
right = mid_column - 1;
}
else if (plants[row][mid_column] < target)
{
left = mid_column + 1;
}
else
{
return true;
}
}
++row;
++column;
}
return false;
}
};解法三:递归,在列上二分查找,在行上遍历
递归。
在列上用二分法,在行上遍历所有。
- 先在mid列上找到plants[row][mid] < target =< lants[row+1][mid]的行row
- 然后排除找到的行列的交点的左上(一定比目标小)和右下(一定比目标大)
- 接着分成右上和左下,分别调用函数进行递归
时间复杂度O(nlogm)
空间复杂度O(1)
#include <iostream>
#include <vector>
//解法三,递归 在列上用二分法,在行上遍历所有 先在mid列上找到plants[row][mid] < target =< lants[row+1][mid]的行row
//然后排除找到的行列的交点的左上(一定比目标小)和右下(一定比目标大)
//接着分成右上和左下,分别调用函数进行递归
class Solution {
public:
bool findTargetIn2DPlants(std::vector<std::vector<int>>& plants, int target) {
if (plants.size() == 0 || plants[0].size() == 0) return false;
int right = plants[0].size() - 1;
int down = plants.size() - 1;
return search_target(plants, target, 0, down, 0, right);
}
bool search_target(std::vector<std::vector<int>>& plants, int target, int up, int down, int left, int right)
{
if (left > right || up > down) return false;//找不到,超出范围
int mid = (left + right) / 2;//二分 列
int row = 0;
while (plants[row][mid] < target && row < down) ++row;//找行
if (plants[row][mid] == target) return true;//找到了
//递归
//后一个row不能是row+1,不然过不了{ {1,3,5} }
//两边只要有一边找到即可
return search_target(plants, target, up, row, mid + 1, right) || search_target(plants, target, row, down, left, mid - 1);
}
};
void Test_solution3()
{
//std::vector<std::vector<int>> x{ {2, 3, 6, 8},{4, 5, 8, 9},{5, 9, 10, 12} };
std::vector<std::vector<int>> x{ {1,3,5} };
int target = 1;
Solution solu;
std::cout << solu.findTargetIn2DPlants(x, target) << std::endl;
}运行结果
二分查找非常快哦。。。。
文章来源:https://blog.csdn.net/rainssssss/article/details/134923643
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【Python 千题 —— 基础篇】句子首字母要大写
- 光伏汇流箱浪涌保护器应用方案
- centos 9下/proc/sys/vm目录下文件的说明和配置详解。
- 私有部署ELK,搭建自己的日志中心(四)-- kibana展示es的数据
- python-分享篇-代码雨
- JVM 类加载子系统
- TCP发送优化(ZeroWindow分析)
- 泊松分布与二项分布的可加性
- YOLOv8算法优化:解决YOLOv8无法打印计算量(GFLOPs)的问题点
- Python深度学习技术进阶篇|Transformer模型详解