LeetCode 刷题日志

1954. 收集足够苹果的最小花园周长

1954. 收集足够苹果的最小花园周长

难度： 中等

题目大意：

给你一个用无限二维网格表示的花园，每一个 整数坐标处都有一棵苹果树。整数坐标 (i, j) 处的苹果树有 |i| + |j| 个苹果。

你将会买下正中心坐标是 (0, 0) 的一块 正方形土地 ，且每条边都与两条坐标轴之一平行。

给你一个整数 neededApples ，请你返回土地的 最小周长 ，使得 至少 有 neededApples 个苹果在土地 里面或者边缘上。

• 1 <= neededApples <= 10^15

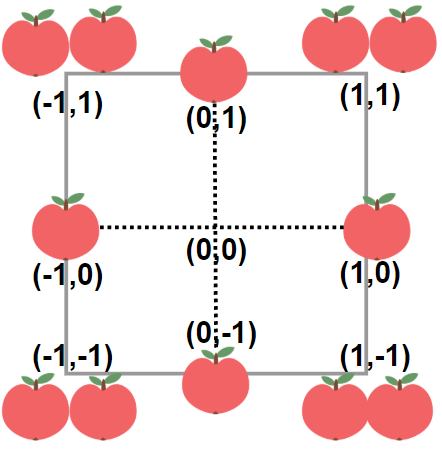
思考：

这个图形是很对称的，那么很自然会想到要推导一个用边长来表示边上的所有苹果数量，而且我们只需要计算出第一象限的苹果即可，假设最右边的的横坐标是x，那我们只需要计算(x, 0) 到 (x, x),然后根据对称性乘以4，然后对边长上的苹果求一个和

公式推导:
$$\sum _x^{2x}r=\frac{3x(x+1)}{2},边上苹果数=4?\sum _x^{2x}r=6x(x+1)=6(x^2+x)$$

$$\sum _0^n{r}^2=\frac{n(n+1)(2n+1)}{6}$$

$$\sum 苹果=\sum _0^{n}6(x^2+x)=2n(n+1)(2n+1)$$

就有了下面两种思路：

暴力枚举

我们至于要枚举边长，如果达到了要求，直接返回即可

代码实现

class Solution {
public:
    using LL = long long;
    long long minimumPerimeter(long long neededApples) {
        LL res = 0, sum = 0;
        for (int i = 0; ; i ++) {
            sum += 12 * (LL)i * i;
            if (sum >= neededApples) {
                res = i;
                break;
            }
        }
        return res * 8;
    }
};

考虑优化方案， 要满足2n(n + 1)(2n + 1) - k >= 0 我们画出这个图像

我们只需要求出与x正方向的交点即可，就有了下面这个思路

二分查找

注意到，在x0左侧的这一部分都是小于0的，在x0的右侧都是大于0的，这样就可以二分了

代码实现

class Solution {
public:
    using LL = long long;
    long long minimumPerimeter(long long neededApples) {;
        double l = 0, r = 70000;
        auto check = [&](double mid) -> bool {
            return 2 * mid * (mid + 1) * (2 * mid + 1) - neededApples < 0;
        };
        while (r - l > 1e-6) {
            double mid = (l + r) / 2;
            if (check(mid)) l = mid;
            else r = mid;
        }
        return ceil(l) * 8;
    }
};

• ceil(x)函数是对x上取整

【微语】做你自己，因为其他角色都已经有人扮演了。

结束了