[数据结构]顺序表

1、顺序表的概念及结构

1.1 线性表

线性表（ linear list ）是n个具有相同特性的数据元素的有限序列。 线性表是?种在实际中广泛使用的数据结构，常见的线性表：顺序表、链表、栈、队列、字符串...

线性表在逻辑上是线性结构，也就说是连续的?条直线。但是在物理结构上并不?定是连续的， 线性表在物理上存储时，通常以数组和链式结构的形式存储。

案例：蔬菜分为绿叶类、?类、菌菇类。线性表指的是具有部分相同特性的?类数据结构的集合

2.2顺序表分类

1.静态顺序表:

概念：使用定长数组存储元素

代码示例：

typrdef int SLDataType;
#define N 8
typedef struct SeqList
{
    SLDataType a[N];//定长数组
    int size;       //有效数据个数
}SL;

这就是一个静态顺序表，它又一定的缺陷。

2.动态顺序表

它的特点是：按需申请

3.动态顺序表的实现

我们首先创建相应的头文件和程序文件

我们现在头文件中，引用头文件，定义所需要的结构体和函数

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
typedef int SLDataType;

typedef struct SeqList
{
	SLDataType* arr; //存储数据的底层结构
	int capacity;    //记录顺序表的空间大小
	int size;        //记录顺序表当前有效的数据个数
}SL;
//初始化：
void SLInit(SL* ps);
//销毁
void SLDestroy(SL* ps);
//顺序表的头部 / 尾部插入
void SLPushFront(SL* ps, SLDataType x);
void SLPushBack(SL* ps, SLDataType x);
//顺序表的头部 / 尾部删除 
void SLPopBack(SL* ps);
void SLPopFront(SL* ps);

//打印
void SLPrint(SL* ps);
//删除指定位置的值
void SLInsert(SL* ps, int pos, SLDataType x);
void SLErase(SL* ps, int pos);

我们先定义一个动态顺序表

注意：这行代码是为了设定我们的数据类型

1.初始化

接下来我们要初始化我们的顺序表。所以我们定义了这个函数

接着我们去源文件写完这个函数，让指针指向NULL大小设定为0完成初始化

void SLInit(SL* ps) 
{
	ps->arr = NULL;
	ps->size = ps->capacity = 0;
}

写完了初始化我们可以开始写功能

首先就是头插和尾插

我们接着完善

2.头插

我们先来写头插函数

void SLPushFront(SL* ps, SLDataType x)

首先我们来思考以下问题，一个数组如何头插，以及目前的内存大小能否插入新的数据

假设足够：

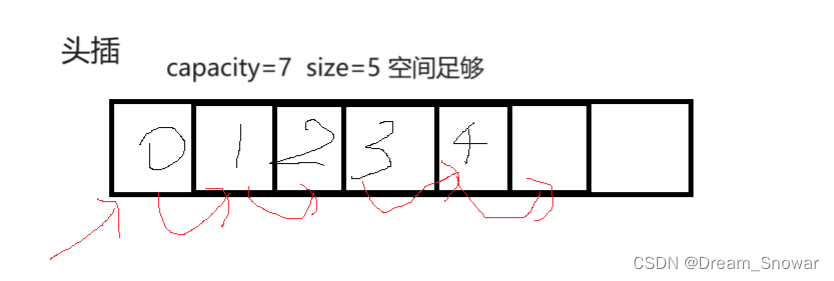
数组头插，我们一般将数组的各个元素后移一位然后将数组arr[0]赋值成我们要插入的数据

void SLPushFront(SL* ps, SLDataType x)
{
	assert(ps);
for (int i = ps->size; i > 0; i--) //i = 1
	{
		ps->arr[i] = ps->arr[i - 1]; //ps->arr[1] = ps->arr[0]
	}
	ps->arr[0] = x;
	ps->size++;
}

我们不难写出这个函数但是它对吗？

显然存在一定的问题，我们前面的条件是设置在空间充足的情况下，如果空间不足的话，我们该怎么办呢？

当然是扩容啦！！！

所以我们再写一个检查空间是否充足的函数，如果不足顺便扩容。

那么，既然说到扩容，我们应该怎样扩容呢？

我这里有三种扩容方式：

1.一次扩容一个空间

2.一次扩容多个大小的空间

3.成倍的增加空间（1.5倍，2倍）

这里我推荐第三种方法。

理由：

? ? ? ? 第一种一次扩容一个空间，好处是不会造成空间的浪费，缺点是如果我们输入大量数据时，它需要多次开辟，导致程序效率低下。

? ? ? ? 第二种一次开辟多个空间，有效解决了第一种导致程序小路低下的问题，但是，它也有相应的问题，我们不能确定一次开辟多大的空间合适，如果开辟小了，一样也会和第一种一样多次扩容，影响程序效率，但如果一下周四开辟空间过大，也会导致空间被浪费。

我们先定义函数：

void SLCheckCapacity(SL* ps)

接着判断是否需要扩容，然后扩容空间，但是由于我们初始化直接是NULL所以这里我再加上一个三目操作符，总体代码如下：

void SLCheckCapacity(SL* ps)
{
	if (ps->size == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		SLDataType* tmp = (SLDataType*)realloc(ps->arr, newCapacity * sizeof(SLDataType));
		if (tmp == NULL) {
			perror("realloc fail!");
			exit(1);
		}
		//扩容成功
		ps->arr = tmp;
		ps->capacity = newCapacity;
	}
}

这里我设置了tmp变量是为了防止扩容失败。这里我选择的就是扩容原来的两倍。

接下来我们按照上面的思路把头插完善

void SLPushFront(SL* ps, SLDataType x)
{
	assert(ps);
	SLCheckCapacity(ps);
	for (int i = ps->size; i > 0; i--) //i = 1
	{
		ps->arr[i] = ps->arr[i - 1]; //ps->arr[1] = ps->arr[0]
	}
	ps->arr[0] = x;
	ps->size++;
}

3.尾插

做完了头插，我们可以来试试尾插，数组中尾插是神简单的，如图：

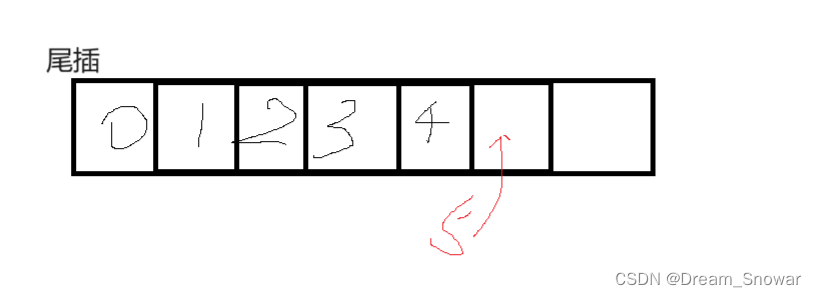
如果空间充足，我们可以直接再尾部插入我们的数据然后吧size++，不够的话先扩容然后再执行

void SLPushBack(SL * ps, SLDataType x)
{
		assert(ps);
		SLCheckCapacity(ps);
		ps->arr[ps->size++] = x;
}

这样头插和尾插就完成了

4.头删

完成了插入那么我们还需要完成删除，删除相比较插入它有什么不同？删除不需要太在意空间。

现在我们先来完成头删。

在数组中我们怎么完成头删的呢？如图

我们一般是把每个数向前移动一位，数组有效长度-1，及size--;

代码示例：

void SLPopFront(SL* ps)
{
	assert(ps);
	assert(ps->size);
	for (int i = 0; i < ps->size - 1; i++)
	{
		ps->arr[i] = ps->arr[i + 1];
	}
	ps->size--;
}

注意：我们要确保ps和ps->size不为NULL

5.尾删

这个操作实现起来其实非常简单，我们可以直接size--;

代码示例：

void SLPopBack(SL* ps)
{
	
	assert(ps);
	assert(ps->size);   
	ps->size--;
	
}

完成这些，那么我要上难度了，删除指定位置的值/插入指定位置的值

6.删除指定位置的值

具体思路，就是遍历去寻找所需数值，然后并将该数值之后的数据的下标前移，siza--如图：

代码示例：

void SLErase(SL* ps, int pos) {
	assert(ps);
	assert(pos >= 0 && pos < ps->size);

	//pos以后的数据往前挪动一位
	for (int i = pos; i < ps->size - 1; i++)
	{
		ps->arr[i] = ps->arr[i + 1];//ps->arr[i-2] = ps->arr[i-1];
	}
	ps->size--;
}

7.在指定位置插入值

思路，找到数值将该数值及其后的向后移动一位。size++

如图：

代码示例：

void SLInsert(SL* ps, int pos, SLDataType x) {
	assert(ps);
	assert(pos >= 0 && pos <= ps->size);

	SLCheckCapacity(ps);

	//pos及之后的数据往后挪动一位，pos空出来
	for (int i = ps->size; i > pos; i--)
	{
		ps->arr[i] = ps->arr[i - 1]; //ps->arr[pos+1] = ps->arr[pos]
	}
	ps->arr[pos] = x;
	ps->size++;
}

注：这是插入，要检查空间是否足够

8.打印

完成这些我们可以来尝试打印我们的顺序表，类似打印数组。

代码示例：

void SLPrint(SL* ps) 
{
	for (int i = 0; i < ps->size; i++)
	{
		printf("%d ", ps->arr[i]);
	}
	printf("\n");
} 

9.销毁顺序表

在我们之前讲过动态内存开辟，最后要再释放。

代码示例：

void SLDestroy(SL* ps) 
{
	assert(ps);

	if (ps->arr) {
		free(ps->arr);
	}
	ps->arr = NULL;
	ps->size = ps->capacity = 0;
}

最后来展示程序代码：

#include"SeqList.h"
void SLInit(SL* ps) 
{
	ps->arr = NULL;
	ps->size = ps->capacity = 0;
}
void SLDestroy(SL* ps)
{
	assert(ps);

	if (ps->arr) {
		free(ps->arr);
	}
	ps->arr = NULL;
	ps->size = ps->capacity = 0;
}
void SLCheckCapacity(SL* ps)
{
	if (ps->size == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		SLDataType* tmp = (SLDataType*)realloc(ps->arr, newCapacity * sizeof(SLDataType));
		if (tmp == NULL) {
			perror("realloc fail!");
			exit(1);
		}
		//扩容成功
		ps->arr = tmp;
		ps->capacity = newCapacity;
	}
}
void SLPushBack(SL * ps, SLDataType x)
{
		assert(ps);
		SLCheckCapacity(ps);
		ps->arr[ps->size++] = x;
}
void SLPushFront(SL* ps, SLDataType x)
{
	assert(ps);
	SLCheckCapacity(ps);
	for (int i = ps->size; i > 0; i--) //i = 1
	{
		ps->arr[i] = ps->arr[i - 1]; //ps->arr[1] = ps->arr[0]
	}
	ps->arr[0] = x;
	ps->size++;
}
void SLPopBack(SL* ps)
{
	
	assert(ps);
	assert(ps->size);   
	ps->size--;
	
}
void SLPopFront(SL* ps)
{
	assert(ps);
	assert(ps->size);
	for (int i = 0; i < ps->size - 1; i++)
	{
		ps->arr[i] = ps->arr[i + 1];
	}
	ps->size--;
}
void SLInsert(SL* ps, int pos, SLDataType x) {
	assert(ps);
	assert(pos >= 0 && pos <= ps->size);
	SLCheckCapacity(ps);
	for (int i = ps->size; i > pos; i--)
	{
		ps->arr[i] = ps->arr[i - 1]; //ps->arr[pos+1] = ps->arr[pos]
	}
	ps->arr[pos] = x;
	ps->size++;
}
void SLErase(SL* ps, int pos) 
{
	assert(ps);
	assert(pos >= 0 && pos < ps->size);
	for (int i = pos; i < ps->size - 1; i++)
	{
		ps->arr[i] = ps->arr[i + 1];
	}
	ps->size--;
}
void SLPrint(SL* ps) 
{
	for (int i = 0; i < ps->size; i++)
	{
		printf("%d ", ps->arr[i]);
	}
	printf("\n");
} 
void SLDestroy(SL* ps) 
{
	assert(ps);

	if (ps->arr) {
		free(ps->arr);
	}
	ps->arr = NULL;
	ps->size = ps->capacity = 0;
}
//指定位置之前插入数据
void SLInsert(SL* ps, int pos, SLDataType x) {
	assert(ps);
	assert(pos >= 0 && pos <= ps->size);

	SLCheckCapacity(ps);

	//pos及之后的数据往后挪动一位，pos空出来
	for (int i = ps->size; i > pos; i--)
	{
		ps->arr[i] = ps->arr[i - 1]; //ps->arr[pos+1] = ps->arr[pos]
	}
	ps->arr[pos] = x;
	ps->size++;
}
//删除指定位置数据
void SLErase(SL* ps, int pos) {
	assert(ps);
	assert(pos >= 0 && pos < ps->size);

	//pos以后的数据往前挪动一位
	for (int i = pos; i < ps->size - 1; i++)
	{
		ps->arr[i] = ps->arr[i + 1];//ps->arr[i-2] = ps->arr[i-1];
	}
	ps->size--;
}

这样一个循序表完成了，你可以用设计的函数来进行操作。