常见位运算模板方法总结（包含五道例题）

哈喽大家好，今天博主给大家带来算法基础常见位运算的模板，可以说大家遇到的百分之九十与位运算有关的题都可以用得上。话不多上我们上干货：

一.基础位运算符

<<? ?左移运算符

>>? ?右移运算符

~? ? ? 取反

&? ? ?与运算

|? ? ? ?或运算

^? ? ? ?或非

?对于前三个，我们都很熟悉，我们重点说一下后三位，既然我们标题说有模板，那么大家只要记住博主给大家总结口诀就可以了：

非常通俗易懂吧

&? ：? ? 0&0=1? ? ?1&0=0；????????有0就是0

|? ? ? ? ? ?1 | 1=1? ? ?1 | 0=1；? ? ? ? 有1就是1

^? ? ? ? ? 1^1=0? ? ?1^0=1? ? ? ? ? ? 相同为0，相异为1

二.给定一个数n，确定它的二进制表示中的第x位是0还是1

n=0 1 1 0 1 0 1 0 0 1

首先第一个知识点是二进制最低位是右边，所以我们在计算的时候是从右边从零计数

比如我们选择第六位，想判断它是不是1，只要&1不就行了，如果结果是1，说明第六位是1，反之则0，怎么找到第六位，只要向右移动6位不就就行了么

模板：

????????

（n>>x）&1

x是我们要查找的位数

如果大家没搞懂原理，直接用模板就可以，固定用法

三.将一个数n的二进制表示的第x位修改成1

n=0 1 1 0 1 0 1 0 1

仅将第x位修改成1，首先我们得用<<操作符把第x位移动到最低位，一直或运算是有1就为1，那么我们直接或等1不就行了

模板：

n|=(1<<x)

四.将一个数n的二进制表示的第x位修改成0

n=0 1 1 0 1 0 1 1 0 0

只要与上一条反着思考就行了

模板：

n&=(~(1<<x)）

五.提取一个数n二进制表示中最右侧的1

n = 0 1 1 1 0 1 0 1 0 0 0

根据n的二进制，最右侧的1在第四位，我们最后就是要把这个数变成这样：

模板：

n & -n

六.提取一个数n二进制表示中最右侧的1

n = 0 1 1 0 1 0 0 1?0

提取后，n就会变成这样：

?

模板：

n&(n-1)

第五个模板和第六个模板对应的例题

由于五，六模板有一些抽象，下边博主给大家带来三道题，都是用这两个模板解决的题目，让大家更深刻的理解模板的用法以及应用场景：

leetcode191 位1的个数：

191. 位1的个数 - 力扣（LeetCode）

观察这个运算：n?&?(n?1)? ?其运算结果恰为把 n?的二进制位中的最低位的 1?变为 0?之后的结果。

?题解：

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int ret = 0;
        while (n) {
            n &= n - 1;
            ret++;
        }
        return ret;
    }
};

leetcod368 比特位计数

338. 比特位计数 - 力扣（LeetCode）

题解：

class Solution {
    public int[] countBits(int n) {
        int[] bits = new int[n + 1];
        int highBit = 0;
        for (int i = 1; i <= n; i++) {
            if ((i & (i - 1)) == 0) {
                highBit = i;
            }
            bits[i] = bits[i - highBit] + 1;
        }
        return bits;
    }
}

leetcode461汉明距离

461. 汉明距离 - 力扣（LeetCode）

class Solution {
public:
    int countOnes(int x) {
        int ones = 0;
        while (x > 0) {
            x &= (x - 1);
            ones++;
        }
        return ones;
    }

    vector<int> countBits(int n) {
        vector<int> bits(n + 1);
        for (int i = 0; i <= n; i++) {
            bits[i] = countOnes(i);
        }
        return bits;
    }
};

?八.异或运算符运算的运算律

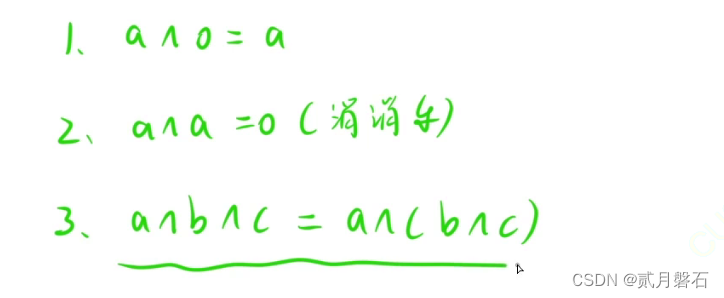
给大家带来两道例题：

136. 只出现一次的数字 - 力扣（LeetCode）

题解：

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ret=0;
        for(auto i :nums) ret^=i;
        return ret;
    }
};

260. 只出现一次的数字 III - 力扣（LeetCode）

题解：

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
        long long xs = 0;
        for (int& x : nums) {
            xs ^= x;
        }
        int lb = xs & -xs;
        int a = 0;
        for (int& x : nums) {
            if (x & lb) {
                a ^= x;
            }
        }
        int b = xs ^ a;
        return {a, b};
    }
};

?

好的，常见的所有位运算的模板都给大家列在这篇博客了，希望有帮助大家不要吝啬自己手里的关注呀。