【BI&AI】lecture 3 - GD & BP & CNN & Hands-on
GD & BP & CNN & Hands-on
专业术语
gradient descent (GD) 梯度下降
back propagation (BP) 向传播
Convolutional Neural Network (CNN) 卷积神经网络
forward propagation 前向传播
biologically symmetry 生物对称性
synaptic 突触
axon 轴突
课程大纲

The goal of AI: minimize the loss function
AI的任务目标就是解决优化函数,找到使得损失函数最小的参数
θ
\theta
θ:
Q: 什么是GD?
A: 梯度下降是一种优化算法,用于最小化或最大化目标函数。在神经网络中,我们通常希望最小化损失函数,以便使网络的预测结果与实际结果更接近。梯度下降通过迭代地更新网络参数来逐步调整模型,使损失函数逐渐减小。
使用线性回归举例说明如何实现这个目标
如下图,线性回归模型y=
β
\beta
βx,参数是
β
\beta
β,损失函数L(
β
\beta
β)。
可以直接求出二次函数的最小值,如下图中(b)所示,也可以使用GD求出最小值。
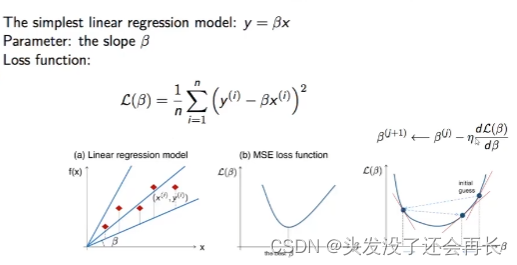
当参数很多的时候,依旧可以使用GD,比如有两个参数,最开始初始化
θ
\theta
θ为
θ
0
{\theta}^0
θ0,第一次GD:先对
θ
0
{\theta}^0
θ0求偏导,即对
θ
0
{\theta}^0
θ0中的两个参数分别求偏导,然后乘上学习率
η
\eta
η,得到的值用
▽
L
(
θ
)
{\bigtriangledown}L(\theta)
▽L(θ)表示,
θ
0
{\theta}^0
θ0-
▽
L
(
θ
)
{\bigtriangledown}L(\theta)
▽L(θ)便得到
θ
1
{\theta}^1
θ1 。一直不断地GD,直到L收敛,便找使得L最小的
θ
{\theta}
θ。

Gradient Descent to train Neural networks
在神经网络中,往往有上亿个参数,如果使用GD,每一次计算,都会有上亿个参数需要做GD,那如果要做到L收敛,GD的计算量是非常大的。所以,我们借助反向传播来解决问题。

Q: 直接使用梯度下降有什么问题?
A:
- 参数数量庞大:神经网络通常有大量的参数,特别是在深度神经网络中。如果直接计算每个参数对于损失函数的梯度,将需要非常大的计算开销和存储空间。
- 计算效率:在计算梯度时,需要通过前向传播计算网络的输出,然后通过反向传播计算每个参数对于损失函数的梯度。直接通过数值计算梯度需要执行大量的重复计算,效率较低。
BG
反向传播解决了这些问题,并提供了一种高效计算梯度的方法。通过使用链式法则,反向传播可以将梯度从输出层向输入层传播,利用相同的前向传播过程中计算的中间结果,避免了重复计算。这样可以大大减少计算开销,并使得神经网络的训练更加高效。
关于为什么反向传播可以利用前向传播的计算结果,大家可以参考这篇博客:深度学习——P13 Backpropagation,是李宏毅课程内容的笔记,大家也可去看李宏毅深度学习课程视频。
最后总结一下反向传播,如下图所示,在GD中是计算 L L L对 w w w的偏导(等同于上文的 θ \theta θ),在反向传播中转化为求 L L L对 z z z求偏导乘以 z z z对 w w w求偏导。 z z z对 w w w的偏导结果其实就是前项传播中计算的每一层输入,因为 z = w 1 x 1 + w 2 x 2 z=w_1x_1+w_2x_2 z=w1?x1?+w2?x2?,所以对 w w w求偏导,就得到 x 1 x_1 x1?和 x 2 x_2 x2?。这在前项传播中计算得到,不用再次计算。而 L L L对 z z z的偏导的计算也比较好算,因为 L L L的公式给出了,只需要根据公式计算就行,并且是一阶函数求导,这样大大简化了计算量。
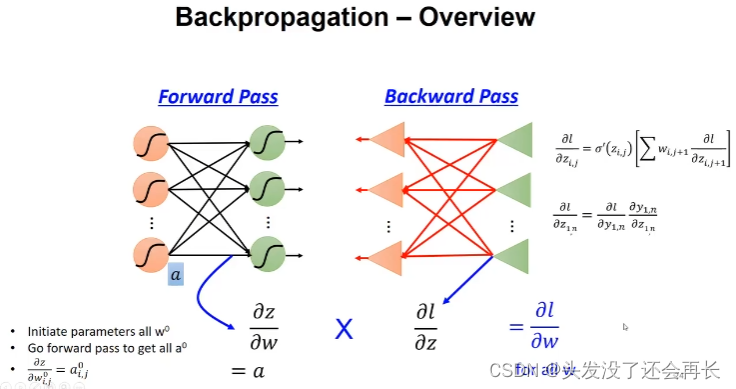
Backpropagation (BP) in the Brain?
大脑是使用反向传播算法去学习?现在没有直接的证据证明。
在大脑中实施BP有几个困难:

The Architecture of CNN
这部分大家可以直接看李宏毅老师的课程,也可以参考这篇博客——【李宏毅】深度学习-CNN(影像辨识为例)
Hands-on
自己手动建立CNN网络,使用CNN实现EEG降噪。输入:原始神经信号,输出:降噪后的神经信号。
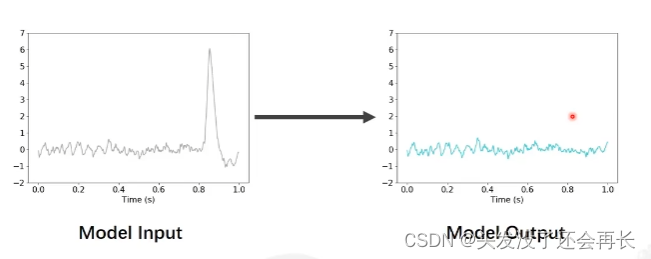
因为有时候采集的EEG信号存在噪声,我们可以使用神经网络来降噪,怎么做到呢?我们有许多的原始的EEG信号和这些信号降噪后的数据(label),将原始的EEG信号输入model,输出的结果和label计算loss,然后进行BP,这样我们的model就能够拟合出一个合适的参数,使得model的输出和label的差距最小,从而在训练结束后,我们可以使用这个model处理我们的数据进行降噪。
代码实现
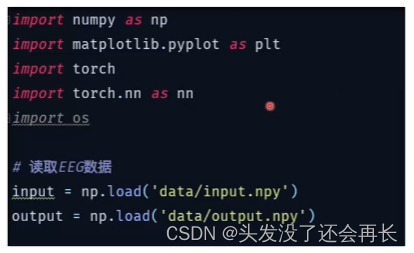
首先,调包并读取数据
然后构建CNN
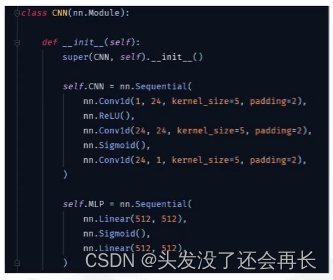 开始训练
开始训练

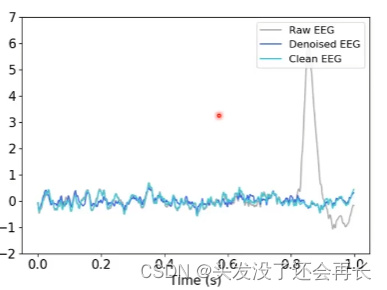
训练结果可视化

结果
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 如何在uni-app项目中进行数据持久化
- 《MyBatis-Plus 开发必备:自定义字符串格式化策略,保护用户隐私》
- Python武器库开发-武器库篇之密码生成器开发(四十九)
- 用React给XXL-JOB开发一个新皮肤(三):实现登录页和Layout骨架
- 2023年团体程序设计天梯赛——总决赛题
- 区块链技术在供应链管理中的革命性应用
- Python中__call__属性的使用指南详细解析
- sonar的详细介绍(1)
- 二次元个人主页引导页(林墨白优化版)
- VUE -- ESLint