决策规划框架 - （解耦：路径规划和速度规划 | 耦合：行为规划和轨迹规划）

1 解耦策略

1.1 概述

核心思想：
（1）路径规划：假定环境是“静态的”，将障碍物投影到参考路径上，并规划路径避开这些障碍物
（2）速度规划：根据路径规划给出的路径，将静态/动态障碍物投射到ST图上，并在ST图上规划一条速度曲线
Path planning

基于当前的静态环境，生成路径边界来描述可通行区域。通常，这是一个凸集，确保优化的质量
可以在Frenet $l(s)$和笛卡尔坐标系 $x(s),y(s)$下进行路径规划
Speed planning

投影：基于障碍物的预测信息，阻碍自车给定的路径的障碍物在图中用红色和橙色标记

$s(t)$的高阶导数信息也包含在ST图中，例如都是平行四边形，可以看出障碍物都是匀速运动

自动驾驶汽车轨迹优化的实时运动规划

Baidu Apollo EM Motion Planner

1.2 路径规划

1.2.1 SL 投影

SL Projection：将动态、静态障碍物投影到参考线，
（1）用上一帧规划周期的ST估计自车未来行为和低速动态障碍物是否会交互，通过路径优化器
（2）基于上面的投影过程，假设用于路径规划的“静态”环境

1.2.2 DP路径决策

（1）在自车前面采样多行点。点行之间的间隔取决于速度、道路结构
（2）不同行的点之间用五次多项式平滑地连接
（3）基于上述过程构造Lattice图，可以使用DP在图中找到最优路径
（4）提供一个路径的粗解，这条路径具有可行隧道和障碍物级别的决策

计算每条边的Cost：DP 路径决策

1.2.3 QP路径优化

（1）DP路径是次优的，因为Lattice图不能完全覆盖全局最优解
（2）五次样条QP路径是动态规划路径步骤的细化，构造一个凸空间

QP路径优化Cost函数设计

（1）这一步g(s)指的是DP路径，提供了对障碍物的距离
（2）使用线性化约束近似考虑航向的影响

1.3 速度规划

1.3.1 ST投影

（1）将静态障碍物和动态障碍物轨迹投影到路径规划SL的路径上，构建ST图
（2）速度规划的任务就是在ST图上找到最优曲线

1.3.2 DP速度决策

（1）和路径优化器类似，在ST图上找到最佳速度曲线是一个非凸优化问题
（2）DP结果包括分段线性速度曲线，基于DP结果构造可行凸区域和障碍物速度决策

基于离散的ST网格，高阶 导数用有限差分法近似

成本函数设计为：

1.3.3 QP速度优化

（1）分段线性速度曲线不能满足动力学要求，几乎不可能是全局最优解，需要用样条QP步骤优化
（2）与路径优化类似，基于五次样条的二次规划用于生成更精细的轮廓

五次样条速度优化的目标函数设计：

线性约束：

1.4 总结

DP + QP：
（1）使用DP在网格中搜索能得到一个粗解
（2）DP结果用于生成凸集并且引导QP
（3）QP用于搜索在凸区域里面的全局最优解

EM planner的缺陷：
（1）动态规划非常耗时

1 DP需要遍历图中的所有节点去获得最优解
2 与基于 A* 的方法相比，一个好的启发式函数可以快速引导算法找到最优解

（2）EM planner速度规划是次优的

例如如果速度限制依赖于位置，则对应于相同时间戳的速度约束随着优化过程速度曲线不断变化，使得问题非凸

2 耦合策略

（1）行为决策
目标是找到不同的机动行为，并找到一个最优的

(1) 变道决策：左右变道
(2) 障碍物决策：向左绕/向右绕，超车或跟车

（2）轨迹规划
轨迹规划是在相应的时空中生成局部平滑和安全的轨迹

2.1 行为规划

2.1.1 基于规则的变道决策（有限状态机）

基于规则的变道决策

优点：易于实施，强大的可解释性
缺点：可维护性差，可拓展性差

2.1.2 基于轨迹的变道决策

核心思想：
（1）不做出明确的车道决策，而是基于不同的目标车道规划轨迹，并且最终根据轨迹的最高质量做出决策
（2）确保决策和规划结果是一致的，不会突然做决定
（3）从轨迹规划的结果可以得到更详细的信息，使得决策更加合理

2.1.3 障碍物决策

（1）根据给定的目标车道，为静态或者动态障碍物做出决策（1 向左/向右绕 2 超车还是跟车）
（2）决策结果包括语义标签和时空安全走廊，以及粗糙的轨迹（后期需要平滑）

（1）行为模块将最优行为决策$b^{?}$和粗解轨迹${\tau }^{?}$传递给轨迹规划阶段
（2）对采样轨迹打分，并选择成本最低的轨迹作为行为规划的结果
（3）行为和轨迹模块使用相同的学习成本权重集最小化相同的成本函数

轨迹采样器（两段四次多项式）

纵向轨迹$s(t)$
横向轨迹$d(s)$

统一成本函数

障碍物、行驶路径和车道边界、航行速度、让路、路线、Cost to go、速度限制，行驶距离，动力学要求

行为决策包括障碍侧分配和车道信息
$b^{?}$编码为左右车道边界、行驶路径和障碍物分配，确定障碍物在时间t时刻停留在汽车的前后左右

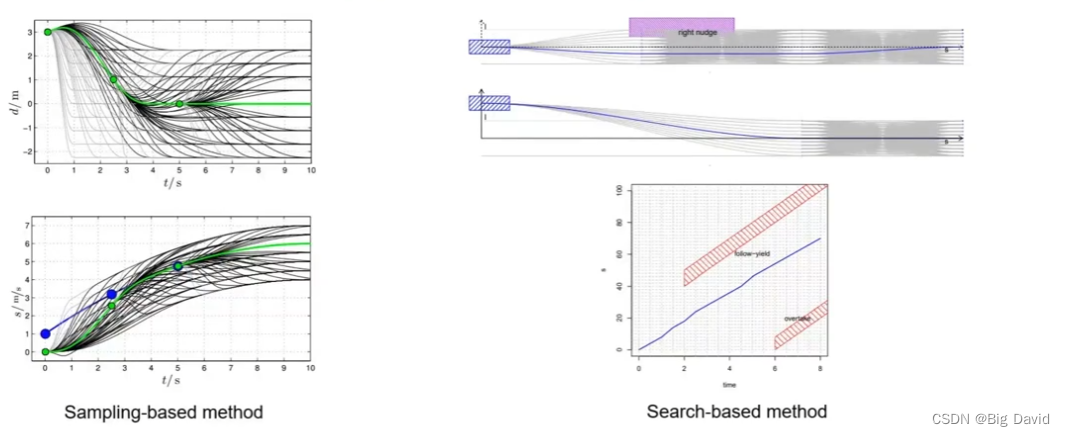
基于搜索/采样的障碍物决策

可以通过基于搜索（A*,DP,…)的规划算法和基于采样的方法规划粗解。

2.2 轨迹规划

基于时空联合的轨迹优化方法

输入：
（1）参考路径（目标车道）
（2）粗糙的轨迹
（3）时空安全走廊（障碍物决策）
输出：
轨迹：{$t\to (x,y,\theta ,v)$}
目标：
（1）安全：对于静态和动态障碍物无碰撞
（2）舒适：输出轨迹足够平滑
（3）动态可行：能够被控制器执行

目标函数设计：

约束设计：

把硬约束转换为软约束

对于约束函数：$g(x,u)＜0$，使用惩罚函数来惩罚违反约束的部分
对于不同类型的约束，选择具有不同惩罚程度的惩罚函数

简要介绍ILQR算法

目标函数和离散动力学

最优控制的解

定义cost-to-go函数

定义Q函数


使用行为决策的输出

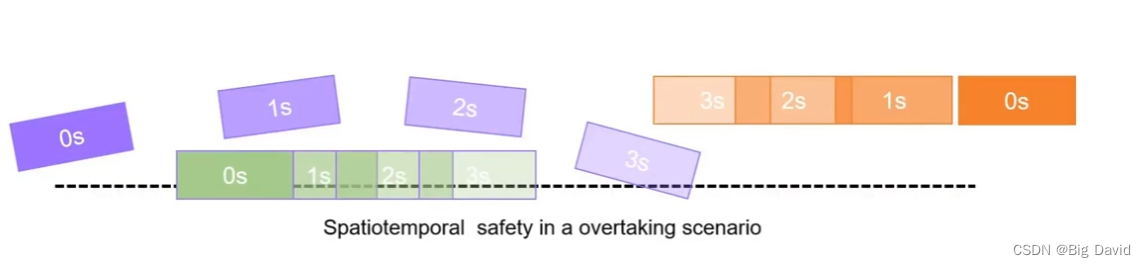
（1）约束从行为规划模块的输出生成的时空走廊轨迹
（2）凸可行区域使优化更加稳定