【数字图像处理】比特平面分割,对比空间平滑滤波器的尺寸对滤波效果,对比均值滤波器和中值滤波器对图像的平滑效果
实验目的
- 对比均值滤波器和中值滤波器对图像的平滑效果;
- 编程对比空间平滑滤波器的尺寸对滤波效果的影响;
- 编程对比均值滤波器和中值滤波器对图像的平滑效果。
实验方法
比特平面分割
比特平面分层,代替突出灰度级范围,突出特定比特来为整个图像外观作出贡献。像素是比特组成的数字,一幅8比特图像,能够认为是8个1比特的平面组成,其中平面1包含图像中全部像素的最低阶比特,而平面8包含图像中全部像素的最高阶比特,b表示比特(下标从0开始),B表示比特平面(下标从1开始)。
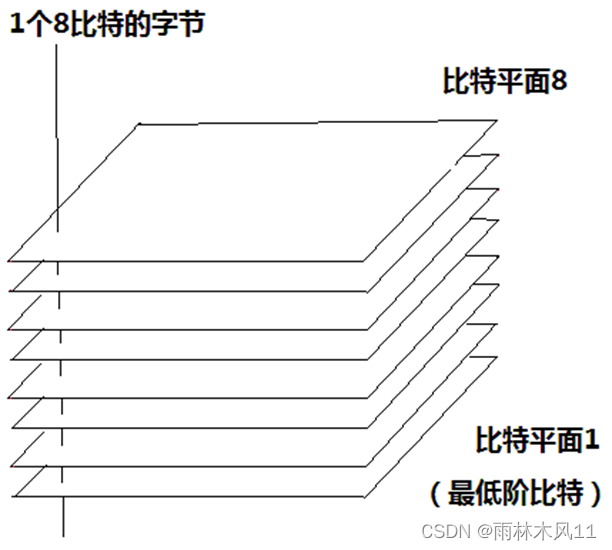
在8比特下,遍历整个图像,用像素值与各比特面的值2n-1(n为比特面)进行位与操做,判断该像素值在该比特面是否存在即该比特位是否为1,若是存在进行二值化给该像素值所在位赋值为255,这也是突出显示该比特的核心,不然赋值0。
程序代码如下:
clear all
orimg = imread('sparBIT.png');
orimg = rgb2gray(orimg);
figure;
subplot(3,3,1);
imshow(orimg);
title('原始图像');
[row,col] = size(orimg);
n = 8;
temppic = orimg;
for k = 1:n
for i = 1:row
for j = 1:col
tempbit = bitand(orimg(i,j),2^(k-1));
if tempbit == 2^(k-1)
temppic(i,j) = 255;
else
temppic(i,j) = 0;
end
end
end
subplot(3,3,k+1);
imshow(temppic);
title(['第',num2str(k),'比特图像 ']);
end
空间平滑滤波器
平滑滤波是低频增强的空间域滤波技术。它的目的有两类:一类是模糊;另一类是消除噪音。空间域的平滑滤波一般采用简单平均法进行,就是求邻近像元点的平均亮度值。邻域的大小与平滑的效果直接相关,邻域越大平滑的效果越好,但邻域过大,平滑会使边缘信息损失的越大,从而使输出的图像变得模糊,因此需合理选择邻域的大小。
本次我们使用的是简单均值滤波,表达式为
R
=
1
N
∑
i
=
1
N
z
i
R=\frac{1}{N} \sum_{i=1}^N z_i
R=N1?i=1∑N?zi?
以 为例,则是相当于一个 大小的模板在整个图像上滑动,在模板内求出像素平均值。此时表达式为
R
=
1
9
∑
i
=
1
9
z
i
R=\frac{1}{9} \sum_{i=1}^9 z_i
R=91?i=1∑9?zi?

我们采用尺寸大小分别 、 、 、 、 的平滑滤波器。程序代码如下:
clear all
orimg = imread('sparBIT.png');
orimg = rgb2gray(orimg);
figure;
subplot(2,3,1);
imshow(orimg);
title('原始图像');
[row,col] = size(orimg);
n = [3,5,9,15,35];
temppic = orimg;
for k = 1:5
fsize = n(k);
flt = ones(fsize,fsize);
for i = ceil(fsize/2):row-ceil(fsize/2)
for j = ceil(fsize/2):col-ceil(fsize/2)
temp = orimg(i-floor(fsize/2):i+floor(fsize/2),j-floor(fsize/2):j+floor(fsize/2));
temppic(i,j) = sum(temp(:))/(fsize*fsize);
end
end
subplot(2,3,k+1);
imshow(temppic);
title(['滤波器尺寸为',num2str(n(k)),'乘',num2str(n(k))]);
end
均值滤波器和中值滤波器对比
均值滤波器在前文已有描述。
一种非线性空间滤波器,其响应是基于图像滤波器所包围区域中像素(灰度)的排序,用排序结果的值代替中心像素的值。常见的如中值滤波器,该滤波器对脉冲噪声特有效。本节会进行均值滤波器和中值滤波器滤波效果的对比。
代码如下:
clear all
orimg = imread('sparBIT.png');
orimg = rgb2gray(orimg);
figure;
subplot(3,2,1);
imshow(orimg);
title('原始图像');
subplot(3,2,2);
imshow(orimg);
title('原始图像');
[row,col] = size(orimg);
n = [3,5,9,15];
temppic_ave = orimg;
temppic_mid = orimg;
for k = 1:2
fsize = n(k);
flt = ones(fsize,fsize);
for i = ceil(fsize/2):row-ceil(fsize/2)
for j = ceil(fsize/2):col-ceil(fsize/2)
temp = orimg(i-floor(fsize/2):i+floor(fsize/2),j-floor(fsize/2):j+floor(fsize/2));
temppic_ave(i,j) = sum(temp(:))/(fsize*fsize);
temppic_mid(i,j)= median(temp(:));
end
end
subplot(3,2,2*k+1);
imshow(temppic_ave);
title(['均值滤波',num2str(n(k)),'乘',num2str(n(k))]);
subplot(3,2,2*k+2);
imshow(temppic_mid);
title(['中值滤波',num2str(n(k)),'乘',num2str(n(k))]);
end
实验结果
比特平面分割

可以发现,较高位的比特图像含有更多的信息
如果要进行重构,则是使用第n个平面的像素值乘以常数 2^(n-1),可以发现,用128乘以比特平面8,用64乘以比特平面7,然后将这两个平面相加,原图的主要特征便被复原了。
空间平滑滤波器的尺寸对滤波效果的影响

可以发现,m=3和m=5结果区别不明显,噪声显著降低。随着尺寸的增大,会导致图像变得越来越模糊,细节难以区分。
均值滤波器和中值滤波器对比

可以通过对比发现,中值滤波器比均值滤波器有着更好的效果。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Python更换国内镜像源
- 2023江苏职教高考计算机技能考试--改错题解析
- 零日漏洞:威胁与应对
- U9 语义分析和代码生成
- SpringBoot - application.yml 多环境切换解决方案
- element input组件自动失去焦点问题解决
- 如何在ubuntu22.04安装ROS2
- 大数据学习(27)-Yarn总结与注意事项
- SCAU:1107 文本文件操作_单词的排序
- 代码随想录算法训练营第二十三天 | 修建二叉搜索树