一元二次方程虚数解

对一元二次方程ax2+bx+c=0 (a≠0)；若判别式△=b2-4ac<0,则方程无实根,虚数解为：x=(-b± i√(4ac-b2))/(2a)。
只含有一个未知数（一元），并且未知数项的最高次数是2（二次）的整式方程叫做一元二次方程[1] 。一元二次方程经过整理都可化成一般形式ax2+bx+c=0（a≠0）。其中ax2叫作二次项，a是二次项系数；bx叫作一次项，b是一次项系数；c叫作常数项。一元二次方程成立必须同时满足三个条件：①是整式方程，即等号两边都是整式，方程中如果有分母；且未知数在分母上，那么这个方程就是分式方程，不是一元二次方程，方程中如果有根号，且未知数在根号内，那么这个方程也不是一元二次方程（是无理方程）。②只含有一个未知数；③未知数项的最高次数是2。


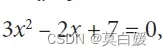
解:
Δ=(-2)^2-4×3×7=-80
√Δ=√-80=√80×√-1=(2√10)i
(i=√-1,称为虚数单位)
X=(-(-2)±√Δ)/2
=〔4±(2√10)i〕/2
=2±(√10)i
即:X1=2+(√10)i
X2=2-(√10)i