堆排序算法
发布时间:2023年12月21日
首先得知道堆是一种完全二叉树的数据结构,可以分为最大堆和最小堆,堆的储存方式是用一维数组储存。
如下图就是最小堆,而最大堆就是最小堆倒过来,上面的数要大于下面的数
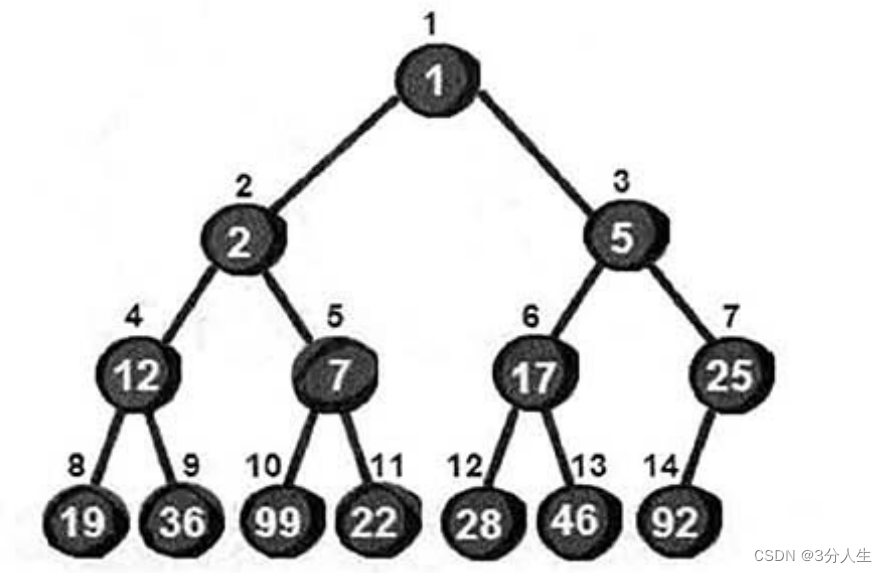
1.为什么堆可以实现排序?我们知道最小堆的最上面的数一定是最小的(最大堆最上面是最大的),因此堆排序的过程就是取出堆的根部最大或最小值,然后再去维护堆变成最大堆或最小堆,再取出,再维护的过程,而维护的过程时间复杂度是O(logN),取出所有数的时间复杂度是O(N),因此整体时间复杂度是O(NlogN)和快速排序一样的。
如下面代码就是堆排序,输入sum代表数组元素的个数,再输入sum个元素,然后进行从小到大排序后输出结果
#include<stdio.h>
int a[100], n;
void swap(int x, int y)//定义函数交换数组
{
int t;
t = a[x]; a[x] = a[y]; a[y] = t;
}
void siftdown(int x)//维护最大堆操作,即将a[x]这个元素和他的儿子进行比较交换
{
int t, flag = 0;
while (flag == 0 && 2 * x <= n)//不是最大堆且至少有左儿子
{
if (a[x] < a[2 * x])
t = 2 * x;
else
t = x;
if (a[t] < a[2 * x + 1] && 2 * x + 1 <= n)//存在右儿子
t = 2 * x + 1;
if (t != x)//存在儿子比本身大
{
swap(t, x);//进行交换
x = t;
}
else//不存在儿子比本身大,即满足了最大堆
flag = 1;
}
}
void creat()//建立最大堆
{
int i = n / 2;
while (i)
{
siftdown(i);
i--;
}
}
int main()
{
int sum, i;//sum表示需要排序的元素个数
scanf("%d", &sum);
n = sum;
for (i = 1; i <= sum; i++)//循环输入原来元素放进a数组里面
scanf("%d", &a[i]);
creat();//建立最大堆
while (n > 1)//遍历sum个元素
{
swap(1, n);//交换第一个元素即堆的根部和最后一个元素
n--;//此时数组最后一个元素是最大的了,所以不用考虑了进行n--
siftdown(1);//重新维护最大堆
}
for (i = 1; i <= sum; i++)//输出排序后的结果
{
printf("%d ", a[i]);
}
return 0;
}
文章来源:https://blog.csdn.net/2301_80336512/article/details/135135726
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 小狐狸ChatGPT系统 不同老版本升级至新版数据库结构同步教程
- 一款真正可用的支付系统,可搭建自己的易支付系统,开源无后门
- 「Verilog学习笔记」使用握手信号实现跨时钟域数据传输
- Springboot+vue整合 支付宝沙箱支付
- GPT-5不叫GPT-5?下一代模型会有哪些新功能?
- 非隔离恒压ACDC稳压智能电源模块芯片推荐:SM7015
- 关于OpenCV中 CV_Assert() 的使用引起程序中止/崩溃问题
- 如何用Rust编程访问未知结构的json串?
- 【linux 多线程并发】多线程的控制,挂起线程暂停运行,直到唤醒线程,取消线程运行,可以设置合适的取消点属性避免不安全点被中止
- RWKV入门