代码随想录算法训练营第四十天|343. 整数拆分、96.不同的二叉搜索树

题目：343. 整数拆分

文章链接：代码随想录

视频链接：LeetCode:343.整数拆分

题目链接：力扣题目链接

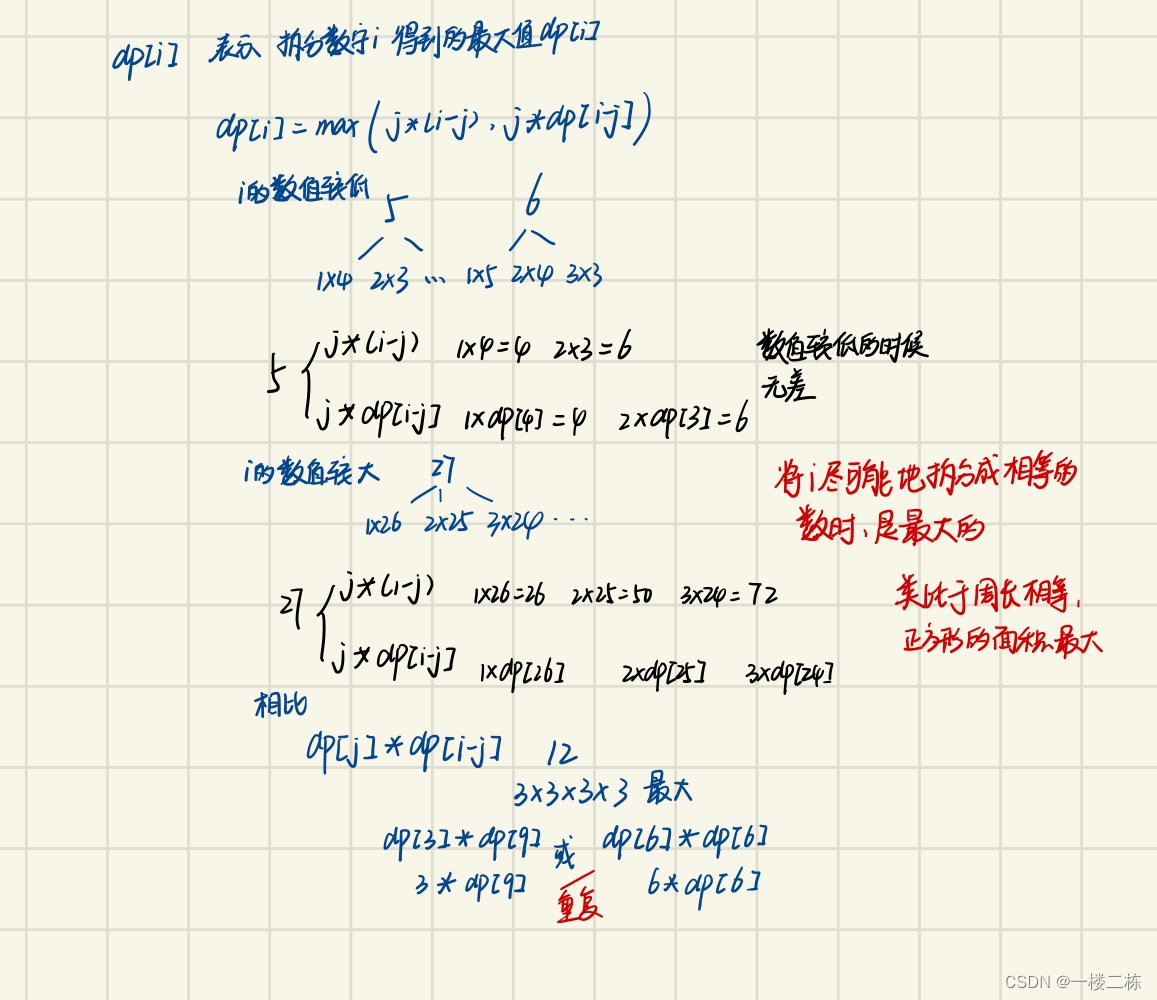
图释：

class Solution {
public:
    // 确定dp数组（dp table）以及下标的含义dp[i], 表示拆分数字i的最大乘积dp[i]  
    // 确定递推公式      dp[i] = max(dp[i], j*dp[i-1], j*(i-j))
    // dp数组如何初始化  因为题目要求必须拆分K个正整数，所以0和1是拆分不了的，dp[0]=dp[1]=0; dp[2]=1 
    // 确定遍历顺序      从小到大
    // 举例推导dp数组

    int integerBreak(int n) {
        vector<int> dp(n+1, 0);
        dp[0]=dp[1]=0;
        dp[2]=1;
        if(n==0 || n==1)return 0;
        if(n==2) return 1;
        for(int i=3; i<=n; i++){
            for(int j=1; j<=i/2; j++){
                dp[i] = max(dp[i], max(j*(i-j), j*dp[i-j])); //max只能比较两个数
            }
        }
        return dp[n];
    }
};

class Solution {
public:

    int integerBreak(int n) {
        if(n==0 || n==1)return 0;
        if(n==2) return 1;
        if(n==3) return 2;
        if(n==4) return 4;
        int result = 1;
        while(n>4){
           // 尽可能地拆成n个3
           result *=3;
           n -= 3;
        }
        // 
        result *= n; //到最后不够4时，再乘以剩余的数 
        return result;
    }
};

题目：96.不同的二叉搜索树

文章链接：代码随想录

视频链接：LeetCode:96.不同的二叉搜索树

题目链接：力扣题目链接

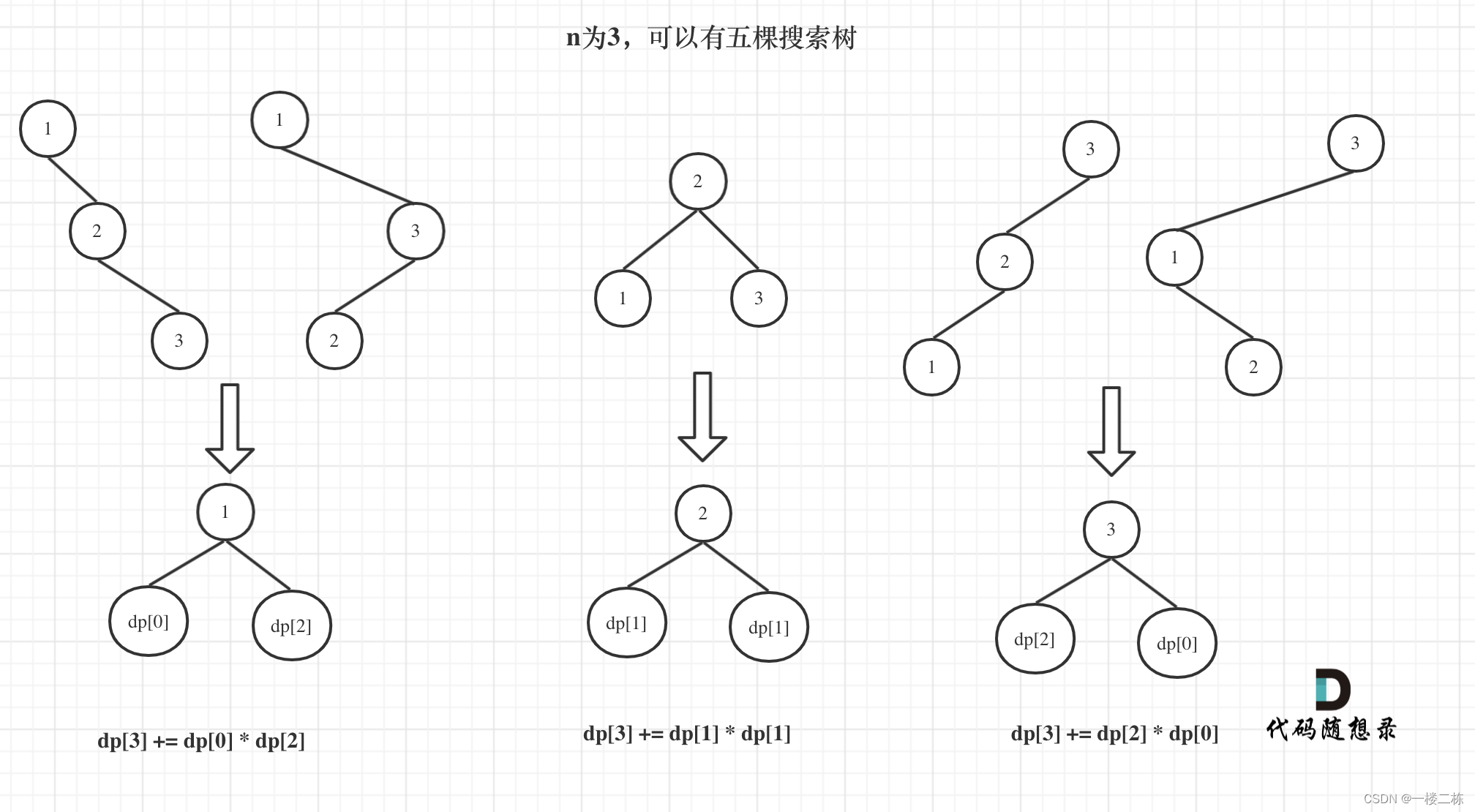
图释：

class Solution {
public:
    // 确定dp数组以及下标的含义dp[i], dp[i]表示整数i能构造dp[i]种不同的二叉搜索树  
    // 确定递推公式      dp[i] = dp[j] * dp[i-j]  
    // dp数组如何初始化  dp[0]表示叶子节点，也算一个二叉树 dp[0]=1
    // 确定遍历顺序      从上到下
    // 举例推导dp数组
    int numTrees(int n) {
        if(n==0) return 1;
        vector<int> dp(n+1, 0);
        dp[0] = 1;
        for(int i=1; i<=n; i++){
            // 计算从1到n的dp[n]值
            for(int j=1; j<=i; j++){  
                // 以j作为头节点
                dp[i] += dp[j-1] * dp[i-j];   // j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量
                //dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
            }
        }
        return dp[n];
    }
};