球形体积雾
前言
本Blog的体积雾散射算法借鉴自Miles Macklin Simulation and computer graphics,如需原文参照,可转至链接。
球形体积雾
球形体积雾,即通过一个球体,配备一个雾效Shader,从而模拟出球状雾效。
主要包括:
- 首先球体得是透明物体,而且需要在其他透明物体渲染之后进行。
- 传入数据包括:
- 体积雾颜色
- 体积雾中心坐标和半径
- 体积雾强度,最大雾效因子(好像没用到),雾效衰减
- 在vert中将摄像机之后的片元放置到摄像机近处,防止片元被clip后雾效错误。(借鉴ShadowMap的做法)
#if UNITY_REVERSED_Z
positionCS.z = min(positionCS.z, UNITY_NEAR_CLIP_VALUE);
#else
positionCS.z = max(positionCS.z, UNITY_NEAR_CLIP_VALUE);
#endif
- 向fragment传入顶点的屏幕坐标Position(
o.uv = ComputeScreenPos(o.vertex);)
ComputeScreenPos返回的值是齐次坐标系下的屏幕坐标值,其范围为[0, w]。
在Unity内置Shader中,获取阴影UV使用如下代码
float4 GetShadowCoord(VertexPositionInputs vertexInput)
{
#if defined(_MAIN_LIGHT_SHADOWS_SCREEN) && !defined(_SURFACE_TYPE_TRANSPARENT)
return ComputeScreenPos(vertexInput.positionCS);
#else
return TransformWorldToShadowCoord(vertexInput.positionWS);
#endif
}
- 在fragment中获取到该片元的深度,通过深度计算得到该点在WorldSpace下的pos
// 通过深度计算得到直接坐标
real depth = SAMPLE_DEPTH_TEXTURE(_CameraDepthTexture, sampler_CameraDepthTexture, i.texcoord);
float3 worldPos = ComputeWorldSpacePosition(i.texcoord, depth, UNITY_MATRIX_I_VP);
ComputeWorldSpacePosition定义在Common.hlsl
float3 ComputeWorldSpacePosition(float2 positionNDC, float deviceDepth, float4x4 invViewProjMatrix)
{
float4 positionCS = ComputeClipSpacePosition(positionNDC, deviceDepth);
float4 hpositionWS = mul(invViewProjMatrix, positionCS);
return hpositionWS.xyz / hpositionWS.w;
}
float3 ComputeWorldSpacePosition(float4 positionCS, float4x4 invViewProjMatrix)
{
float4 hpositionWS = mul(invViewProjMatrix, positionCS);
return hpositionWS.xyz / hpositionWS.w;
}
ComputeClipSpacePosition(float2 positionNDC, float deviceDepth)将NDC空间转移到Clip空间
float4 ComputeClipSpacePosition(float2 positionNDC, float deviceDepth)
{
float4 positionCS = float4(positionNDC * 2.0 - 1.0, deviceDepth, 1.0);
#if UNITY_UV_STARTS_AT_TOP
// Our world space, view space, screen space and NDC space are Y-up.
// Our clip space is flipped upside-down due to poor legacy Unity design.
// The flip is baked into the projection matrix, so we only have to flip
// manually when going from CS to NDC and back.
positionCS.y = -positionCS.y;
#endif
return positionCS;
}
// Use case examples:
// (position = positionCS) => (clipSpaceTransform = use default)
// (position = positionVS) => (clipSpaceTransform = UNITY_MATRIX_P)
// (position = positionWS) => (clipSpaceTransform = UNITY_MATRIX_VP)
float4 ComputeClipSpacePosition(float3 position, float4x4 clipSpaceTransform = k_identity4x4)
{
return mul(clipSpaceTransform, float4(position, 1.0));
}
- 当下,我们已经获取到了片元的深度点的世界空间坐标值,我们还通过CPU传入了球形雾效的世界空间中心点坐标和半径。
之后,我们计算球形体积雾雾效因子。
球形体积雾计算方法1
由此,我们可以计算远处片元反射的光线,要穿过多厚的雾,才能到达我们的眼睛。因为雾效是局部的而不是全局的,因此我们需要计算穿过的雾效厚度L:

根据上图有:
d
i
r
→
=
(
P
?
E
)
.
n
o
r
m
a
l
i
z
e
d
∣
E
X
∣
=
d
o
t
(
d
i
r
→
,
E
C
→
)
∣
C
X
∣
2
=
∣
E
C
∣
2
?
∣
E
X
∣
2
\overrightarrow{dir} = (P-E).normalized\\ |EX| = dot(\overrightarrow{dir}, \overrightarrow{EC})\\ |CX|^2 = |EC|^2 - |EX|^2
dir=(P?E).normalized∣EX∣=dot(dir,EC)∣CX∣2=∣EC∣2?∣EX∣2
射线与圆的相交的判定条件为:
∣
C
X
∣
2
<
R
2
(
直线穿过球内
)
|CX|^2<R^2(直线穿过球内)
∣CX∣2<R2(直线穿过球内)
当条件符合后,再进行雾效计算,有:
L
2
=
R
2
?
∣
C
X
∣
2
\frac{L}{2} = \sqrt{R^2-|CX|^2}
2L?=R2?∣CX∣2?
当摄像机在球形范围外,即
∣
E
X
∣
>
L
2
∣
∣
∣
E
X
∣
<
?
L
2
|EX|>\frac{L}{2} \quad||\quad |EX|<-\frac{L}{2}
∣EX∣>2L?∣∣∣EX∣<?2L?
- 当
∣
E
X
∣
>
L
2
|EX|>\frac{L}{2}
∣EX∣>2L? ,光线经过整个雾球,雾球内距离为L
L = 2 R 2 ? ∣ C X ∣ 2 L = 2\sqrt{R^2-|CX|^2} L=2R2?∣CX∣2? - 当 ∣ E X ∣ < ? L 2 |EX|<-\frac{L}{2} ∣EX∣<?2L? ,整个雾球在光线背后,雾球内距离为0
当相机在球形范围内,雾球内距离为 L/2 + |EX|
- 若 ∣ E X ∣ > 0 |EX|>0 ∣EX∣>0 ,光线经过大半个雾球,雾球内距离为 L/2 + |EX|
- 若 ∣ E X ∣ < 0 |EX|<0 ∣EX∣<0 ,光线经过小半个雾球,雾球内距离为 L/2 + |EX|(与上面相同,因为|EX|为负)
综上:有代码如下
/// <summary>
/// describe:
/// BallFogFactor的另一种算法
/// params:
/// depthPosWS: 深度图中记录深度点的世界坐标
/// fogBallCenterRadiusWS: 世界空间中球形体积雾的信息(位置+半径)
/// fogDensity: 雾效强度
/// fogMaxFactor: 最大雾效因子
/// falloffDist: 衰减系数 * 半径 * 0.5f
/// <summary>
half CalculateBallFogFactor2(
float3 depthPosWS, float4 fogBallCenterRadiusWS,
float fogDensity, float fogMaxFactor, float falloffDist
)
{
// 数据提取
float R = fogBallCenterRadiusWS.w;//R
float3 C = fogBallCenterRadiusWS.xyz;//C
float3 E = GetCameraPositionWS();//E
// 数据计算
float3 cameraToDepthPoint = depthPosWS - E;
float depthT = length(cameraToDepthPoint);// 深度距离
float3 dir = normalize(cameraToDepthPoint);// dir
float3 EC = center - camPosWS;
float EX = dot(dir,EC);
float CX_2 = dot(EC,EC) - EX * EX;
//判定
float R_2 = R * R;
if(CX_2 >= R_2) return 0;//直线不穿过球内,没有雾效
float LDiv2 = sqrt(R_2 - CX_2);//sqrt{L}{2}
float L = 2 * LDiv2;
if(EX < - LDiv2)return 0;//射线不穿过球内,没有雾效
// 判定通过,计算雾效距离
float FogDistance;
if(EX > LDiv2) FogDistance = L; //光线经过整个雾球
else FogDistance = LDiv2 + EX; //摄像机在雾效范围内
// 如果雾是均匀雾,我们就可以返回雾效因子为
float FogFactor = clamp(0, fogMaxFactor, FogDistance * fogDensity);
return FogFactor;
}
运行后发现,我们忘记处理了一种情况,当深度点在雾效球内,或雾效之前,我们需要删掉被遮挡的雾效。
增加代码:// 如果最大深度小于雾效深度,需要减去被遮挡的雾距离。
/// <summary>
/// describe:
/// BallFogFactor的另一种算法,该方法使用几何信息递推求解
/// 但这种方法暂时只支持均匀分布的雾效
/// 具体推导过程见Blog《光在雾效中的散射》
/// params:
/// depthPosWS: 深度图中记录深度点的世界坐标
/// fogBallCenterRadiusWS: 世界空间中球形体积雾的信息(位置+半径)
/// fogDensity: 雾效强度
/// fogMaxFactor: 最大雾效因子
/// falloffDist: 衰减系数 * 半径 * 0.5f
/// <summary>
half CalculateBallFogFactor2(
float3 depthPosWS, float4 fogBallCenterRadiusWS,
float fogDensity, float fogMaxFactor, float falloffDist
)
{
// 设:
// float R: 球的半径
// float3 C:球的中心世界坐标
// float3 E:摄像机的世界坐标
// float3 X:光线所在的直线上距离球心最近的点
// float3 dir:光线的方向(摄像机到像素点的方向)
// 设定:
// XX_2:表示XX的平方,如果XX为向量,则表示距离的平方。
// 数据提取
float R = fogBallCenterRadiusWS.w;
float3 C = fogBallCenterRadiusWS.xyz;
float3 E = GetCameraPositionWS();
// 数据计算
float3 cameraToDepthPoint = depthPosWS - E;
float depthT = length(cameraToDepthPoint);// 深度距离
float3 dir = normalize(cameraToDepthPoint);// dir
float3 EC = C - E;
float EX = dot(dir,EC);
float CX_2 = dot(EC,EC) - EX * EX;
//判定
float R_2 = R * R;
if(CX_2 >= R_2) return 1;//直线不穿过球内,没有雾效
float LDiv2 = sqrt(R_2 - CX_2);//sqrt{L}{2}
float L = 2 * LDiv2;
if(EX < - LDiv2)return 1;//射线不穿过球内,没有雾效
// 判定通过,计算雾效距离
float RayDistance = EX + LDiv2;//光线从摄像机发出,到穿过雾时移动的距离
float FogDistance = 1;
if(EX > LDiv2) FogDistance = L; //光线经过整个雾球
else FogDistance = LDiv2 + EX; //摄像机在雾效范围内
// 如果最大深度小于雾效深度,需要减去被遮挡的雾距离。
float DivDistance = 0;
if(depthT < RayDistance){
DivDistance = RayDistance - depthT;
}
FogDistance -= DivDistance;
if(FogDistance<0)FogDistance = 0;
// 如果雾是均匀雾,我们就可以返回雾效因子为
half FogFactor = clamp(0,1-fogMaxFactor,FogDistance * fogDensity);
return 1-FogFactor;
}
然而,再增加条件:如果雾效并不是均匀分布的,那我们如何处理。
首先我们知道进入点距离球心为R,退出点也距离球心为R。
如果衰减函数为
y
=
?
k
x
+
1
(
k
>
0
)
y = -kx + 1(k>0)
y=?kx+1(k>0);
球心边缘y为0,球心中心y为1,则进入点雾效距离x = R,中心点雾效距离为x = CX。
中间任意一点雾效距离为:
x
=
t
2
+
C
X
2
x = \sqrt{t^2 + CX^2}
x=t2+CX2?
故整体雾效强度为
2
∫
t
=
0
t
=
L
2
?
k
t
2
+
C
X
2
+
1
(
d
t
)
2\int_{t=0}^{t=\frac{L}{2}} -k \sqrt{t^2 + CX^2} + 1 (dt)
2∫t=0t=2L???kt2+CX2?+1(dt)
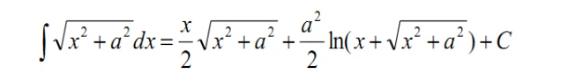
但是这样求解的是全部雾效的强度,但是片元有可能在雾效内,雾效前。所以不能全部积分。
根据t的取值,对积分区间求解,最终得到最后的结果。
那既然我们需要一个参数t得知光线在其中的位置,何不直接在计算时,得到光线在雾内传播的起始t值,和结束t值。
球形体积雾计算方法2
// 设:
// float r: 球的半径
// float3 C:球的中心世界坐标
// float3 E:摄像机的世界坐标
// float3 X:光线所在的直线上的点
// float3 dir:光线的方向(摄像机到像素点的方向)
设:光线函数为
X
(
t
)
=
E
+
D
i
r
?
t
(
D
i
r
为单位向量
)
X(t) = E + Dir * t(Dir为单位向量)
X(t)=E+Dir?t(Dir为单位向量)
当光线和球面相交,公式为:
∣
X
(
t
)
?
C
∣
2
=
r
2
|X(t) - C|^2 = r^2
∣X(t)?C∣2=r2
代入公式,得:
∣
E
+
D
i
r
?
t
?
C
∣
2
=
r
2
|E + Dir * t - C|^2 = r^2
∣E+Dir?t?C∣2=r2
注意:因为这里 r 为float,而 E、Dir、C 为向量,故不能将 r 放入平方内。
我们展开公式,并整理得:
∣
D
i
r
∣
2
t
2
+
2
(
∣
E
?
C
∣
?
D
i
r
)
?
t
+
(
∣
E
?
C
∣
2
?
r
2
)
=
0
|Dir|^2t^2 + 2(|E-C| \cdot Dir) * t + (|E-C|^2-r^2) = 0
∣Dir∣2t2+2(∣E?C∣?Dir)?t+(∣E?C∣2?r2)=0
求解2次方程:公式我居然忘了!!!!
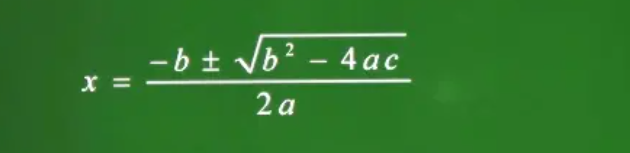
得到
t
m
i
n
t_{min}
tmin?,
t
m
a
x
t_{max}
tmax?
继续计算得到场景中实际的t值。
0
<
=
t
m
i
n
<
=
d
e
p
t
h
T
0<=t_{min}<=depthT
0<=tmin?<=depthT
t m i n < = t m a x < = d e p t h T t_{min}<=t_{max}<=depthT tmin?<=tmax?<=depthT
最后得到传播距离为
f
o
g
D
i
s
t
=
t
m
a
x
?
t
m
i
n
;
fogDist = t_{max} - t_{min};
fogDist=tmax??tmin?;
同样我们需要考虑雾效衰减的问题。
雾效衰减该部分内容属于公司文件,这里就不再阐述。(怕收到律师函)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 聚道云软件连接器助力某半导体行业公司实现访客管理自动化
- 与AI合作 -- 写一个modern c++单例工厂
- 【Go语言入门:Go程序的流程控制语句】
- Adobe Premier及PrElements各版本安装指南
- GBASE南大通用-管理用户定义函数(UDF)
- 【Leetcode】83. 删除排序链表中的重复元素
- Python实现递归最小二乘法回归模型(RecursiveLS算法)项目实战
- 弱势行情下,股票如何赚钱?具体操作方法!——(内容丰富面广,建议收藏)
- (菜鸟自学)渗透测试导论
- linux ftp服务选择与ftp(vsftpd,Pure-FTPd)服务安装使用教程