Java二分查找冒泡排序插入排序
发布时间:2024年01月07日
二分查找
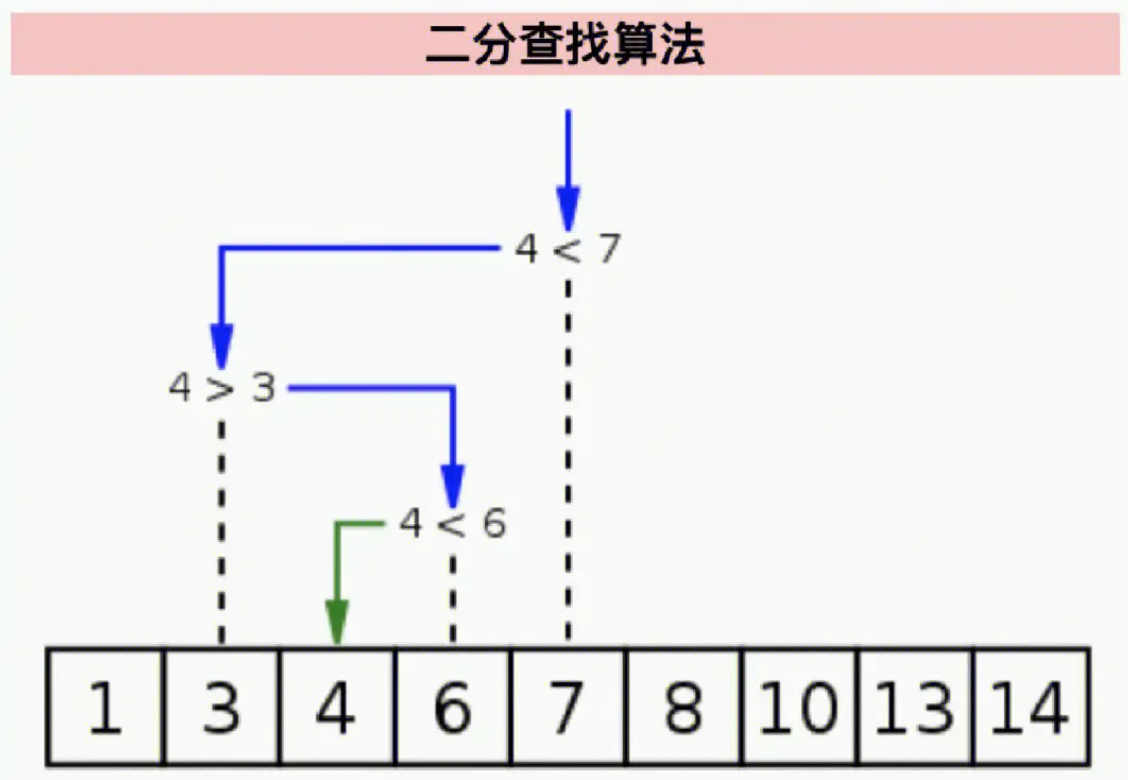
又叫折半查找,要求待查找的序列有序。每次取中间位置的值与待查关键字比较,如果中间位置的值比待查关键字大,则在前半部分循环这个查找的过程,如果中间位置的值比待查关键字小,则在后半部分循环这个查找的过程。直到查找到了为止,否则序列中没有待查的关键字。
public static int biSearch(int[] array, int a) {
int lo = 0;
int hi = array.length - 1;
int mid;
while (lo <= hi) {
mid = (lo + hi) / 2;//中间位置
if (array[mid] == a) {
return mid + 1;
} else if (array[mid] < a) { //向右查找
lo = mid + 1;
} else { //向左查找
hi = mid - 1;
}
}
return -1;
}
冒泡排序算法

(1)比较前后相邻的二个数据,如果前面数据大于后面的数据,就将这二个数据交换。
(2)这样对数组的第 0 个数据到 N-1 个数据进行一次遍历后,最大的一个数据就“沉”到数组第N-1 个位置。
(3)N=N-1,如果 N 不为 0 就重复前面二步,否则排序完成。
public static void bubbleSort1(int[] a, int n) {
int i, j;
for (i = 0; i < n; i++) {//表示 n 次排序过程。
for (j = 1; j < n - i; j++) {
if (a[j - 1] > a[j]) {//前面的数字大于后面的数字就交换
//交换 a[j-1]和 a[j]
int temp;
temp = a[j - 1];
a[j - 1] = a[j];
a[j] = temp;
}
}
}
}
插入排序算法
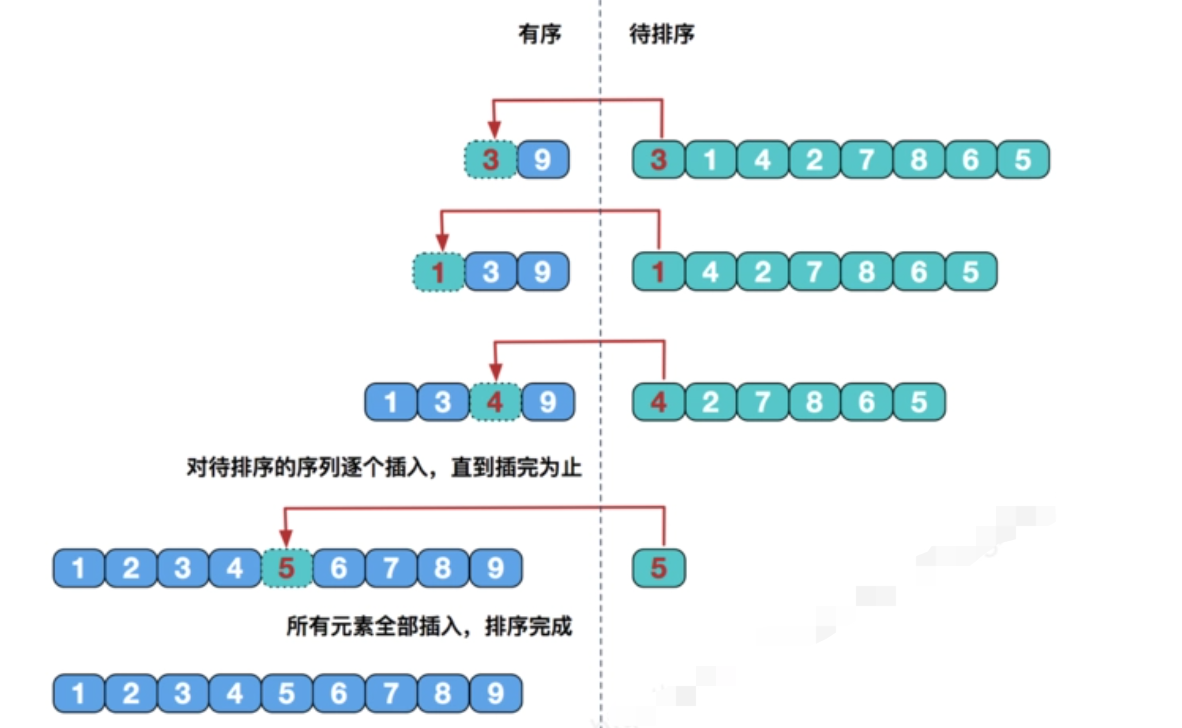
通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应的位置并插入。插入排序非常类似于整扑克牌。在开始摸牌时,左手是空的,牌面朝下放在桌上。接着,一次从桌上摸起一张牌,并将它插入到左手一把牌中的正确位置上。为了找到这张牌的正确位置,要将它与手中已有的牌从右到左地进行比较。无论什么时候,左手中的牌都是排好序的。
如果输入数组已经是排好序的话,插入排序出现最佳情况,其运行时间是输入规模的一个线性函数。如果输入数组是逆序排列的,将出现最坏情况。平均情况与最坏情况一样,其时间代价是(n2)。
public void sort(int arr[]) {
for (int i = 1; i < arr.length; i++) {
//插入的数
int insertVal = arr[i];
//被插入的位置(准备和前一个数比较)
int index = i - 1;
//如果插入的数比被插入的数小
while (index >= 0 && insertVal < arr[index]) {
//将把 arr[index] 向后移动
arr[index + 1] = arr[index];
//让 index 向前移动
index--;
}
//把插入的数放入合适位置
arr[index + 1] = insertVal;
}
}
文章来源:https://blog.csdn.net/qq_24428851/article/details/135437229
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- js中找出两个数组中不同的元素
- 目标检测数据集 - MS COCO
- 【Python机器学习系列】建立决策树模型预测心脏疾病(完整实现过程)
- 对读取的Excel文件数据进行拆分并发请求发送到后端服务器
- tkinter绘制组件(40)——滚动选值框
- SpringBoot Gateway整合过程中的问题
- LeetCode 590. N 叉树的后序遍历
- 大模型学习笔记02——大模型的能力
- 【零基础入门TypeScript】TypeScript - 运算符
- Vue3+Vite连接高德地图JS API——地图显示、输入搜索