算法——动态规划（DP，Dynamic Programming）

一、基础概念?

• DP的思想：
  • 把问题分成子问题，前面子问题的解决结果被后面的子问题使用
• DP与分治法的区别：
  • 分治法把问题分成独立的子问题，各个子问题能独立解决
    • 自顶向下
  • DP前面子问题的解决结果被后面的子问题使用，子问题间不相互独立
    • 自底向上
• 求解DP问题的步骤：
  • 1、定义状态
  • 2、状态转移?
    • 确定状态转移方程
  • 3、算法实现
• DP问题分类：
  • 1、线性DP
  • 2、非线性DP
• DP问题解决方法：
  • 顺推
  • 逆推
• DP可以解决的问题需满足三个条件：
  • 1、问题有最优解
  • 2、有大量子问题重复（DP可以把求解的结果存起来，后续用到时直接查询）
  • 3、当前阶段的求解只与前面的阶段有关，与之后的阶段无关

?二、爬楼梯（一维）

假设有级楼梯，每次只能爬1级或2级，有多少种方法可以爬到楼梯的顶部？

分析：

• 在爬上第 i 级楼梯之前 ，爬楼梯的人一定站在第 i-1 级楼梯或第 i-2 级楼梯上，两种情况
• 所以爬上第 i 级楼梯的方法等于两种走法之和（站在第i-1级楼梯，站在第i-2级楼梯上）
• 此处涉及到应用组合数学的加法规则：（“或”）
  • 如果一个事件以 a 种方式发生，第二个事件以 b 种（不同）方式发生，那么存在 a+b 种方式
• dp[i]表示爬上第i级楼梯有多少种走法
  • dp[1]=1
  • dp[2]=2
  • dp[i]=dp[i-1]+dp[i-2]，i>2（状态转移方程）

1、辅助数组

时间复杂度O(n)，空间复杂度O(n)

package no1_1;
import java.util.Scanner;
public class example {
	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		int n=sc.nextInt();
		int[] dp=new int[n+1];
		dp[1]=1;
		dp[2]=2;
		for(int i=3;i<=n;i++) {
			dp[i]=dp[i-2]+dp[i-1];
		}
		System.out.println(dp[n]);
	}
}

2、只使用两个变量记录前两项的值

时间复杂度O(n)，空间复杂度O(1)

package no1_1;
import java.util.Scanner;
public class example {
	public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		int n=sc.nextInt();
		int val1=1,val2=2,result=0;;
		for(int i=3;i<=n;i++) {//val1：前一项；val2：当前项
			result=val1+val2;
			val1=val2;
			val2=result;
		}
		System.out.println(result);
	}
}

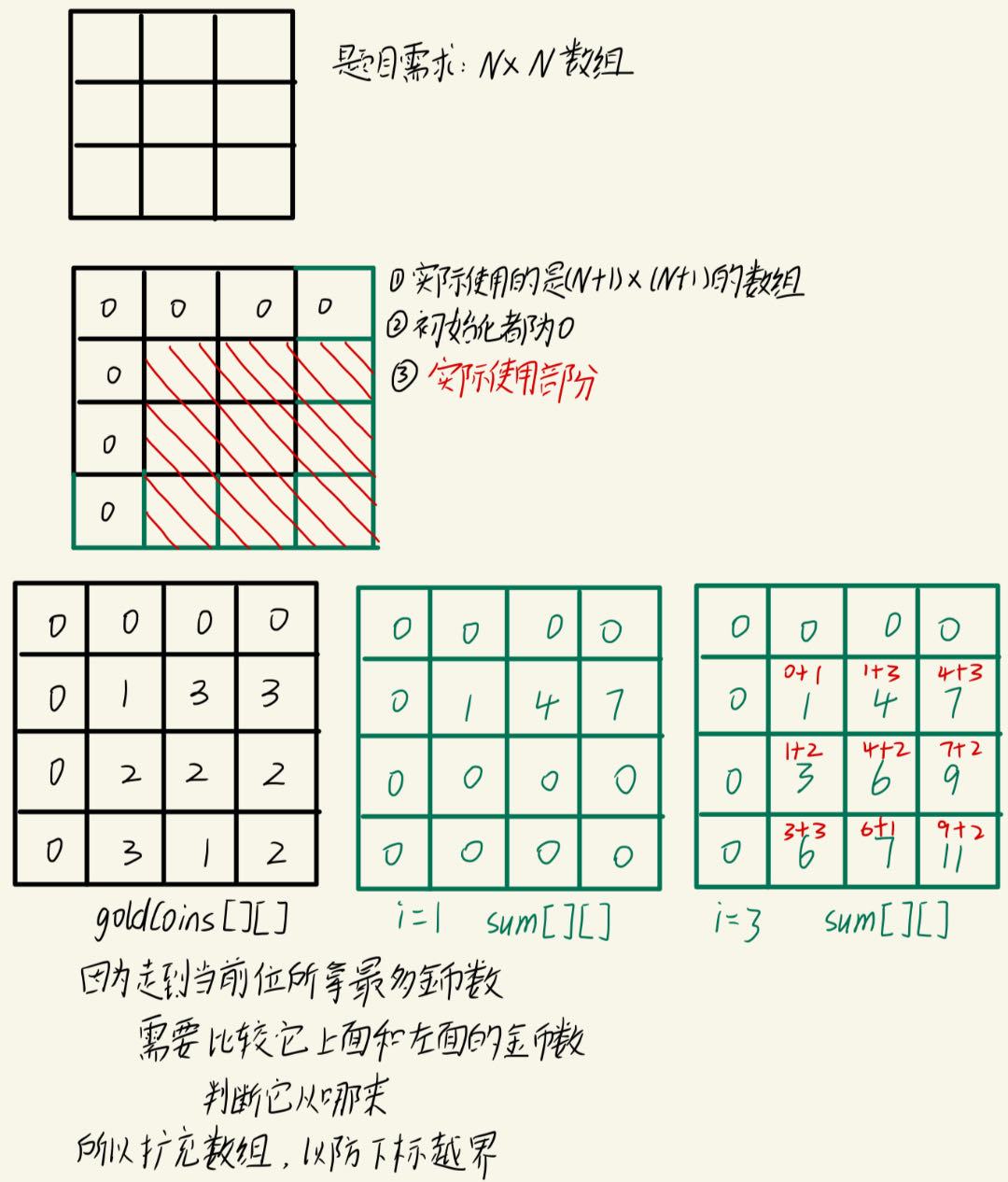
三、拿金币（二维）

有一个N x N的方格,每一个格子都有一些金币,只要站在格子里就能拿到里面的金币。你站在最左上角的格子里,每次可以从一个格子走到它右边或下边的格子里。请问如何走才能拿到最多的金币。

分析：

• 当前位的最大金币数，需要上一位也拿到最大金币数

• 

package no1_1;
import java.util.Scanner;
public class Main {
	public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		int n = scanner.nextInt();
		//根据输入，把金币放入数组中对应的位置
		int[][] goldCoins = new int[n + 1][n + 1];
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= n; j++) {
				goldCoins[i][j] = scanner.nextInt();
			}
		}
		//该数组存储的是走到当前位置所拿的最多金币数
		int[][] sum = new int[n + 1][n + 1];
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= n; j++) {
				//当前位的最大金币数，需要上一位也拿到最大金币数，
				//该循环看的是sum[i][j]，一直是往前走的，不要被i-1和j-1误了眼，觉得是倒退着走，i-1和j-1只是判断上一步是应该在哪里
				if (sum[i][j - 1] > sum[i - 1][j]) {
					sum[i][j] = sum[i][j - 1] + goldCoins[i][j];
				} else {
					sum[i][j] = sum[i - 1][j] + goldCoins[i][j];
				}
			}
		}
		
		System.out.println(sum[n][n]);
	}
}

四、印章（二维）

共有n种图案的印章，每种图案的出现概率相同。小A买了m张印章，求小A集齐n种印章的概率。

分析：

• i：买的印章数
• j：凑齐的印章数
• dp[i][j]：买了 i 个印章，凑齐了 j 种的概率
• 概率 p=1 / n?
• 情况一：
  • i < j
  • 不可能凑齐，dp[i][j]=0
• 情况二：
  • j == 1
  • 买了 i 张印章，凑齐的印章为图案1时，概率为
  • 但有 n 种印章图案，总的概率等于每个种图案的概率和（应用组合数学的加法规则 ）
  • 即，而 p = 1 / n，所以
  • 
• 情况三：

  • i >= j

  • 为下面两种情况相加（应用组合数学的加法规则）

  • 1、买了 i - 1 张 已经得到了 j 种，最后一张随便

    • dp[i] [j] = dp[i-1] [j] * ( j / n )

      • dp[i-1] [j]是买了 i - 1 张 已经得到了 j?种的概率

      • j / n是最后一张随便哪种的概率

  • 2、买了 i - 1 张 只得到了 j - 1 种，最后一张是第 j 种

    • dp[i] [j] = dp[i-1] [j-1] * （n-（j-1）） / n

      • dp[i-1] [j-1]是买了 i - 1 张 只得到了 j - 1 种的概率

      • （n-（j-1）） / n是买最后一张是第 j 种的概率

package no1_1;
import java.util.*;
public class Main {
    public static void main(String[] args) {    	
        Scanner sc=new Scanner(System.in); 
        int n=sc.nextInt();
        int m=sc.nextInt();
        double[][] array=new double[m+1][n+1];
        System.out.printf("%.4f",probability(array,n,m));//动态规划
    }
    public static double probability(double[][] array,int n,int m) {
    	double p=1.0/n;
    	for(int i=1;i<=m;i++) {//买的印章数
    		for(int j=1;j<=n;j++) {//凑齐的印章数
    			if(i<j) {//买的印章数少于种类数，不可能凑齐
    				array[i][j]=0;
    			}else if(j==1) {//只凑齐了一种
    				array[i][j]=Math.pow(p, i-1);
    			}else {
    				//为下面两种情况相加，（应用组合数学的加法规则）
    				//1、买了 i - 1 张 已经得到了 j 种，最后一张随便， dp[i] [j] = dp[i-1] [j] * ( j / n )
    				//2、买了 i - 1 张 只得到了 j - 1 种，最后一张是第 j 种， dp[i] [j] = dp[i-1] [j-1] * (n-j+1) / n
    				array[i][j]=array[i-1][j]*(j*p)+array[i-1][j-1]*((n-j+1)*p);
    			}
    		}
    	}
    	return array[m][n];
    }
}