力扣日记12.18-【二叉树篇】合并二叉树
发布时间:2023年12月18日
力扣日记:【二叉树篇】合并二叉树
日期:2023.12.18
参考:代码随想录、力扣
617. 合并二叉树
题目描述
难度:简单
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:
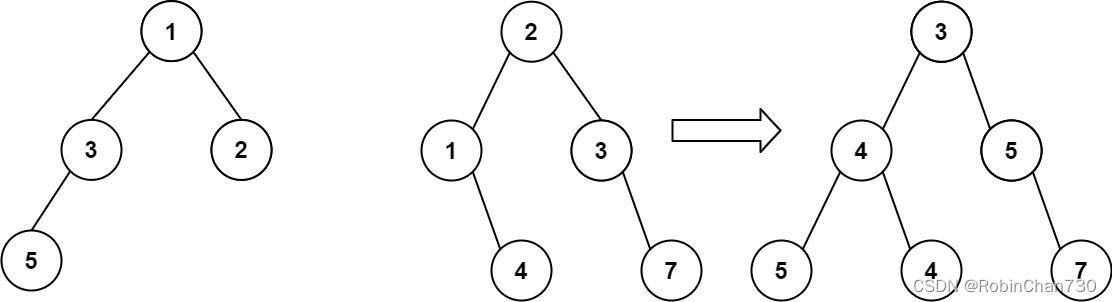
输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出:[3,4,5,5,4,null,7]
示例 2:
输入:root1 = [1], root2 = [1,2]
输出:[2,2]
提示:
- 两棵树中的节点数目在范围 [0, 2000] 内
- -10^4 <= Node.val <= 10^4
题解
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
#define SOLUTION 2
public:
#if SOLUTION == 1
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if (root1 == nullptr && root2 == nullptr) return nullptr;
if (root2 == nullptr) {
return root1;
}
if (root1 == nullptr) {
return root2;
}
traversal(root1, root2);
return root1;
}
void traversal(TreeNode* root1, TreeNode* root2) {
// 把root1当作合并后的树
root1->val = root1->val + root2->val;
// 如果root1没有左节点、root2有
if (root1->left == nullptr && root2->left != nullptr) {
// 将root2的左子树作为root1的左子树
root1->left = root2->left;
}
// 如果都有左节点(注意这里不能用if要用else if, 因为可能本来没有左节点经过上面的if语句就有了)
else if (root1->left != nullptr && root2->left != nullptr) {
// 对左子树进行递归
traversal(root1->left, root2->left);
}
// 如果root1没有右节点、root2有
if (root1->right == nullptr && root2->right != nullptr) {
// 将root2的右子树作为root1的右子树
root1->right = root2->right;
}
// 如果都有右节点(注意这里不能用if要用else if, 因为可能本来没有右节点经过上面的if语句就有了)
else if (root1->right != nullptr && root2->right != nullptr) {
traversal(root1->right, root2->right);
}
// 如果是root2->left或root2->right为空,则不需要处理
}
#elif SOLUTION == 2 // 代码随想录ver
// 输入参数为两树的根节点,返回值为合并后的节点(在tree1上进行修改)
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
// 如果 root1 为空,返回 root2
if (root1 == nullptr) return root2;
// 如果 root2 为空,返回 root1
if (root2 == nullptr) return root1;
// 如果两者不为空
// 中
root1->val += root2->val;
// 递归处理左子树的情况(将tree1左子树与tree2左子树合并,并返回合并后的左子树作为root1的左子树)
root1->left = mergeTrees(root1->left, root2->left);
// 递归处理右子树的情况
root1->right = mergeTrees(root1->right, root2->right);
return root1;
}
#endif
};
复杂度
时间复杂度:
空间复杂度:
思路总结
- 我的思路:
- 写的时候好晕,绕半天
- 本题还是得从父节点的角度去处理子节点(看两个根节点是否有左右节点)
- 这里将 root1 作为合并二叉树,需要处理①root1没有左节点而root2有左节点 或者 root1、root2都有左节点②root1没有右节点而root2有右节点 或者 root1、root2都有右节点 这些情况;对于root1有左(右)节点而root2没有,则不需处理
- 注意 if-else if 在本题需要放在恰当的位置,先用 if-else if 处理好左节点情况即①、再以相同的方式处理右节点情况即②
- 代码随想录的思路
- 看了代码随想录的解法,感觉自己的思路真是放屁,这才是真正用了合并左右子树的递归啊(我的是单纯递归处理两个根节点去了)
- 同样是在左树的基础上修改
- 这里将合并子树的根节点在每次递归返回
- 对于终止条件:
- 如果 root1 为空,此时合并后的树的 root 为 root2,返回(隐含了对 root2 为空的处理:此时返回null)
- 如果 root2 为空,此时合并后的树的 root 为 root1,返回(隐含了对 root1 为空的处理:此时返回null)
- 如果都不为空,进入递归逻辑(前序遍历):
- 中:对 左根节点的值进行修改
- 左:将 tree1和tree2的左子树合并后的根节点作为左数的左节点
- 右:将 tree1和tree2的右子树合并后的根节点作为左数的右节点
- 最终返回合并后的左数根节点root1
- 迭代:
- 使用队列,模拟层序遍历
- 迭代法中,一般一起操作两个树都是使用队列模拟类似层序遍历,同时处理两个树的节点
- // TODO
文章来源:https://blog.csdn.net/weixin_45847708/article/details/135072726
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 唇炎治疗文章——的相关回答
- 2023/12/17 初始化
- Gitlab Gitee GitHub 远程仓库显示图片
- 51-15 视频理解串讲—TimeSformer论文精读
- 《Vue2 进阶知识》动态挂载组件之Vue.extend + vm.$mount
- 通付盾APP尽职调查报告正式挂牌上海数据交易所
- 年终关账四大财务处理技巧|柯桥会计做账,财税知识
- 某商业银行薪酬体系设计项目成功案例纪实
- 极兔单号查快递,极兔快递单号查询,筛选出途经指定城市的单号
- 全光谱护眼灯哪个牌子好?全光谱备考护眼台灯推荐