前菜---二叉树+堆的小练习

目录
前言🏜?
之前的博客,我们一起学习了二叉树的概念和性质,堆的实现,如何实现二叉树的链式结构。今天,我们来复习总结一下二叉树的性质,并且做一些练习题来巩固一下知识点,为后面的oj题打下基础。
对之前内容不了解的活着忘记了的,可以点击下方链接🔗:
1. 二叉树性质总结??
1.?若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 2^ (n-1)个结点.
2.?若规定根节点的层数为1,则深度为h的二叉树的最大结点数是 2^h - 1.
3.?对任何一棵二叉树,?如果度为0其叶结点个数为 n0,?度为2的分支结点个数为 n2,则有 n0= n2+1
4.?若规定根节点的层数为1,具有n个结点的满二叉树的深度,h= log2(n+1).
5.?对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
1)?若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
2)?若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
3)?若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
除了性质3我们没介绍过,其他的我们在之前的博客就介绍过了,需要的小伙伴点击下方链接🔗:
1.2 性质3?

2. 二叉树性质小练习🏕?
1.?某二叉树共有?399?个结点,其中有?199?个度为?2?的结点,则该二叉树中的叶子结点数为( )
A?不存在这样的二叉树
B 200
C 198
D 199
2.下列数据结构中,不适合采用顺序存储结构的是( )
A?非完全二叉树
B?堆
C?队列
D?栈
3.在具有?2n?个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
4.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
3. 答案+解析💡
1.解析:根据性质3可知,n0=n2+1;所以度为0的节点(叶子节点)个数为200
答案:B
2.解析:非完全二叉树用链式结构存储更好,不会造成空间浪费
答案:A
3.解析:由性质3可知,n0=n2+1;假设度为0的节点有n0个,度为1的节点有n1个,度为2的节点有n2个;所以,n2+1+n1+n2=2n;在完全二叉树中度为1的节点有0个or1个,这里2n肯定是偶数,那么倒推出来n1=1,这样才能保证等式成立;所以n0=n2+1=n
答案:A
4.解析:h的范围[log2N + 1 ,log2(N+1)];将N=531代入,可求得h范围
答案:B
4. 堆概念结构小练习🪔
1.下列关键字序列为堆的是:()
A?100,60,70,50,32,65
B?60,70,65,50,32,100
C?65,100,70,32,50,60
D?70,65,100,32,50,60
E?32,50,100,70,65,60
F?50,100,70,65,60,32
2.已知小根堆为8,15,10,21,34,16,12,删除关键字?8?之后需重建堆,在此过程中,关键字之间的比较次数是()。
A?1
B?2
C?3
D?4
3.小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后,其结果是()
A[3,2,5,7,4,6,8]
B[2,3,5,7,4,6,8]
C[2,3,4,5,7,8,6]
D[2,3,4,5,6,7,8]
5. 答案+解析🧿
1.解析:根据大小堆2种形式:大堆:父>=子 ? 小堆:父<=子
答案:A
2.解析:首尾交换,删除关键字8,向下调整3次(总共3层)
答案:C
3.解析:首尾交换,删除堆尾元素,向下调整
答案:C
6. 前/中/后/层序遍历小练习🔫
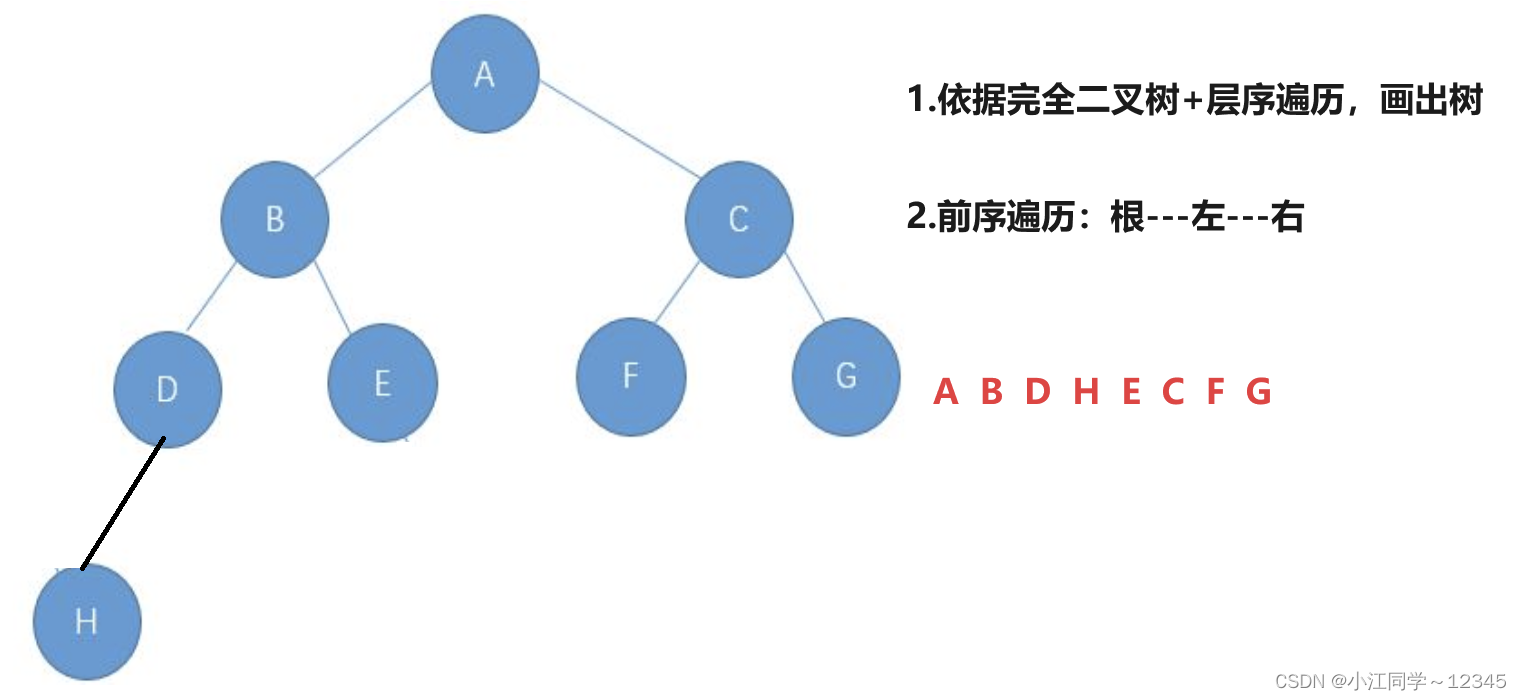
1.某完全二叉树按层次输出(同一层从左到右)的序列为?ABCDEFGH?。该完全二叉树的前序序列为( )
A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
A E
B F
C G
D H
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为____。
A adbce
B decab
C debac
D abcde
4.某二叉树的后序遍历序列与中序遍历序列相同,均为?ABCDEF?,则按层次输出(同一层从左到右)的序列为()
A FEDCBA?
B CBAFED
C DEFCBA
D ABCDEF
7. 答案+解析🧺
1.解析:
答案:A
2.解析:先序遍历,先遍历根节点--->E就是根节点
答案:A
3.解析:
答案:D
4.解析:
答案:A
后语🌋
到这里,我们的小练习就已经全部写完了。如果有别的思路或者疑问,欢迎在评论区提出,大家一起讨论讨论!!!
下篇博客,我们就要想二叉树的oj题进军了!!!
本次的分享到这里就结束了!!!
PS:小江目前只是个新手小白。欢迎大家在评论区讨论哦!有问题也可以讨论的!期待大家的互动!!!
公主/王子殿下,请给我点赞👍+收藏??+关注?(这对我真的很重要!!!)

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Halcon计算最小外接矩形Smallest_rectangle2
- 运筹说 第95期 | 非线性规划奠基人——库恩与塔克
- MySQL锁机制与优化实践
- scikit-learn文档中的数据生成器
- HTTP响应头未设置‘Content-Security-Policy‘
- Python学习笔记之(一)搭建Python 环境
- Windows+Qt5.14.2+android x86配置(待完善)
- dataframe如何修改列名
- 黑马学成在线项目bug记录
- LeetCode 145. 二叉树的后序遍历