电路分析 第三章（线性电阻电路的一般分析法）

一、KCL、KVL方程的独立性

1、电路的图

（1）电路的图由点和线段构成，每一个点对应着电路中的一个节点，每条线段对应着电路中的一条支路。通常将图中的点和线段直接称为节点和支路。电路的图仅反映电路的拓扑结构，不能反映各支路的元件特性。

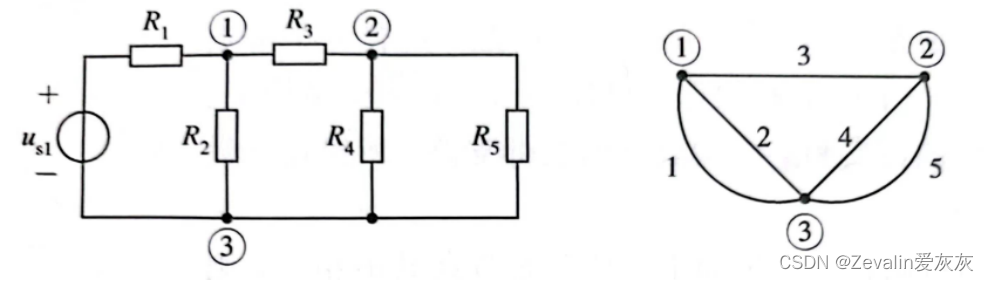
（2）若一条路径的起始节点和终止节点为同一个节点，则称为闭合路径，又称为回路。平面电路中，内部不包含支路的回路称为网孔（通俗地说就是“最小回路”）。

2、两个方程的独立性

（1）如果说某方程独立于其它方程，意思就是它不能由其它方程变换而得。

（2）KCL方程的独立性：对于有n个节点的网络，可得到n-1个独立的节点KCL方程，与这些独立方程对应的节点称为独立节点，电路中任意选定的n-1个节点都是独立节点。

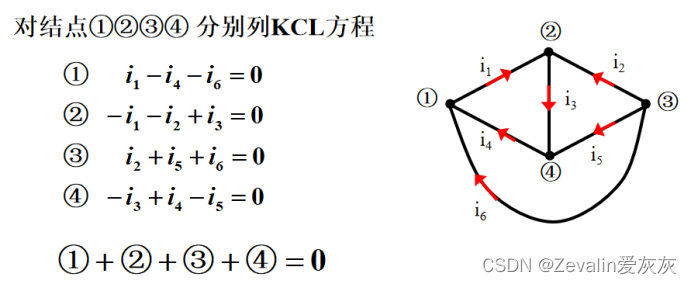
（3）KVL方程的独立性：对于有n个节点、b条支路的电路，可得到l=b-(n-1)个独立的回路KVL方程，与这些独立方程对应的回路称为独立回路。

①平面电路中有l个网孔，它们是一组独立回路。

②独立回路的选择有多种方法，对平面电路而言，网孔是一种直观而方便的选择。另一种常用的方法是每选一个回路，都包含一条新支路，选满l个为止。

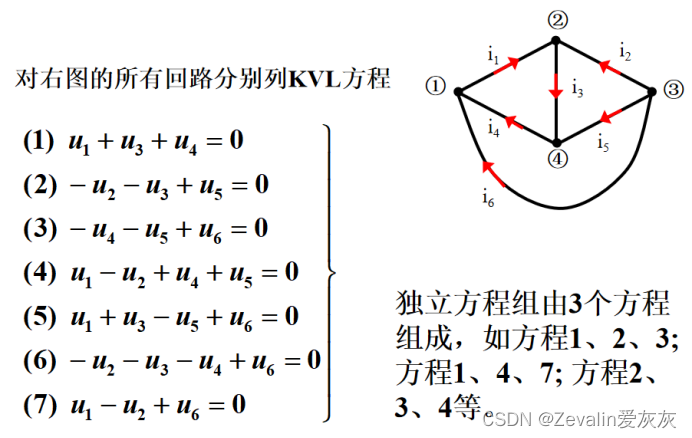
（4）综上所述，对于有n个节点、b条支路的电路，可得到独立的KCL、KVL方程共b个。

二、支路电流法

支路电流法是以各支路电流为未知量列电路方程分析电路的方法。

1、支路电流法的一般步骤

（1）标定各支路电流（电压）的参考方向。

（2）对于有n个结点、b条支路的电路，要求解支路电流，未知量共有b个，只要列出b个独立的电路方程，便可以求解这b个变量。

①从电路的n个结点中任意选择n-1个结点列写KCL方程。

②选择b-(n-1)个独立回路列写KVL方程，方程中电阻上电压用支路电流表示。

（3）求解上述方程，得到b个支路电流。

（4）进一步计算支路电压和进行其它分析。

2、支路电流法的应用举例和说明

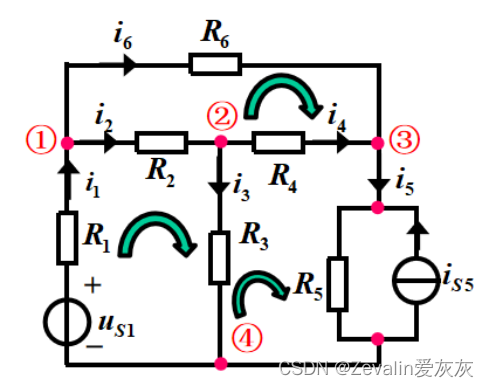
（1）经过上述的第三个步骤，可得到形式的方程组。

（2）是回路中第k个支路电阻上的电压。当参考方向与回路方向一致时取“+”，否则取“-”。

（3）为回路中第k支路的电源电压，包括电压源电压，也包括电流源引起的电压。当参考方向与回路方向一致时取“-”，否则取“+”。

3、方程列写思路plus

（1）对含有理想电流源的电路，列写支路电流方程有两种方法：

①设电流源两端电压，把电流源看作电压源来列写方程，然后增补一个方程，即令电流源所在支路电流等于电流源的电流即可。

②避开电流源所在支路列方程，把电流源所在支路的电流作为已知。

（2）对含有受控源的电路，一般将受控源视作独立源处理，同时分两种情况作进一步处理：

①如受控源的控制量是某支路电流，此时就无须再针对受控源的控制量列写辅助方程。

②如受控源的控制量是某支路电压，此时就必须列写辅助方程，将控制量用支路电流来表示。

三、节点电压法

节点电压法是以节点电压为未知量列写电路方程分析电路的方法，适用于节点较少的电路，另外该方法还适用于立体电路。

1、节点电压和节点电压法

（1）若电路中有n个节点，任选其中n-1个节点为独立节点，剩下的一个非独立节点作为参考节点，其余节点对参考节点之间的电压就是节点电压，节点电压的参考方向由独立节点指向参考节点。一般将选定的参考节点用符号“⊥”表示。

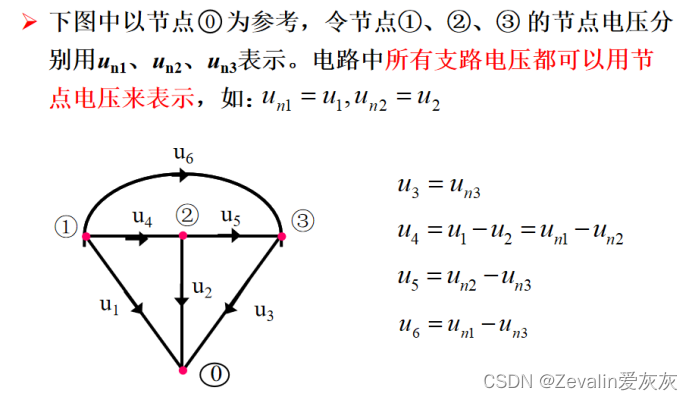
（2）由基尔霍夫电压定律可知，任意两个独立节点间的电压等于该两点电位（即节点电压）之差，若将参考节点看作零电位点，则节点电压就是各独立节点的电位。

（3）选节点电压为未知量，则KVL自动满足，就无需列写KVL方程。各支路电流、电压可视为节点电压的线性组合，求出节点电压后，便可方便地得到各支路电压、电流。

（4）节点电压法列写的是节点上的KCL方程，于含有b条支路和n个节点的平面电路，列出的独立方程数为n-1，与支路电流法相比，方程数减少b-(n-1)个。

2、节点电压法的一般步骤

（1）电路中有n个节点，任选其中n-1个节点为独立节点，剩下的一个非独立节点作为参考节点，其余节点对参考节点之间的电压就是节点电压，通常以参考节点为各节点电压的负极性。

（2）对n-1个独立节点，以节点电压为未知量，各支路电压用节点电压的线性组合表示，列写其KVL方程。

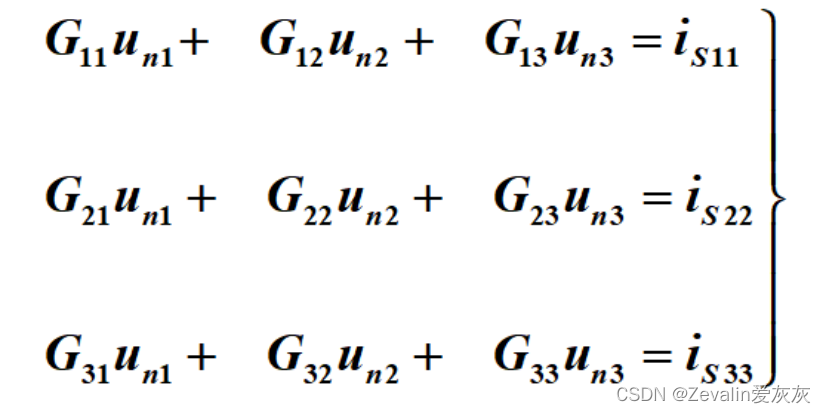
①与节点相连的各支路电导之和称为节点的自导，如上示方程中的；自导总是正的。连接于两节点间支路电导的负值是节点间的互导，如上示方程中的；互导总是负的。

②是节点电压对节点k上各电导流出的电流之和，是节点电压对节点k上各电导流出的电流之和。

③是流入节点k的注入电流，注入电流等于流向节点的电源电流的代数和，流入节点者前面取“＋”号，流出节点者前面取“－”号。

④与电流源串接的电阻不参与列方程。

（3）求解上述方程，得到n-1个节点电压。

（4）各支路电压可用节点电压的线性组合表示，根据节点电压求各支路电压。

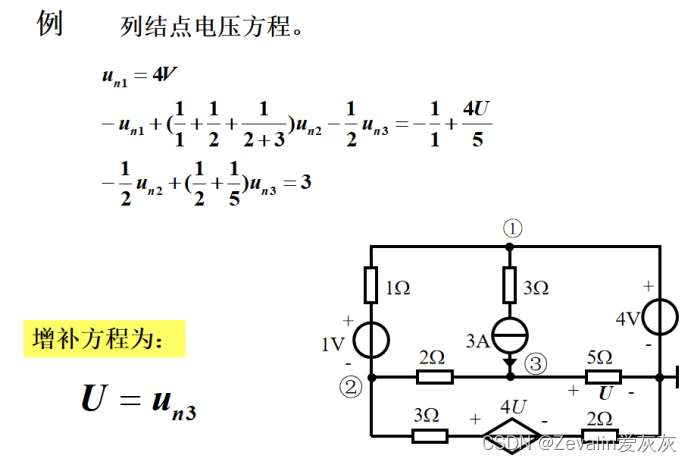
3、节点电压法的应用举例和说明

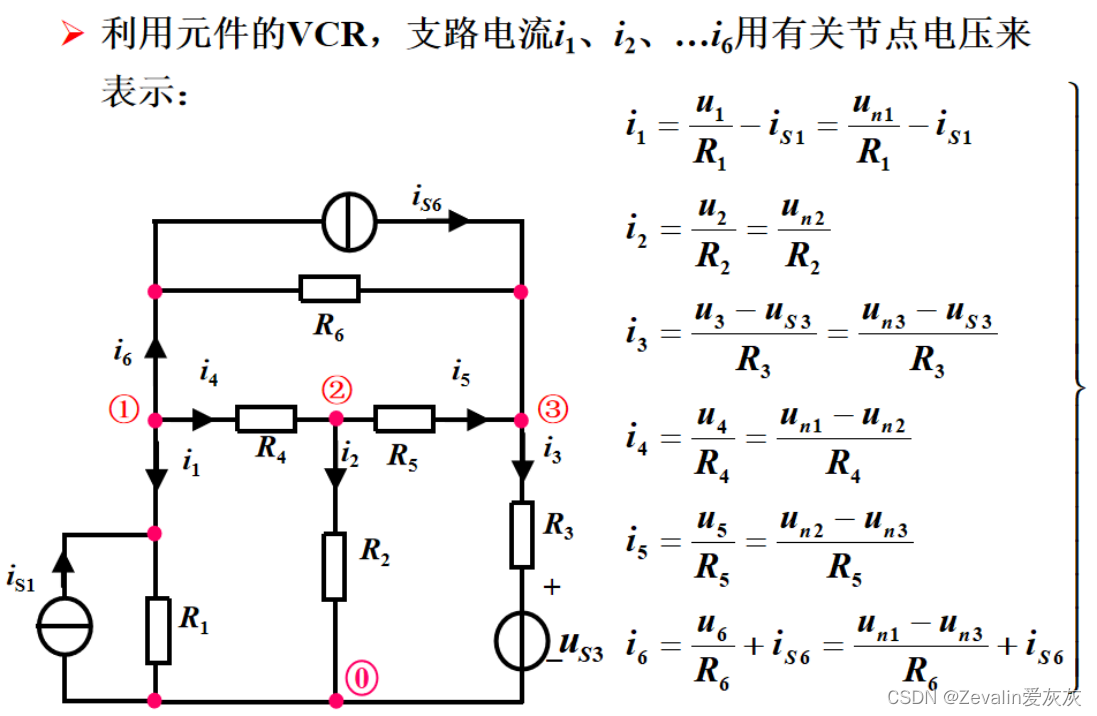
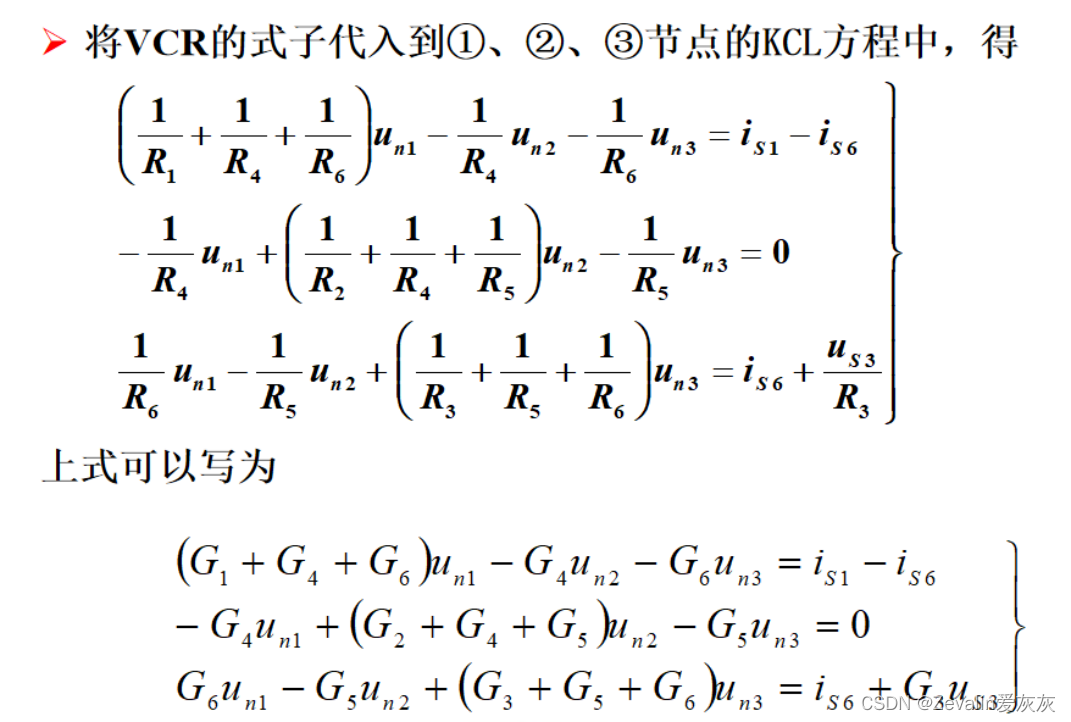
节点①的自导为，节点②的自导为，节点③的自导为，节点①和节点②的互导为，节点①和节点③的互导为，节点②和节点②的互导为。

4、方程列写思路plus

（1）当电路中含有无伴电压源支路（该支路上没有电阻与电压源串联）时，这时可以采用以下措施：

①尽可能取电压源支路的负极性端作为参考点。

②把电压源中的电流作为变量列入节点方程，并将其电压与两端节点电压的关系作为补充方程一并求解。

③将连接无伴电压源的两个节点的节点电压方程合为一个，即取一个包含这两节点的封闭面的KCL，可避免附加电流变量的出现。

（2）如理想电压源与电阻串联时，可将这样的组合等效为理想电流源与电阻的并联组合，进而运用节点电压法。

（3）当电路中有受控电流源时，在建立节点电压方程时，先把控制量用节点电压表示，并暂时把它当作独立电流源，按上述方法列出节点电压方程，然后把用节点电压表示的受控电流源电流移到方程的左边。

①当电路中存在有伴受控电压源时，把控制量用有关节点电压表示并变换为等效受控电流源。

②如果有无伴受控电压源时，可参照独立电压源的处理方法。

四、网孔电流法

网孔电流法是以独立回路中的网孔电流为未知量列写电路方程分析电路的方法。

1、网孔电流与网孔电流法

（1）假设每个网孔分别有一个环形电流流动，将这种沿网孔流动的假想电流称为网孔电流，各支路电流等于流经该支路的网孔电流的代数和。网孔电流在独立回路中是闭合的，对每个相关节点均流进一次、流出一次，所以KCL自动满足。

（2）网孔电流法是对独立回路列写KVL方程，对于含有b条支路和n个节点的平面电路，列出的独立方程数为b-(n-1)，与支路电流法相比，方程数减少n-1个。

2、网孔电流法的一般步骤

（1）一个含有b条支路和n个节点的平面电路有m=b-(n-1)个网孔，选定m个独立网孔，并确定其绕行方向。

（2）对m个独立网孔，以网孔电流为未知量，各支路电流用网孔电流的线性组合表示，列写其KVL方程。

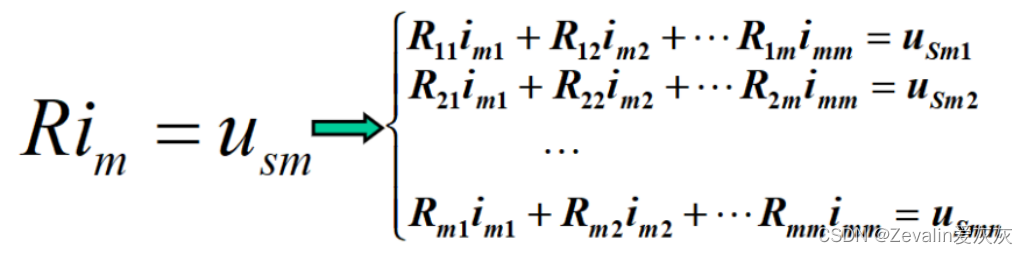
①是回路k的网孔电流。

②回路k的自阻（自阻可认为是回路中的电阻阻值之和），自阻总是为正；是回路j和回路k之间的互阻（互阻可认为是同时处于两个回路中的电阻），流过互阻的两个回路电流方向相同时互阻为正，流过互阻的两个回路电流方向相反时互阻为负。

③是回路k中所有电压源电压的代数和，当电压源电压方向与该回路方向一致时，取“－”，反之取“＋”。

（3）求解上述方程，得到m个网孔电流。

（4）各支路电流可用网孔电流的线性组合表示，根据网孔电流求各支路电流。

3、网孔电流法的应用举例和说明

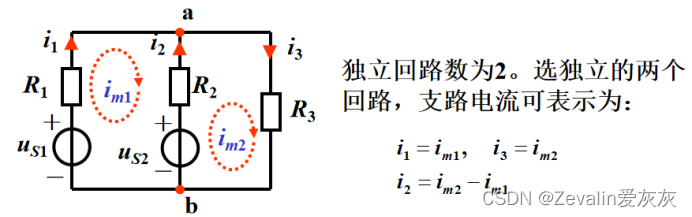
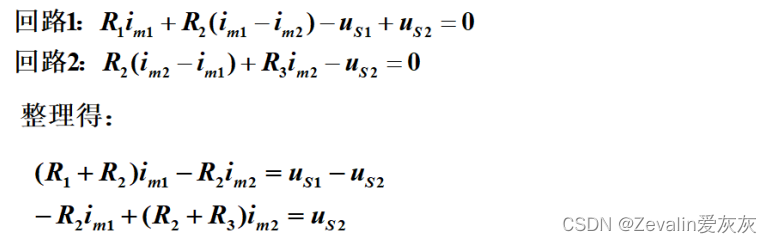
是回路1的自阻，是回路2的自阻，是回路1和回路2之间的互阻。

4、方程列写思路plus

（1）对含有理想电流源的电路：

①引入电流源电压，把电流源看作电压源列方程，并增加回路电流和电流源电流的关系方程。

②选取独立回路，使理想电流源支路仅仅属于一个回路（如下图所示），该回路电流即。

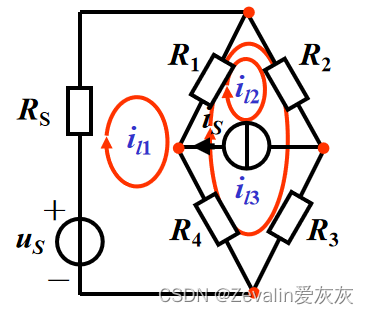
③与电阻并联的电流源，可做电源等效变换将其“变成”电压源。

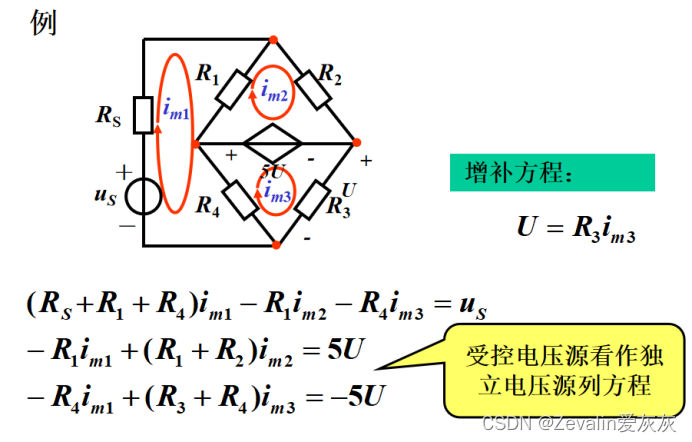
（2）对含有受控电源支路的电路，可先把受控源看作独立电源按上述方法列方程，再将控制量用回路电流表示。