sklearn 逻辑回归Demo
逻辑回归案例
假设表示
基于上述情况，要使分类器的输出在[0,1]之间，可以采用假设表示的方法。
设
h
θ
(
x
)
=
g
(
θ
T
x
)
h_θ (x)=g(θ^T x)
hθ?(x)=g(θTx)，
其中
g
(
z
)
=
1
(
1
+
e
?
z
)
g(z)=\frac{1}{(1+e^{?z} )}
g(z)=(1+e?z)1?, 称为逻辑函数（Sigmoid function，又称为激活函数，生物学上的S型曲线）
h
θ
(
x
)
=
1
(
1
+
e
?
θ
T
X
)
h_θ (x)=\frac{1}{(1+e^{?θ^T X} )}
hθ?(x)=(1+e?θTX)1?
其两条渐近线分别为h(x)=0和h(x)=1
在分类条件下，最终的输出结果是：
h
θ
(
x
)
=
P
(
y
=
1
│
x
,
θ
)
h_θ (x)=P(y=1│x,θ)
hθ?(x)=P(y=1│x,θ)
其代表在给定x的条件下 其y=1的概率
P ( y = 1 │ x , θ ) + P ( y = 0 │ x , θ ) = 1 P(y=1│x,θ)+P(y=0│x,θ)=1 P(y=1│x,θ)+P(y=0│x,θ)=1
决策边界（ Decision boundary）
对假设函数设定阈值
h
(
x
)
=
0.5
h(x)=0.5
h(x)=0.5，
当
h
(
x
)
≥
0.5
h(x)≥0.5
h(x)≥0.5 时，输出结果y=1.
根据假设函数的性质，当
x
≥
0
时，
x≥0时，
x≥0时，h(x)≥0.5
用
θ
T
x
θ^T x
θTx替换x，则当
θ
T
x
≥
0
θ^T x≥0
θTx≥0时，
h
(
x
)
≥
0.5
，
y
=
1
h(x)≥0.5，y=1
h(x)≥0.5，y=1
解出 θ T x ≥ 0 θ^T x≥0 θTx≥0，其答案将会是一个在每一个 x i x_i xi?轴上都有的不等式函数。
这个不等式函数将整个空间分成了y=1 和 y=0的两个部分，称之为决策边界。
激活函数的代价函数
在线性回归中的代价函数：
J
(
θ
)
=
1
m
∑
i
=
1
m
1
2
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
2
J(θ)=\frac{1}{m}∑_{i=1}^m \frac{1}{2} (h_θ (x^{(i)} )?y^{(i)} )^2
J(θ)=m1?i=1∑m?21?(hθ?(x(i))?y(i))2
令
C
o
s
t
（
h
θ
(
x
)
，
y
）
=
1
2
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
2
Cost（hθ (x)，y）=\frac{1}{2}(h_θ (x^{(i)} )?y^{(i)} )^2
Cost（hθ(x)，y）=21?(hθ?(x(i))?y(i))2，
Cost是一个非凹函数，有许多的局部最小值，不利于使用梯度下降法。对于分类算法，设置其代价函数为：
J
(
θ
)
=
?
1
m
∑
i
=
1
m
[
y
(
i
)
l
o
g
(
h
θ
(
x
(
i
)
)
)
?
(
1
?
y
(
i
)
)
?
l
o
g
(
1
?
h
θ
(
x
(
i
)
)
)
]
J(θ)=-\frac{1}{m}∑_{i=1}^m [y^{(i)}log(h_θ (x^{(i)}) )?(1-y^{(i)})*log(1-h_θ (x^{(i)}))]
J(θ)=?m1?i=1∑m?[y(i)log(hθ?(x(i)))?(1?y(i))?log(1?hθ?(x(i)))]
对其化简：
C
o
s
t
（
h
θ
(
x
)
,
y
）
=
?
y
l
o
g
(
h
θ
(
x
)
)
?
(
(
1
?
y
)
l
o
g
?
(
1
?
h
θ
(
x
)
)
)
Cost（h_θ (x),y）=?ylog(h_θ (x))?((1?y)log?(1?h_θ (x)))
Cost（hθ?(x),y）=?ylog(hθ?(x))?((1?y)log?(1?hθ?(x)))
检验：
当
y
=
1
y=1
y=1时，
?
l
o
g
?
(
h
θ
(
x
)
)
?log?(h_θ (x))
?log?(hθ?(x))
当
y
=
0
y=0
y=0时，
?
l
o
g
?
(
1
?
h
θ
(
x
)
)
?log?(1?h_θ (x))
?log?(1?hθ?(x))
那么代价函数可以写成：
J
(
θ
)
=
?
1
m
[
∑
i
=
1
m
y
(
i
)
l
o
g
?
(
h
θ
(
x
(
i
)
)
)
+
(
1
?
y
(
i
)
)
l
o
g
(
1
?
h
θ
(
x
(
i
)
)
)
]
J(θ)=-\frac{1}{m}[∑_{i=1}^m y^{(i)} log?(h_θ(x^{(i)} ))+(1?y^{(i)}) log(1?h_θ (x^{(i)}))]
J(θ)=?m1?[i=1∑m?y(i)log?(hθ?(x(i)))+(1?y(i))log(1?hθ?(x(i)))]
对于代价函数，采用梯度下降算法求θ的最小值：
θ
j
?
θ
j
?
α
?
J
(
θ
)
?
θ
j
θ_j?θ_j?α\frac{?J(θ)}{?θ_j}
θj?:=θj??α?θj??J(θ)?
代入梯度：
θ
j
?
θ
j
?
α
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
x
j
i
θ_j?θ_j?α∑_{i=1}^m(h_θ (x^{(i)} )?y^{(i)} ) x_j^i
θj?:=θj??αi=1∑m?(hθ?(x(i))?y(i))xji?
sklearn 代码
导入库
## 基础函数库
import numpy as np
## 导入画图库
import matplotlib.pyplot as plt
## 导入逻辑回归模型函数
from sklearn.linear_model import LogisticRegression
模型训练
## 构造数据集
x_fearures = np.array([[-1, -2], [-2, -1], [-3, -2], [1, 3], [2, 1], [3, 2]])
y_label = np.array([0, 0, 0, 1, 1, 1])
## 调用逻辑回归模型
lr_clf = LogisticRegression()
## 用逻辑回归模型拟合构造的数据集
lr_clf = lr_clf.fit(x_fearures, y_label) #其拟合方程为 y=w0+w1*x1+w2*x2
模型参数查看
## 查看其对应模型的w
print('the weight of Logistic Regression:',lr_clf.coef_)
## 查看其对应模型的w0
print('the intercept(w0) of Logistic Regression:',lr_clf.intercept_)
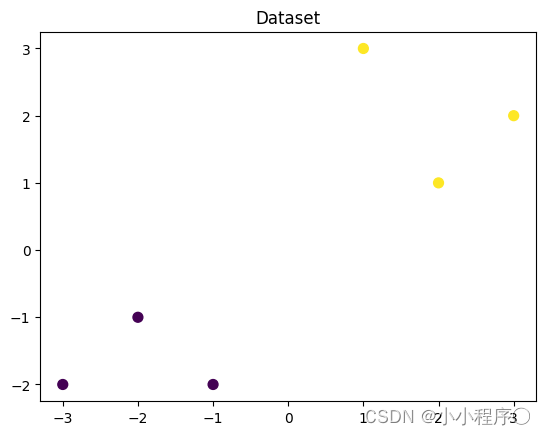
可视化构造的数据样本点
plt.figure()
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')
plt.show()
模型预测
## 在训练集和测试集上分别利用训练好的模型进行预测
y_label_new1_predict = lr_clf.predict(x_fearures_new1)
y_label_new2_predict = lr_clf.predict(x_fearures_new2)
print('The New point 1 predict class:\n',y_label_new1_predict)
print('The New point 2 predict class:\n',y_label_new2_predict)
## 由于逻辑回归模型是概率预测模型（前文介绍的 p = p(y=1|x,\theta)）,所以我们可以利用 predict_proba 函数预测其概率
y_label_new1_predict_proba = lr_clf.predict_proba(x_fearures_new1)
y_label_new2_predict_proba = lr_clf.predict_proba(x_fearures_new2)
print('The New point 1 predict Probability of each class:\n',y_label_new1_predict_proba)
print('The New point 2 predict Probability of each class:\n',y_label_new2_predict_proba)
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！