50. Pow(x, n)(Leetcode) C++递归实现（超详细）

---

前言

在本文章中，我们将要详细介绍一下Leetcode中第50题， Pow(x, n)的内容

一、题目分析

题目要求很简单：我们模拟实现一个pow函数。

二、算法原理

1.递归分析

🏉🏉我们按照正常思路，放在循环里一个个乘起来就可以。
我们来实现以下看一下是否可行！！！

class Solution {
public:
    double myPow(double x, int n) 
    {
        int tmp=n;
        if(n<0) n=-n;
        double ret=1.0;
        for(int i=0;i<n;i++)
        {
            ret*=x;
        }
        return tmp<0? (1.0/ret):ret;
    }
};

我们发现超出了时间限制，时间复杂度O（N）

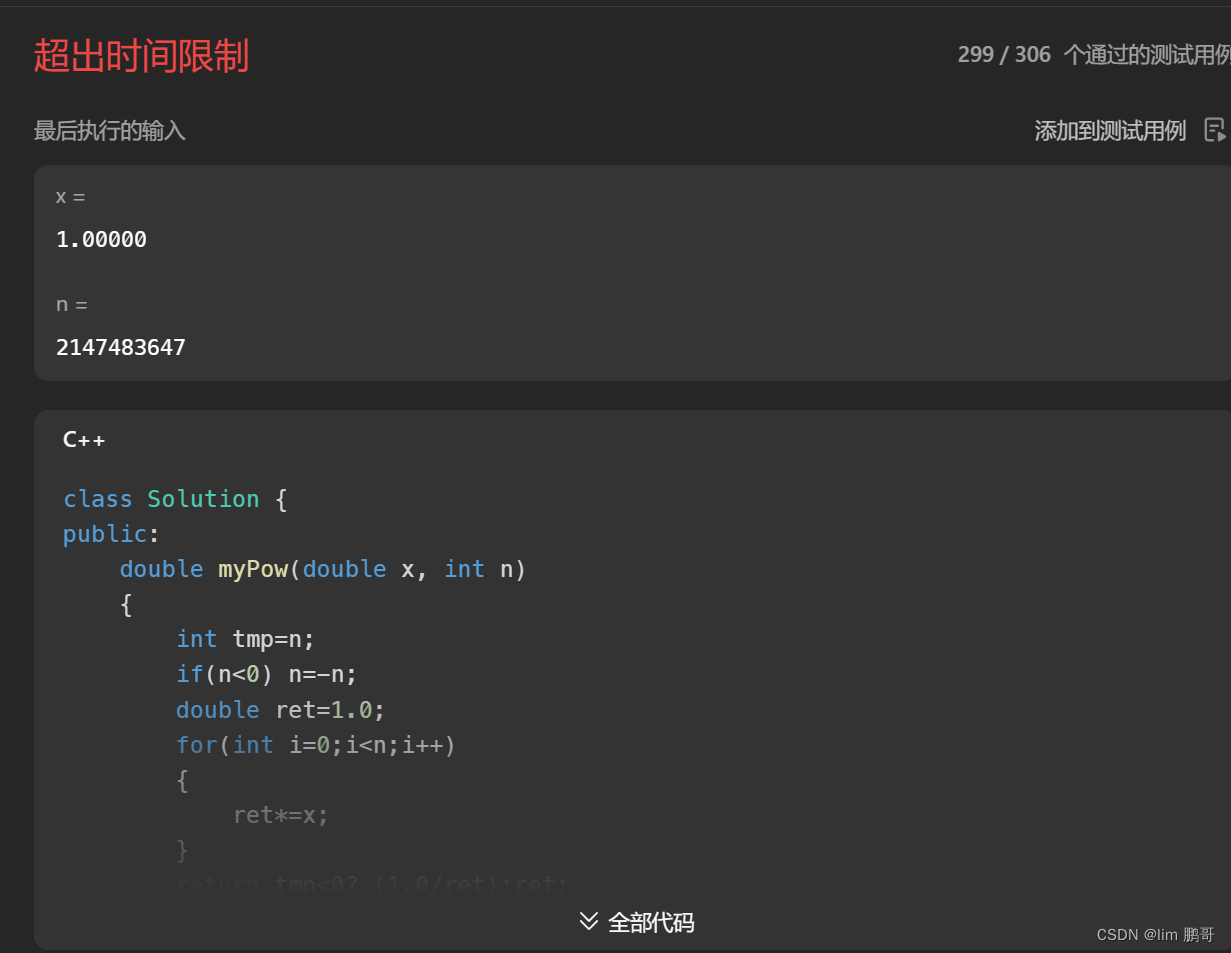
🏉🏉我们来看一种全新的算法–-快速幂

我们来一看具体是什么
? 比如我们要求2^17 , 我们可以先求2^8， 利用两个2^8相乘再乘一次8就得到了2 ^17;
? 同样的道理，我们求2 ^8,先求2 ^4, 利用两个2^4相乘就得到了2 ^8;
? 当我们求到2^1，先求2 ^0,利用两个2 ^0 相乘再乘以个2，就得到了

我们发现了重复子问题，当次方数为奇数时，我们多乘一次就可以。

2.递归实现

💝💝.相同子问题---->函数头
我们就是根据两个参数，一个是次幂数，一个是要进行次幂的数，返回结果
double pow(double x,int n);
💝💝.只关心某个子问题的求解过程—>函数体
我们先求出递归后结果tmp，
然后判断n的奇偶数，分情况讨论。返回结果
💝💝.递归出口
当n==0时，不在往下分，返回结果

同时还要考虑n为负数的情况

三、代码实现+复杂度分析

我们来实现一下代码

class Solution {
public:
    double myPow(double x, int n) 
    {
       return n<0?1.0/pow(x,-n):pow(x,n);
    }
    double pow(double x,int n)
    {
        if(n==0)
        {
            return 1.0;
        }
        double tmp=pow(x,n/2);
        if(n%2==1)
        {
            return tmp*tmp*x;
        }
        else
        {
            return tmp*tmp;
        }
    }
};

我们发现还是有错误

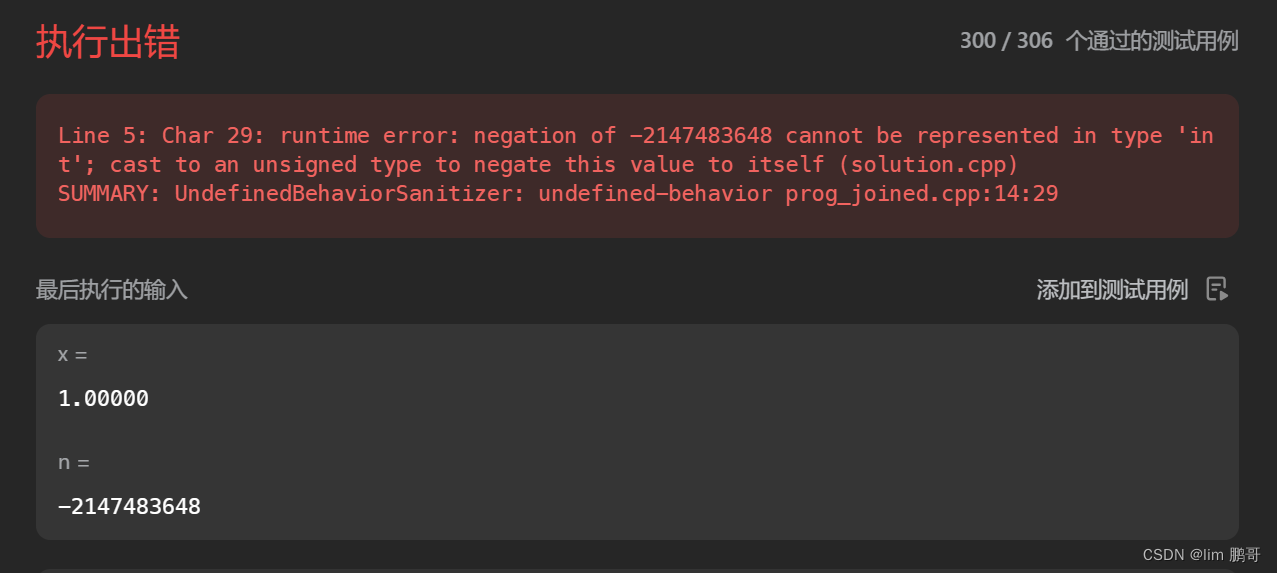
🎁🎁我们知道int的类型范围是-2^31 -----2^31-1
当n=-2^31,我们把它转化为正数计算，随后再用1去除以这个数据

2^31已经超过了整形的范围，我们需要进行类型转化，转化成为long long

class Solution {
public:
    double myPow(double x, int n) 
    {
       return n<0?1.0/pow(x,-(long long)n):pow(x,n);
    }
    double pow(double x,long long n)
    {
        if(n==0)
        {
            return 1.0;
        }
        double tmp=pow(x,n/2);
        if(n%2==1)
        {
            return tmp*tmp*x;
        }
        else
        {
            return tmp*tmp;
        }
    }
};

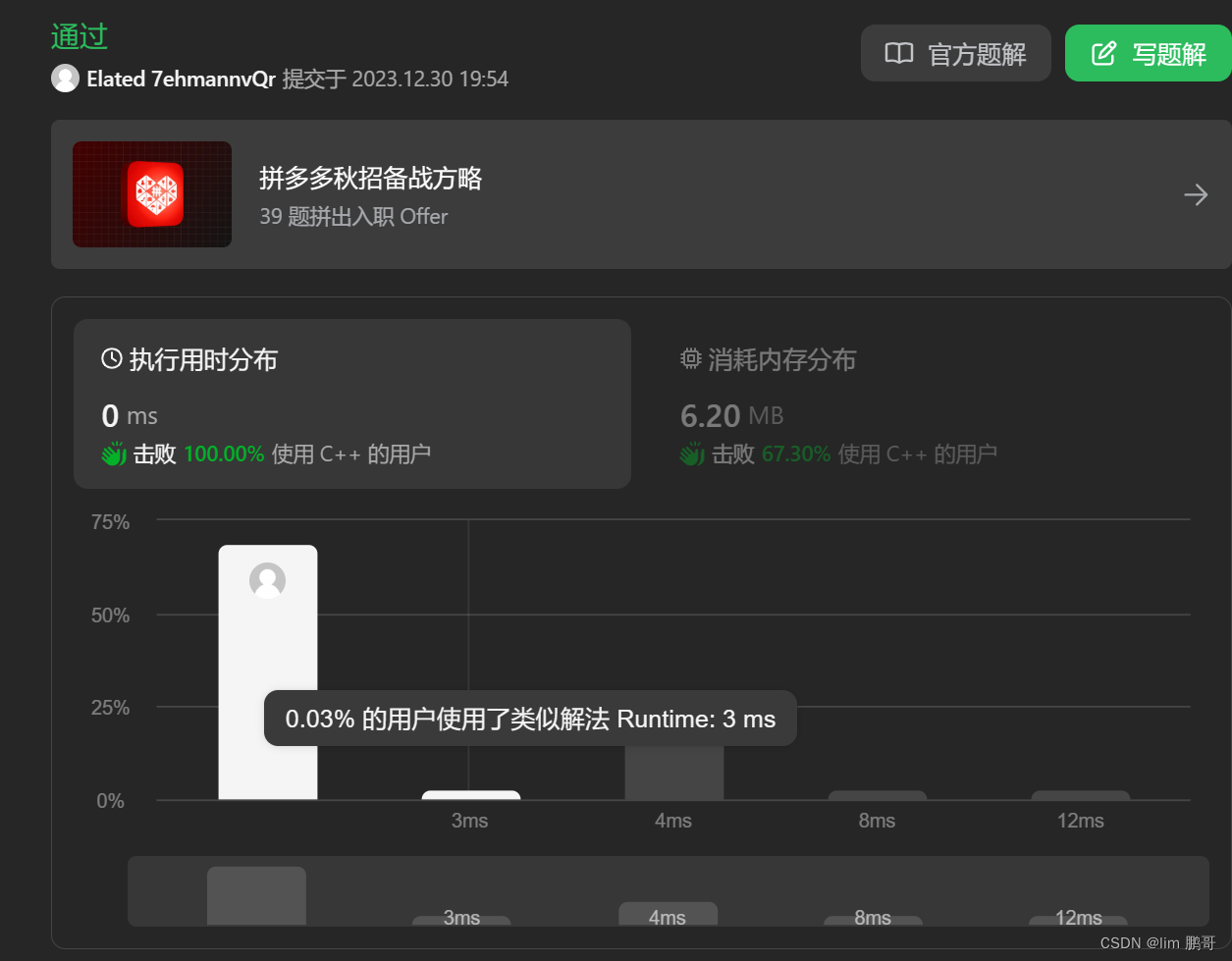
时间复杂度O（logN）
空间复杂度O（logN）

总结

以上就是我们对Leetcode中第50道题目 Pow(x, n)详细介绍，希望对大家的学习有所帮助，仅供参考 如有错误请大佬指点我会尽快去改正 欢迎大家来评论~~