流量预测中文文献阅读（郭郭专用）

基于流量预测的超密集网络资源分配策略研究_2023_高雪亮_内蒙古大学

（1）内容总结

这篇文章从预测的角度来分析并研究动态资源分配策略，使用米兰数据集，对时空维度的数据进行流量预测CDR，采用卷积模块，时间嵌入模块（？），注意力模块。在流量预测的基础上，实现了信道资源按需分配，即每个小基站按照其覆盖区域下的流量大小比例分配子信道资源。基站的信道资源采用图论的最大团方法进行分配。每个小基站的资源分配给用户采用动态子信道分配策略，最大化用户满意度。

（2）流量预测部分

1、数据集

意大利电信，米兰市：总结中有链接here
在原数据集中，流量数据以 10min/条的间隔进行收集，然而在这个时间尺度下， CDR 的分布过于稀疏，不利于本文的数据分析。因此，本文对数据集进行了预处理，将以 1 小时作为时间间隔。
数据集中每个时间段的流量以 100100 个网格进行统计，即每个时间段的流量数据可以由一个 100100 的流量分布矩阵组成。
本文认为网格流量不仅与前几小时的流量分布高度相关，而且还依赖于前几天当前时刻的流量分布。
要预测某月 11 日 11 点的流量，输入的数据应该有该月 8/9/10 日 11 点的流量数据（周期性数据）和当天 8/9/10 点的流量数据（近邻性数据）
如果要预测$t$时隙的流量数据$X_t$，需要输入的数据包括两部分：近邻性数据$X_c$和周期性数据$X_d$，
$$\begin{gathered} X_c=[X_{t?c},X_{t?c+1},...,X_{t?1}] \\ {X}_d=[X_{t?d?24},X_{t?(c?1)?24},...,X_{t?24}] \end{gathered}$$

2、结果

对比的模型是HA、ARIMA、LSTM、和提出的HSTCNN

对其中的一个网格的CDR进行预测

结果分析：

• HA 只是简单地从历史数据中计算出来的，缺乏对数据深层相关性的挖掘，带来较大的预测误差。
• ARIMA 只考虑数据的本身的自相关性，而不考虑其他依赖关系。
• LSTM 的性能优于统计方法，但未考虑到流量数据的时空变化，因此预测结果的表现不如 HSTCNN。
• HSTCNN 模型不仅更好地提取了流量数据的空间相关性，而且考虑了时间属性对流量变化的影响，因此得到了相对较好的性能

RMSE和R2

结果分析：
其中 HA， ARIMA， LSTM， HSTCNN 的 RMSE 分别 752， 501， 387，309；它们的 R2分别为 0.905， 0.958， 0.974， 0.984。可以看出，相比于其他三种预测模型，HSTCNN 可以获得更小的 RMSE 以及跟接近于 1 的 R2。

近邻数据和周期数据对RMSE的影响

周期数据取3（三天前的同时间数据），近邻数据对RMSE的影响是由小变大的
近邻数据取3，周期数据对RMSE的影响是由小变大的，说明小范围的周期性数据通常更有影响力，而长时间的周期难以建模，会带来较大的误差

（3）基于流量预测的动态信道分配部分

1、网络模型

UDN覆盖范围$L$，分割为多个网格，网格的尺寸由研究问题的准确性要求和复杂度决定。如果网格过小，会导致信道分配过程中计算复杂度过大。在用户关联时要以整个网格为单位， 如果网格过大，当基站数目变化时，关联结果会产生较大的误差，会对所研究问题的产生影响。
假设每个网格下所有真实用户产生的数据量或负载归类为由一个虚拟用户产生，并且假设该虚拟用户处于网格中心
基站集 B = { B S 1 , B S 2 , . . . , B S L } B=\{BS_1,BS_2,...,BS_L\} B={BS1?,BS2?,...,BSL?}
虚拟用户集 U = { U E 1 , U E 2 , . . . , U E N } U=\{UE_1,UE_2,...,UE_N\} U={UE1?,UE2?,...,UEN?}
关联矩阵：本文采用基于最近距离或最大接收功率的关联方法

2、信道分配模型

假设小基站具有相同的发射功率，相邻基站之间使用正交的信道，在互不相邻的弱干扰基站之间可以进行信道复用
下行信道资源 W = { w 1 , w 2 , . . . , w M } W=\{w_1,w_2,...,w_M\} W={w1?,w2?,...,wM?}
每个正交子信道可以分配给若干互不相邻的基站使用，每个基站也可以占用多个正交子信道。
由于每个基站下的负载不同，各子信道大小可能会不同，基站最终获得的子信道的数量和带宽也将不同。

如何确定基站与子信道的占用关系：
基站是否占用信道的矩阵：

将每个基站下的经过预测得到的负载作为信道分配的依据，负载大小决定这些基站未来分得的信道的大小。

（4）、改进方向

在流量预测过程中，本文针对性地采取了米兰市的流量数据较强的某一区域进行验
证。在数据强度较弱的区域，该方案是否也能够有较好的表现尚未可知。为了验证该方案的普适性，未来可以将研究对象从某一局部扩大到整个区域。
资源分配还应该加入功率分配
考虑到了系统吞吐量和每个用户的 QoS 水平，未来可以从能效、系统公平性等多个方面考虑

基于机器学习的无线网络负载优化方法研究_2020_徐越_北京邮电大学_博士

1、选题意义

为了后续写论文，看看：

提出个我没接触过的概念：单节点、多节点
单节点机器学习： 只有一个中心设备进行单智能体决策（集中学习？）
多节点机器学习： 原问题拆解为子问题，多个分布式计算单元分别解决（分布学习），多智能体强化学习

2、基于单节点机器学习的负载优化

（1）研究内容

两种方案

• 先预测流量，然后根据流量数据进行基站休眠，实现负载自适应的基站休眠
• 集预测和调优与一体：深度强化学习

（2）数据集分析

数据集不是公开的，是国内某运营商位于南方区域3000个4G基站的数据。数据的特征：周期化变化（工作日和周末）、白天和晚上、非周期性的随机变化
因为没有5G数据，解释一下为什么4G数据的特征也能用于5G：
文献指出，4G的周期性变化由用户的潮汐效应（用户周期性移动与人类行为的整体趋向性）引起，4G的特征在3G和C-RAN流量数据中也会被观测到，因为人的行为特性没有改变，推测5G的流量变化也不会改变。但是和3G比，4G的流量数据展现了更大尺度的非周期话，预示着5G的非周期行变化尺度可能比4G更大。

（3）基于高斯过程的无线流量预测模型

高斯过程模型的优势

将领域、专家只是融合到核函数的设计中，基于贝叶斯定理来优化模型超参数，增强模型的可解释性！！！而且高斯过程模型不仅可以预测未来的流量，还可以给出预测结果的可解释性，度量预测结果的不确定性。高斯过程模型是通过最大化模型参数的边缘概率来选择最佳的模型参数，即使数据集规模有限，高斯过程模型也能避免过拟合问题，很适合在无线（用户端）收集数据代价高的问题

what？

和数学的高斯分布不同，机器学习领域的高斯过程模型是一种核方法，用来解决“回归问题”。最常见的回归模型就是线性回归，是一种使用参数的函数拟合数据分布的方法。但是高斯过程模型是非参数模型，使用核函数刻画数据点之间的相关性，通过优化核函数的超参数来逼近最优解。

how？

具体的我有点看不懂，写一写我看得懂的。（后续如果我的工作有需要的话可以在加深理解😰）
使用4G的流量特性（领域知识）作为核函数，然后线性组合。

• 星期周期性
• 天周期性
• 非周期性
  对于5G流量，非周期性更强，增加一个有理二次核函数。

训练模型超参数

主流方法：最大化高斯过程的边缘似然函数
梯度下降法

（4）基于深度强化学习的负载均衡模型

移动性负载均衡技术：将通过控制用户切换把过载小区的负载合理的转移到相邻的小区中，实现负载均衡，提高资源利用效率。
CIO:cell individual offset小区偏置量

用户切换

用户吞吐量

基站负载

假设每个用户在$t$时刻都有常数比特通讯需求CBR

负载均衡问题建模（强化学习）

状态：基站的负载分布和用户分布

直接使用负载分布和用户分布作为状态输入模型会出现问题：

• 状态空间过大，无法枚举
• 高位数据计算复杂度高，传输时延较大
• 原始数据包含冗余信息，影响学习性能
  solution：使用高阶的特征来表示无线系统的状态作为模型输入
  负载分布：每个基站的负载相对于所有基站的负载的偏移量
  用户分布：每个基站边缘用户的比例（用户在当前基站的接收信噪比和连接相邻基站的接收信噪比来判断是否为边缘用户）
  

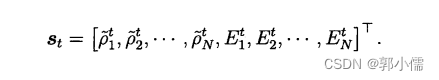
动作：CIO调整

每个基站的COI，考虑的COI是连续变量

收益：负载均衡指标

最小化最大的基站的负载值（最坏情况）
最大化最大的基站负载值的倒数

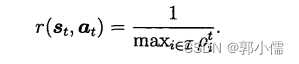
后续采用的DDPG算法

（5）仿真结果

对比高斯过程模型：

• SARIMA：容易受突发流量影响
• SS：误差稳定但较高
• LSTM和RNN：过拟合和欠拟合

流量预测模型用于优化基站休眠：

在保证用户QoS的前提下提升系统的节能效率
目标函数：
使用权重就能权衡QoS和能耗
由于基站流量的不确定性，在进行基站休眠时，要为相邻的基站预留资源，降低因为流量波动导致的网络过载的概率，所以如果没有对流量的预测，一般会根据历史的最高流量负载来设定基站的预留资源，这样对资源造成极大地浪费。但是当有了流量预测之后，相邻基站可以合理的设定自己的资源预留值
四种休眠方式：

• 基于未来的真实流量来控制基站休眠（性能上限）
• 基于当前的真实流量来控制基站休眠
• 基于高斯过程预测未来流量来控制基站休眠
• 不进行基站休眠