机器学习（六） — 评估模型

Evaluate model

1 test set

1. split the training set into training set and a test set
2. the test set is used to evaluate the model

1. linear regression

compute test error

$$J_{test}(\vec{w},b)=\frac{1}{2m_{test}}\sum _{i=1}^{m_{test}}\left[(f(x_{test}^{(i)})?y_{test}^{(i)}{)}^2\right]$$

2. classification regression

compute test error

$$J_{test}(\vec{w},b)=?\frac{1}{m_{test}}\sum _{i=1}^{m_{test}}\left[y_{test}^{(i)}log(f(x_{test}^{(i)}))+(1?y_{test}^{(i)})log(1?f(x_{test}^{(i)})\right]$$

2 cross-validation set

1. split the training set into training set, cross-validation set and test set
2. the cross-validation set is used to automatically choose the better model, and the test set is used to evaluate the model that chosed

3 bias and variance

1. high bias: $J_{train}$ and $J_{cv}$ is both high
2. high variance: $J_{train}$ is low, but $J_{cv}$ is high

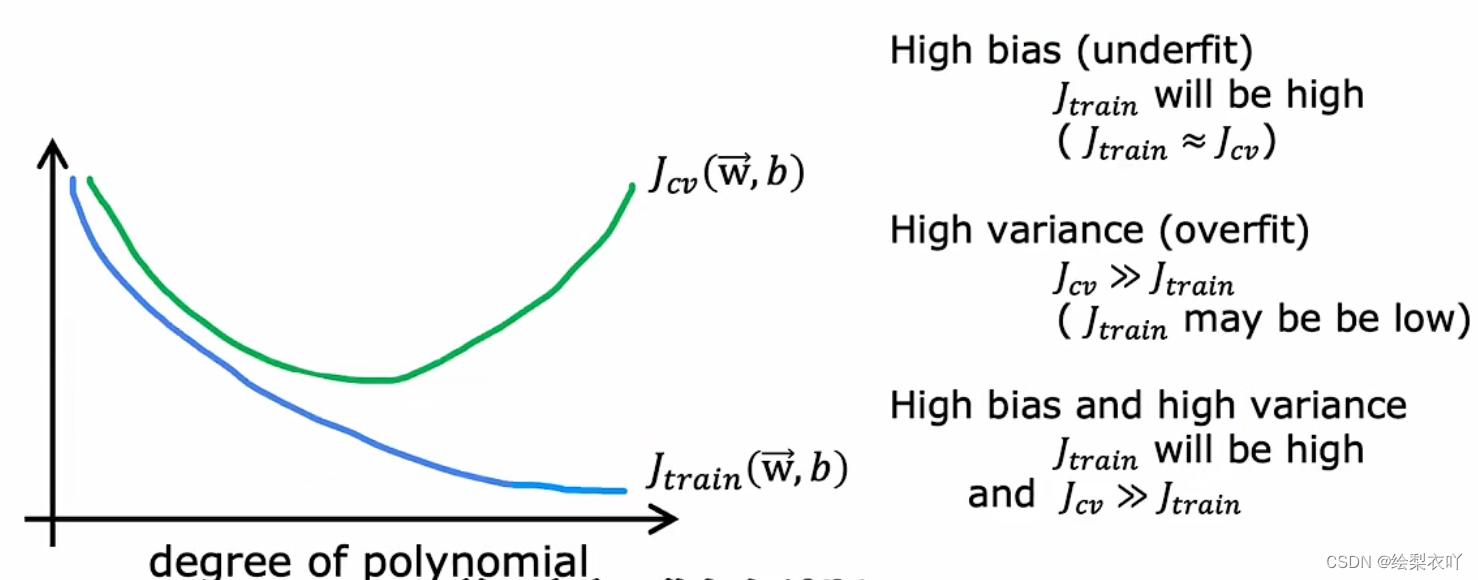
3. if high bias: get more training set is helpless
4. if high variance: get more training set is helpful

4 regularization

1. if $\lambda$ is too small, it will lead to overfitting(high variance)
2. if $\lambda$ is too large, it will lead to underfitting(high bias)

5 method

1. fix high variance:
   • get more training set
   • try smaller set of features
   • reduce some of the higher-order terms
   • increase $\lambda$
2. fix high bias:
   • get more addtional features
   • add polynomial features
   • decrease $\lambda$

6 neural network and bias variance

1. a bigger network means a more complex model, so it will solve the high bias
2. more data is helpful to solve high variance

3. it turns out that a bigger(may be overfitting) and well regularized neural network is better than a small neural network