理解排序算法：冒泡排序、选择排序与归并排序

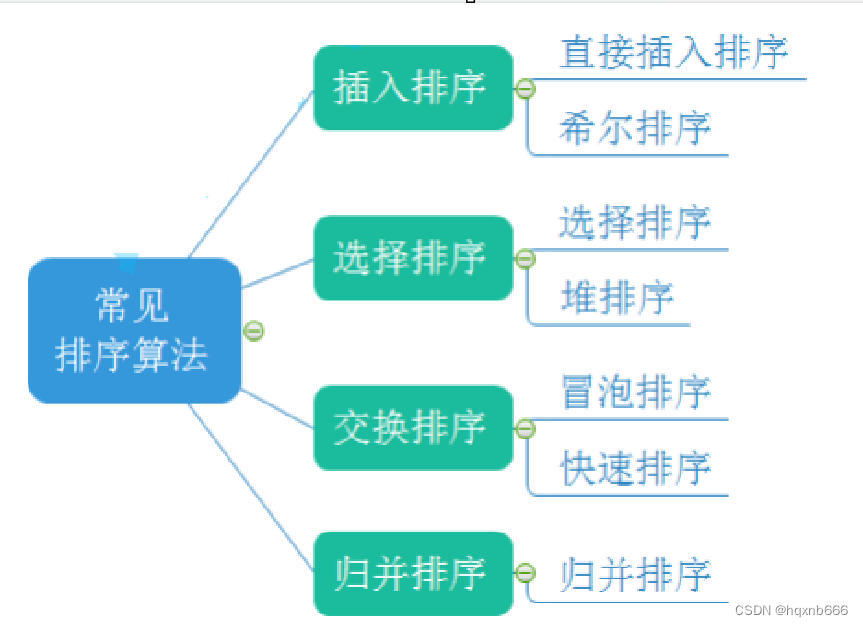
简介： 在计算机科学中，排序算法是基础且重要的概念。本文将介绍三种常见的排序方法：冒泡排序、选择排序和归并排序。我们将探讨它们的工作原理、特点和适用场景，以帮助读者更好地理解和选择合适的排序方法。

冒泡排序?

冒泡排序是一种简单的排序算法。它通过重复地遍历要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。这个过程重复进行，直到没有再需要交换的元素，此时数列已经排序完成。冒泡排序的特点是实现简单，但效率较低，特别是在处理大数据集时。

?

?

void BubbleSort(int* a, int n)//使用bool来进阶冒泡 ，当有一层不交换，就代表已经排完序，防止永久时间复杂度都是O(n^2)
{
	for (int j = 0; j < n; j++)
	{
		bool exange = false;
		for (int i = 1; i < n - j; i++)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exange = true;
			}
		}
		if (exange == false)
			break;
	}

}

?冒泡排序的特性总结：

1. 冒泡排序是一种非常容易理解的排序

2. 时间复杂度：O(N^2)

3. 空间复杂度：O(1)

4. 稳定性：稳定

选择排序

?

选择排序是一种简单直观的排序算法，广泛应用于计算机科学教学和一些基础编程任务中。本文将详细介绍选择排序的工作原理、具体实现步骤、算法特点以及适用场景，帮助读者更好地理解和使用这种排序方法。

一、选择排序的工作原理

选择排序算法的基本思想是：

首先在未排序的序列中找到最小（或最大）的元素，然后将其放置在序列的起始位置，接着再从剩余未排序的元素中继续寻找最小（或最大）的元素，然后放到已排序序列的末尾。这个过程一直重复，直到所有元素都被排序。

二、选择排序的步骤

1. 从未排序的序列中找到最小（或最大）的元素。
2. 将找到的最小（或最大）元素与序列的第一个元素交换位置（如果最小元素就是第一个元素，则自身和自身交换）。
3. 重复上述过程，每次交换后，排序序列的长度就增加一个元素，而未排序序列的长度减少一个元素。
4. 当未排序序列的长度减少到0时，排序就完成了。

三、选择排序的特点

• 简单直观：选择排序的算法逻辑简单，易于理解和实现。
• 时间复杂度：在最好、最坏和平均情况下，时间复杂度都是O(n2)。
• 不稳定排序：选择排序不是稳定的排序算法，相等的元素可能在排序过程中改变其原有的顺序。
• 原地排序：选择排序不需要额外的存储空间，它是一种原地排序算法。

四、选择排序的适用场景

由于选择排序的效率较低，它通常不适用于数据量较大的排序任务。然而，在数据量较小或者对算法的时间复杂度要求不高的场景中，选择排序由于其实现的简单性，仍然是一个不错的选择。特别是在教学和学习算法的过程中，选择排序是理解基本排序概念的良好起点。

总结： 选择排序以其简单直观的特点，在编程教学和小规模数据处理中有着一席之地。虽然在处理大量数据时效率不高，但它作为基础排序算法，对于理解更复杂的排序技术提供了重要的基础。

void SelectSort(int* a, int n)
{
	int begin = 0;
	int end = n - 1;
	while (begin < end)
	{
		int mini = begin; 
		int max = begin;
		for (int i = begin+1; i <= end; ++i)
		{
			if (a[i] < a[mini])
			{
				mini = i;
			}
			if (a[i] > a[max])
			{
				max = i;
			}
		}
		Swap(&a[begin], &a[mini]);
		if (max == begin)
		{
			max = mini;
		}
		Swap(&a[end], &a[max]);
		begin++;
		end--;
	}
	
}

?归并排序

?

?

简介： 归并排序是一种高效且稳定的排序算法，通过分治法实现对数据的高效排序。本文旨在详细介绍归并排序的工作原理、具体实现步骤、算法的特点以及适用场景，帮助读者深入理解并有效地应用这种排序方法。

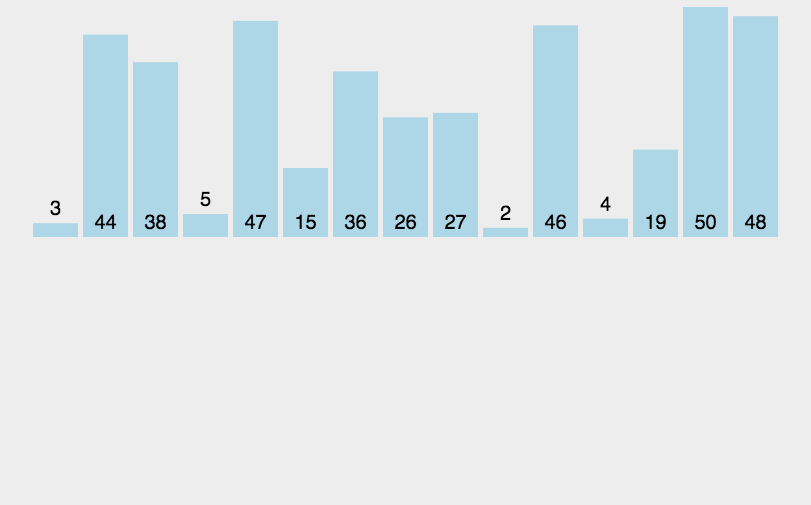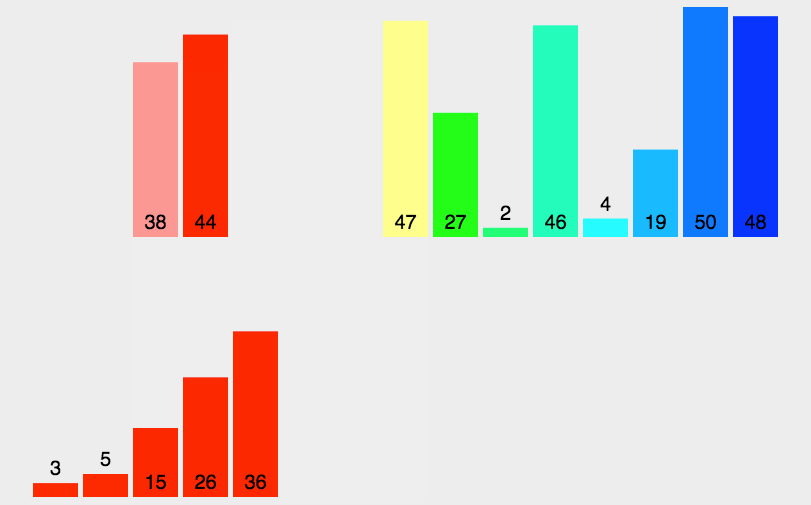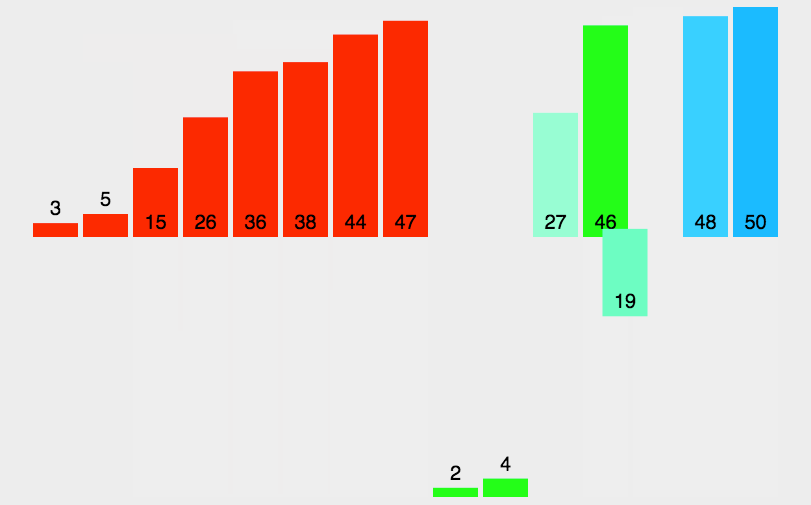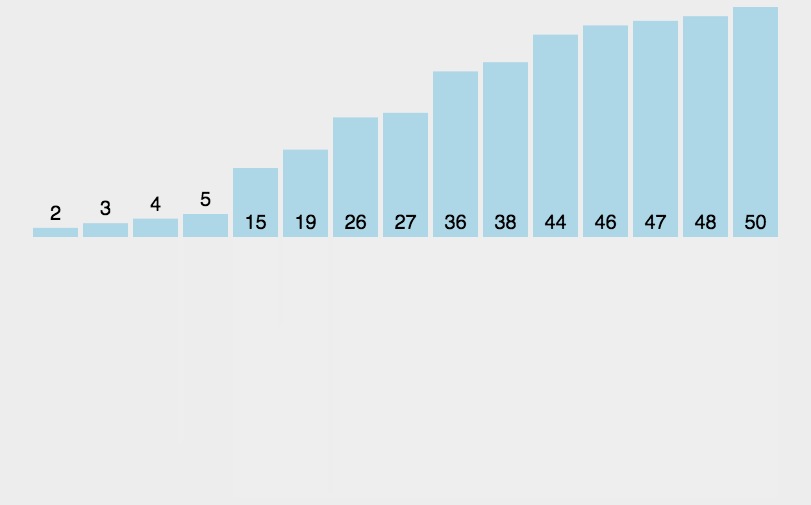
一、归并排序的工作原理

归并排序的核心思想是将两个有序的数组合并成一个更大的有序数组。具体来说，它将原始数组分成两半，分别对这两半进行排序，然后将排序好的两个半部分合并在一起。这个过程是递归进行的，最终达到完全排序的目的。

二、归并排序的步骤

1. 分解：将原始数组分解成两个大小大致相等的子数组。
2. 解决：递归地对这两个子数组进行归并排序。
3. 合并：将两个已排序的子数组合并成一个单一的已排序数组。

三、归并排序的特点

• 高效稳定：归并排序在最坏、最好和平均情况下的时间复杂度均为O(n log n)，是一种非常高效的排序算法。同时，它也是一种稳定的排序，即相等的元素在排序后会保持其原有顺序。
• 分治策略：归并排序是分治法思想的典型应用，通过将问题分解为可管理的子问题来简化复杂性。
• 额外空间需求：归并排序需要额外的空间来存储临时数组，这是它的一个缺点。

四、归并排序的适用场景

归并排序非常适合处理大数据集，特别是在数据无法一次性装入内存时。由于其稳定性和高效性，它广泛应用于数据库和文件系统等领域，是处理大规模数据排序的理想选择。

总结： 归并排序以其高效、稳定的特性，在大数据处理和复杂系统中占有重要位置。尽管需要额外的存储空间，但其优越的性能使其成为解决复杂排序问题的强大工具。

void _MergeSort(int* a, int begin, int end, int* tmp)//每次需要开辟数组且要对数组进行分区，所以调用子函数
{
	int mid = (begin + end) / 2;
	//[begin , mid] [mid +1, end]
	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid + 1, end, tmp);
	//后序逻辑 归并
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin;
	
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}
		while (begin1 <= end1)
		{
			tmp[i++] = a[begin1++];
		}
		while (begin2 <= end2)
		{
			tmp[i++] = a[begin2++];
		}

		memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));

}
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
		return;
	}
	_MergeSort(a, 0, n - 1, tmp);
	free(tmp);
}

?

总结： 在本系列博客文章中，我们深入探讨了三种经典的排序算法：冒泡排序、选择排序和归并排序。每种排序方法都有其独特的工作原理和应用场景，从简单直观的冒泡排序和选择排序到高效稳定的归并排序，这些算法为我们提供了不同的数据组织和处理方式。

冒泡排序以其实现的简单性和直观性而闻名，适合用于小数据集和教学目的。选择排序，尽管时间复杂度较高，但在需要减少交换次数的情况下仍是一个不错的选择。归并排序则以其高效率和稳定性在大数据处理中发挥重要作用，尤其适用于无法一次性装入内存的大规模数据集。

理解这些排序算法的原理和特点对于任何涉及数据处理的程序员来说都是至关重要的。它们不仅是计算机科学的基础，也是解决实际问题的强大工具。我们希望这些文章能够帮助读者更好地理解这些基本算法，并在适当的场合中作出恰当的选择。

感谢您阅读本系列关于排序算法的探索。我们期待在未来的文章中继续为您提供更多有价值的技术洞见和实用建议。