多层感知机

目录

一、感知机

1、相关概念介绍

2、（单层）感知机存在的问题

3、总结

二、多层感知机（MLP）

1、多层感知机思路

2、激活函数

3、常见的激活函数

4、多类分类

4、总结

三、多层感知机从零开始实现

1、读取数据集

2、初始化模型参数

3、激活函数

4、定义模型

5、定义损失函数

6、定义优化算法

7、训练

四、多层感知机的简洁实现

1、定义模型并初始化模型参数

2、定义损失函数和优化算法

3、读取数据集并训练

---

一、感知机

1、相关概念介绍

???????感知机（perceptron）是二分类的线性分类模型，属于监督学习算法。输入为实例的特征向量，输出为实例的类别（取+1和-1）。

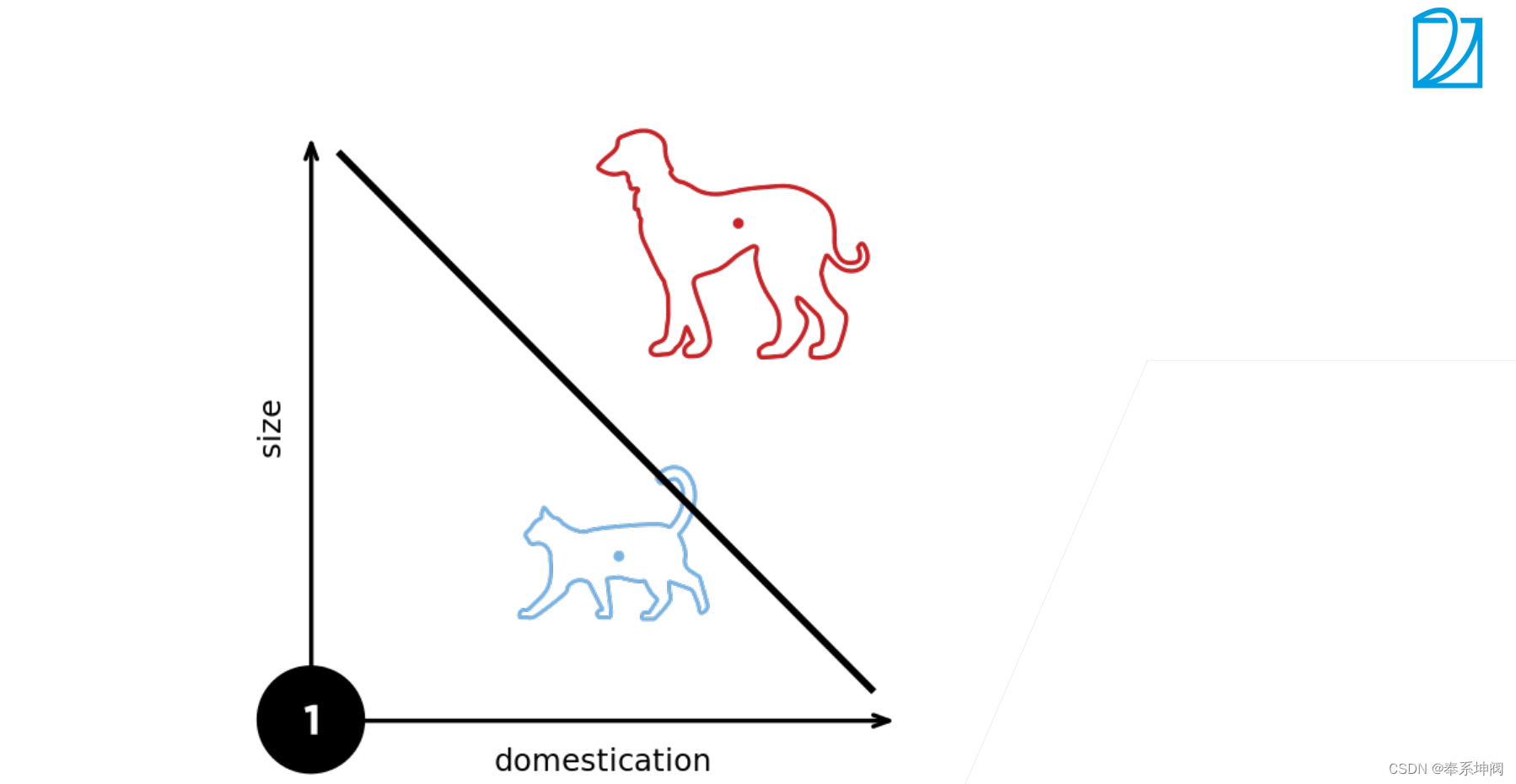
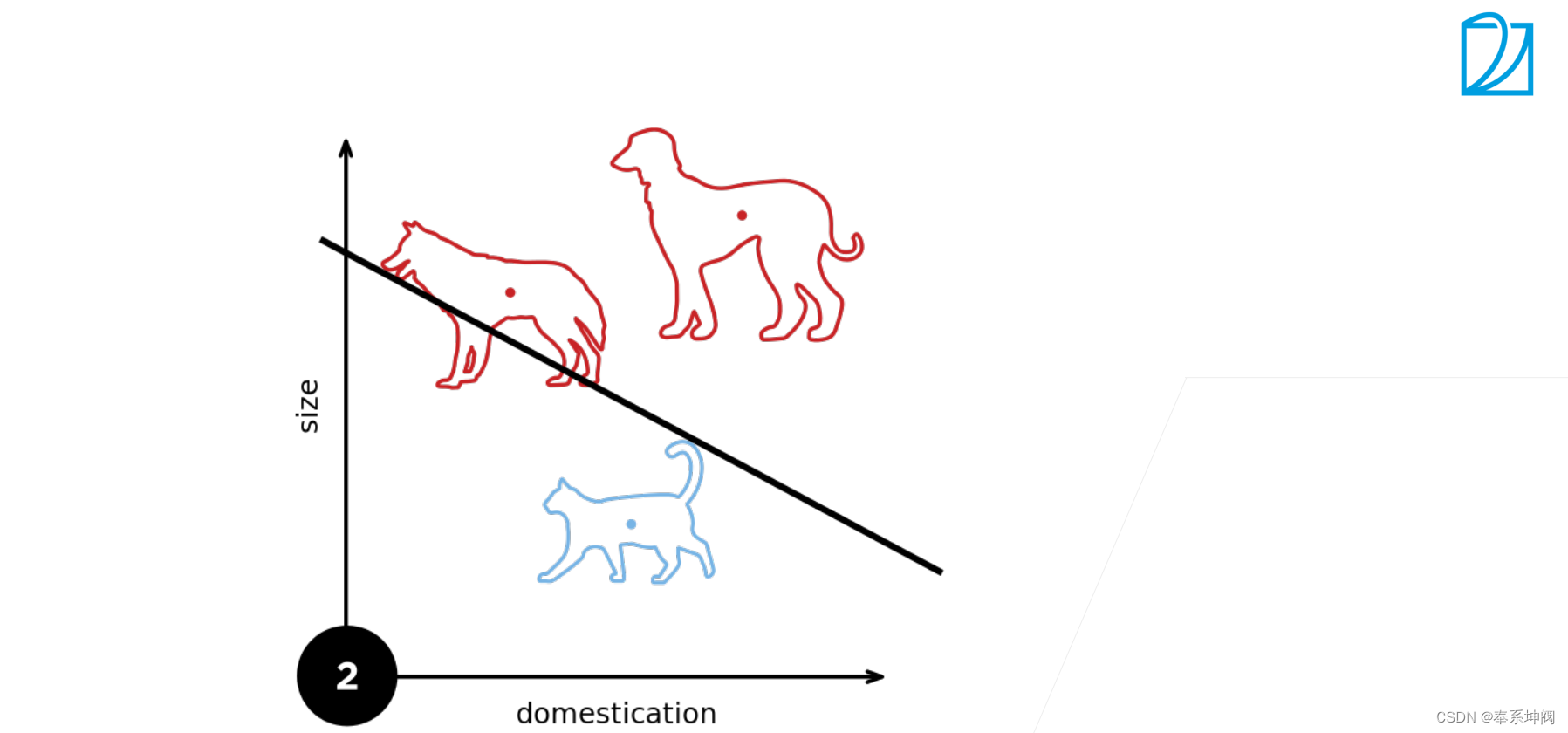
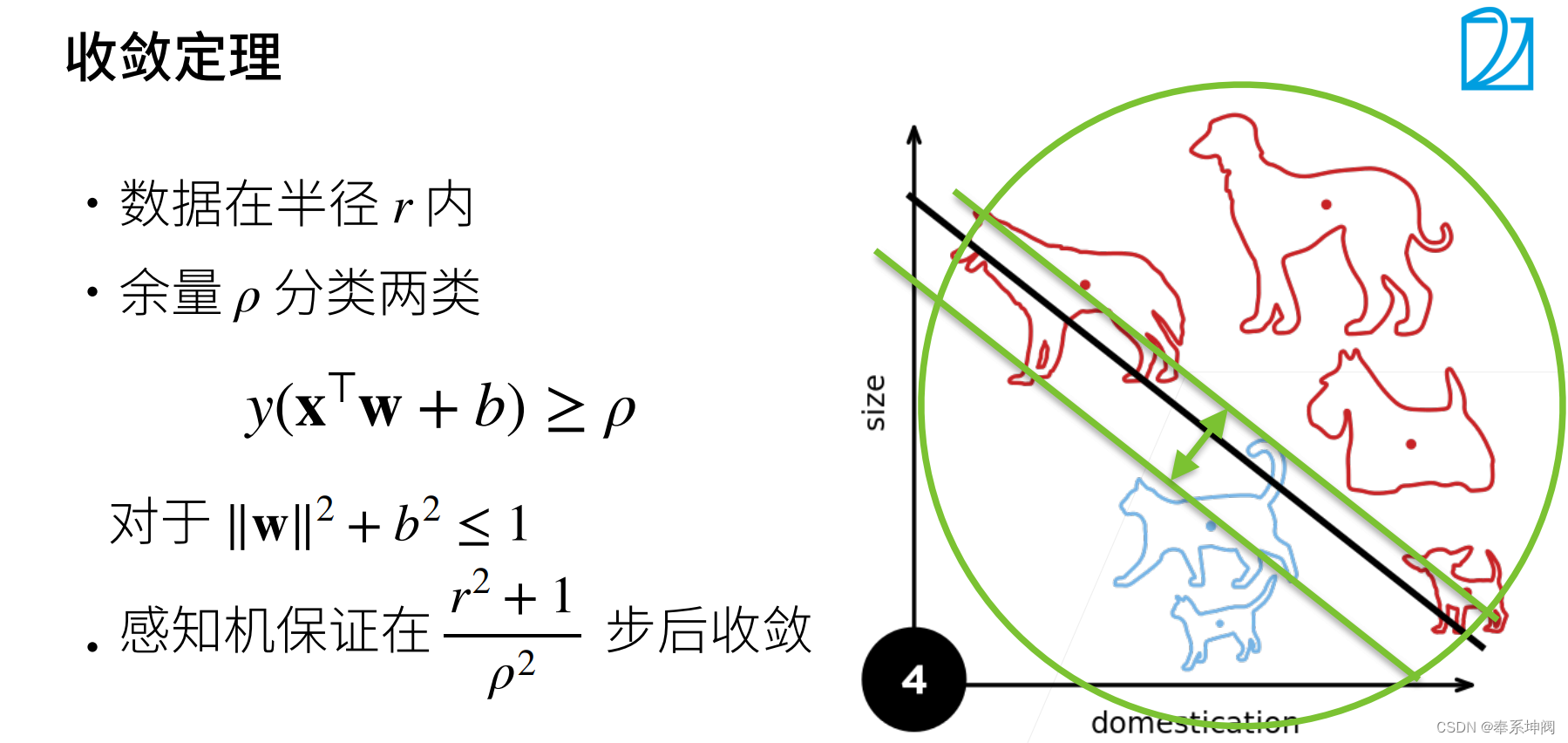
2、（单层）感知机存在的问题

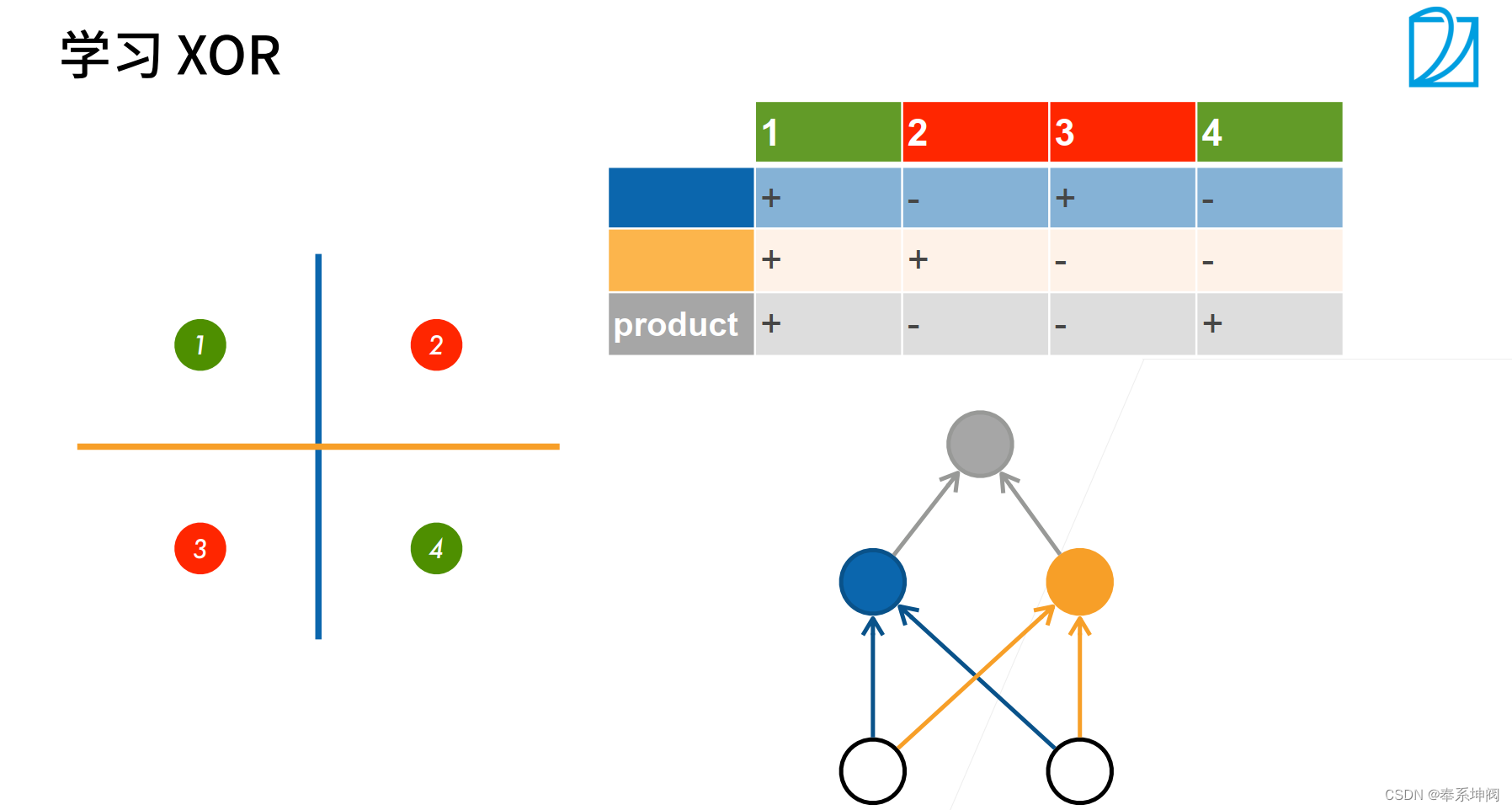
???????感知机不能拟合XOR函数，它只能产生线性分割面。

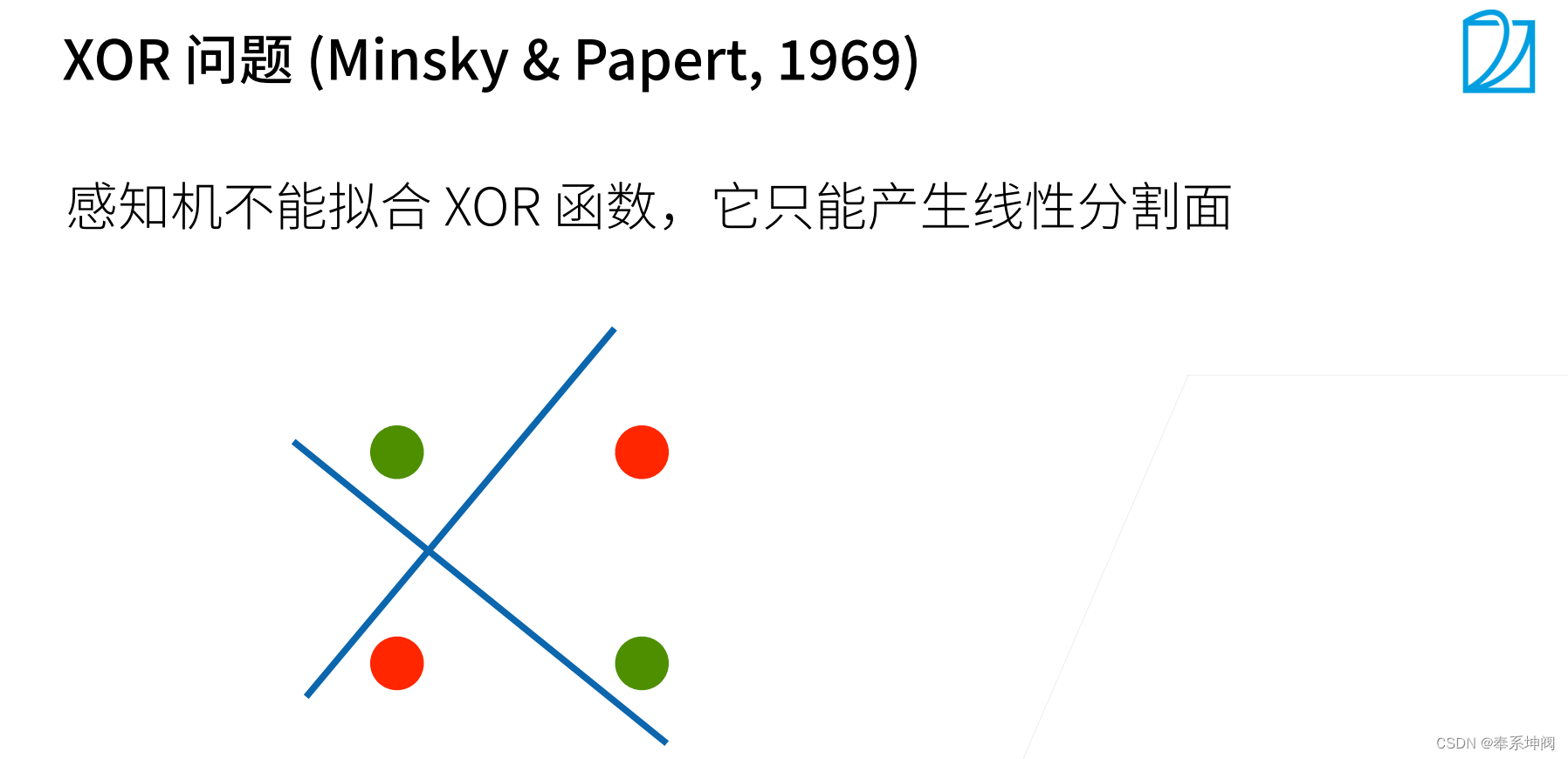
3、总结

二、多层感知机（MLP）

1、多层感知机思路

???????多层感知机思路就是将一次不能完成学习的东西分多次进行学习。针对XOR问题就是先学一个x，再学一个y，然后再将这两次学习的结果组合起来。

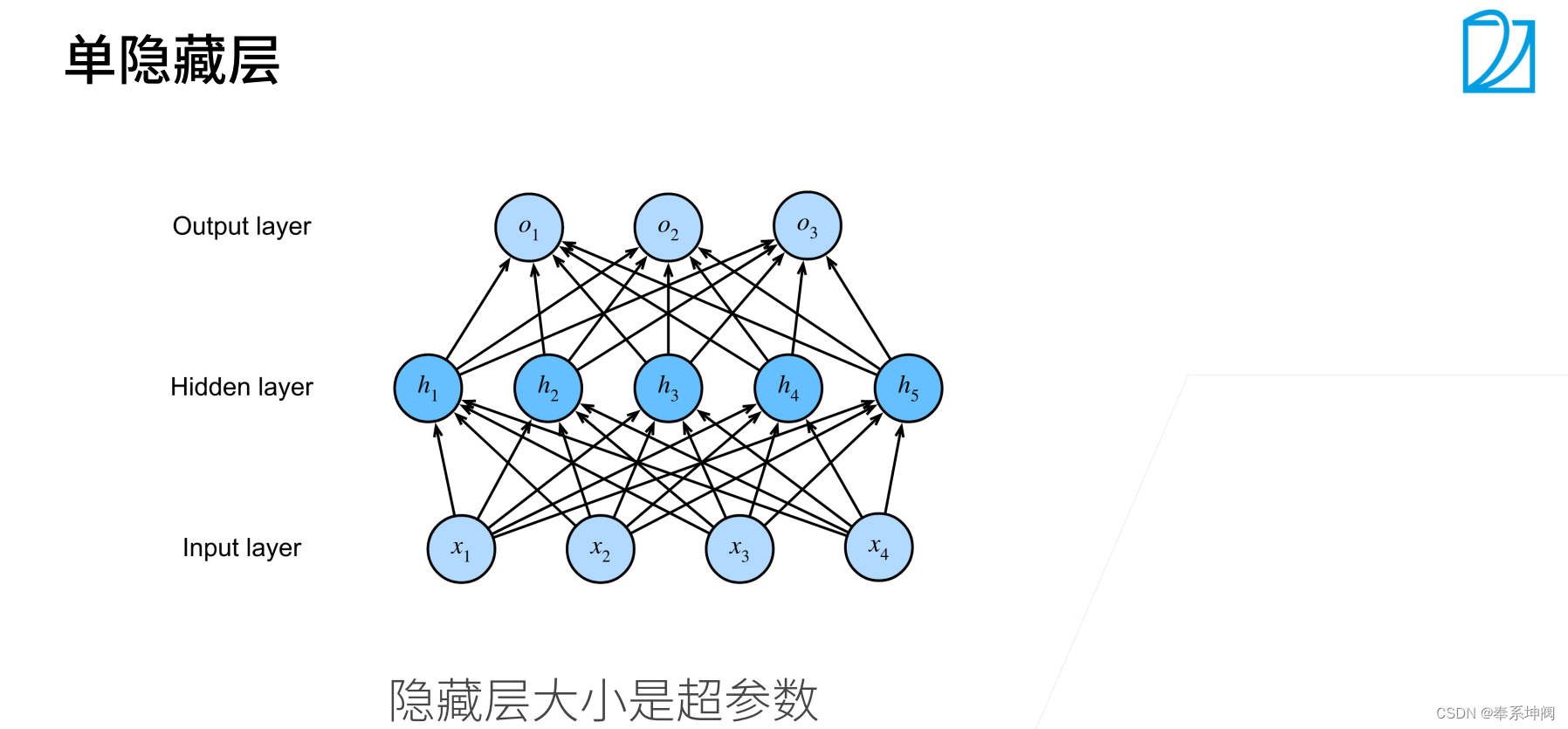
2、激活函数

???????激活函数不能是线性的，一定要使用非线性的激活函数，否则会造成模型坍塌。

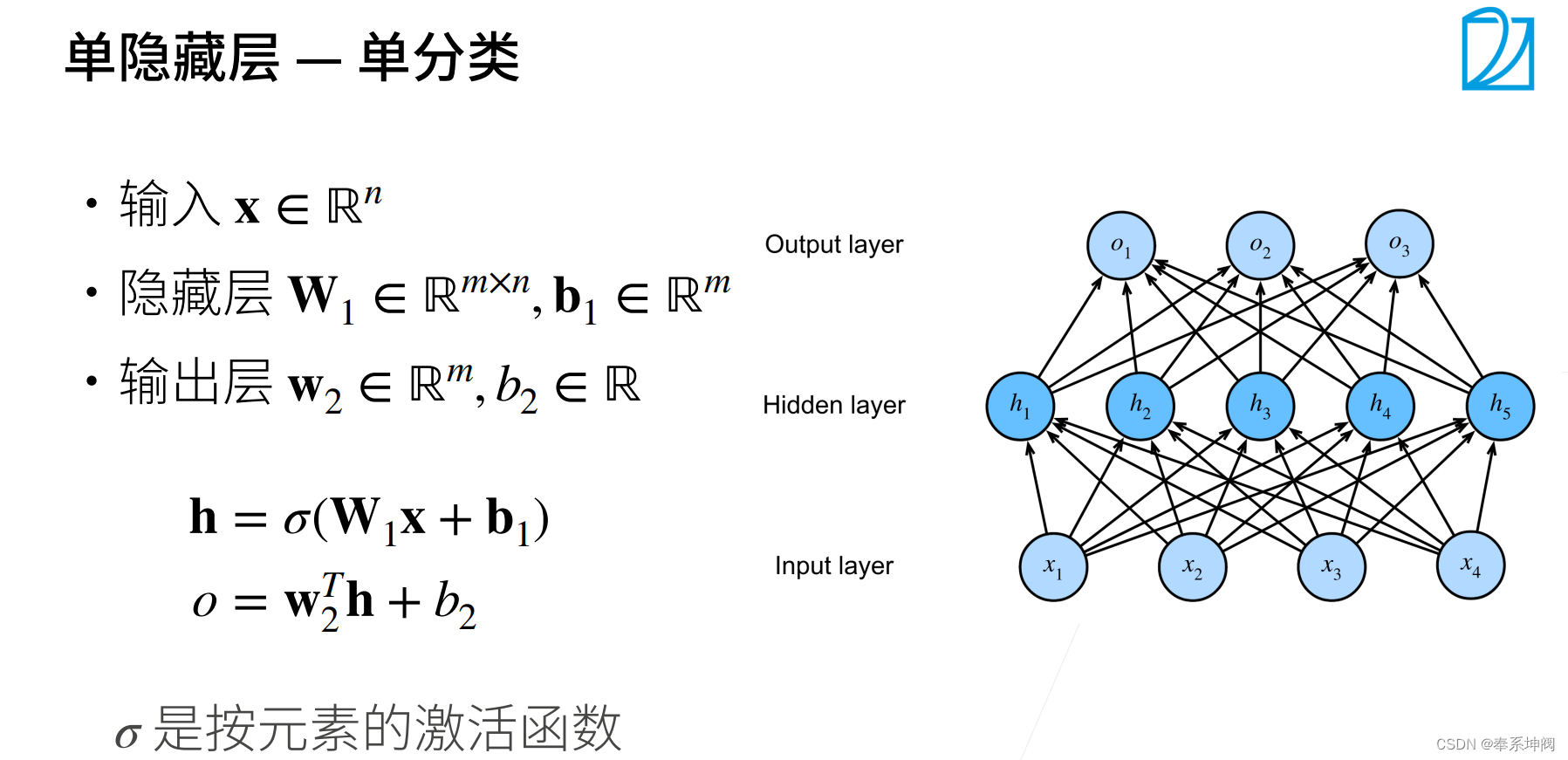
例如，如果激活函数为：

那么输出仍然是线性函数，其实仍然相当于一个单层的感知机

3、常见的激活函数

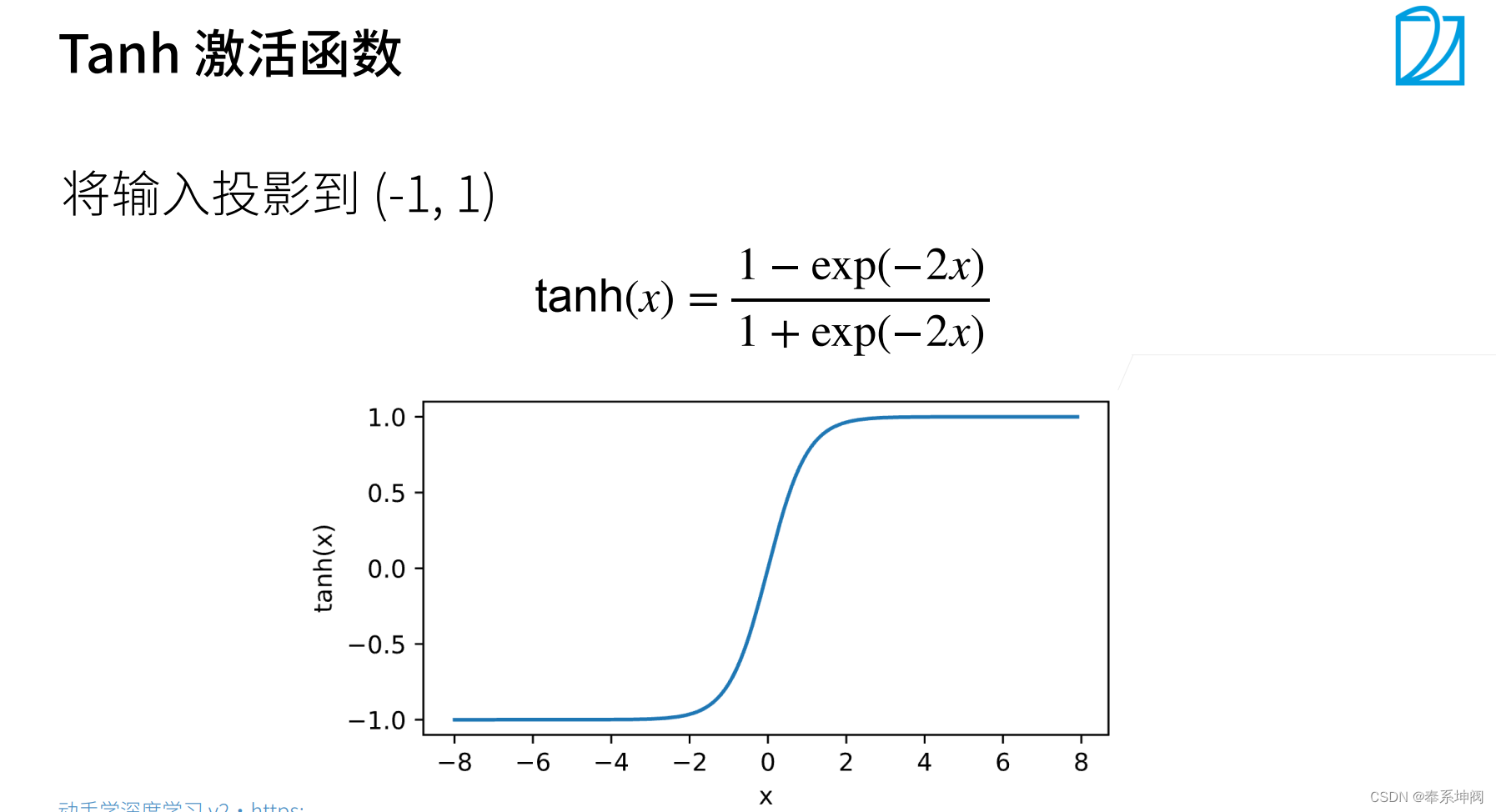
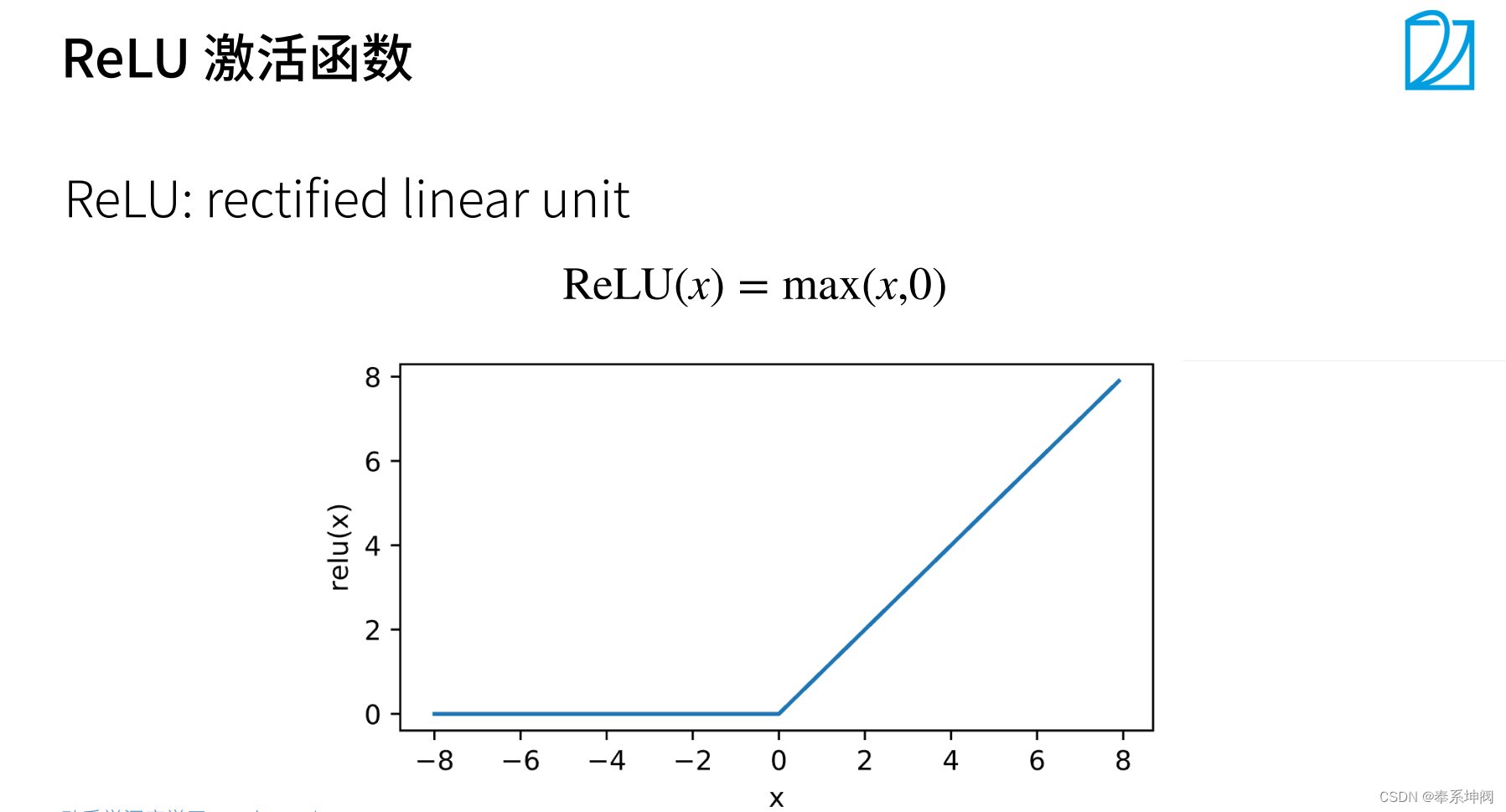
???????ReLU函数是其中最常用的函数，因为其计算起来很快，相比于Sigmoid函数和Tanh函数来讲没有指数运算。因为指数运算较慢，因此有时候使用ReLU激活函数节约算力。

4、多类分类

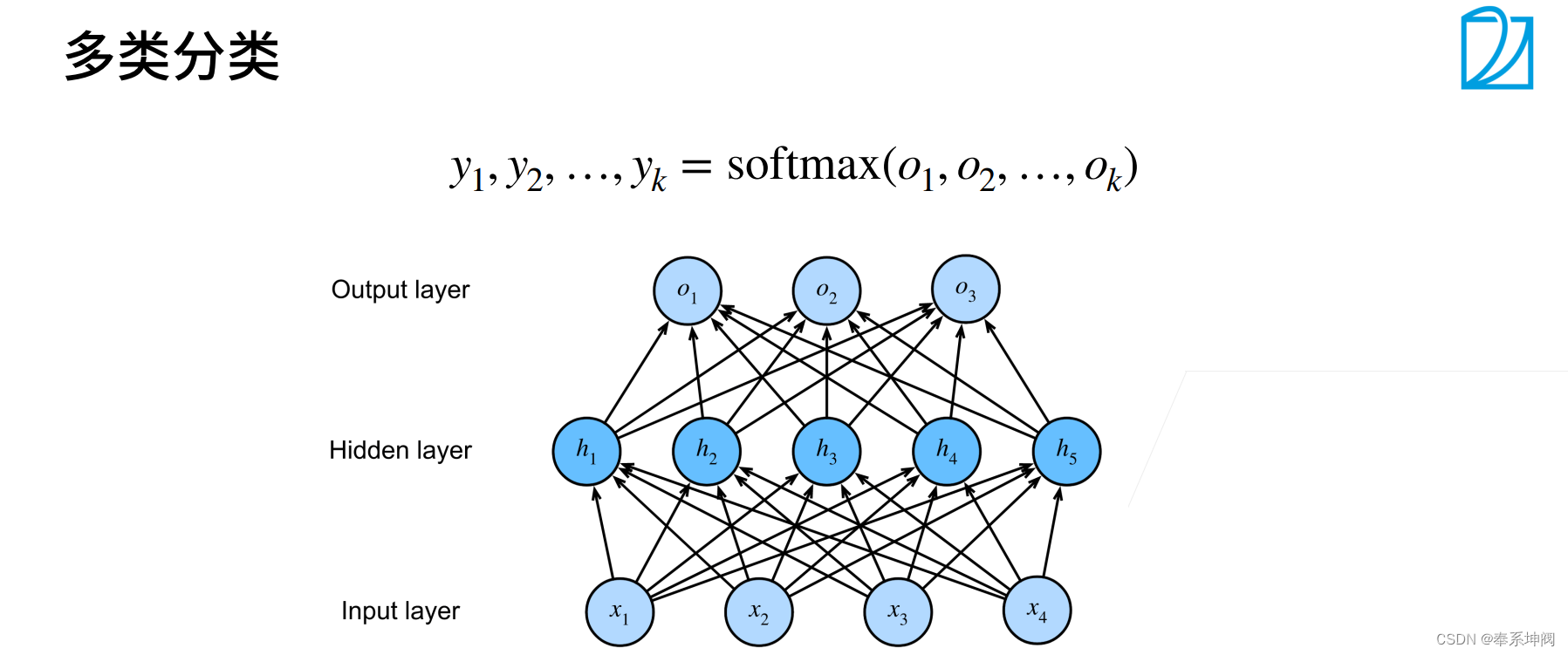
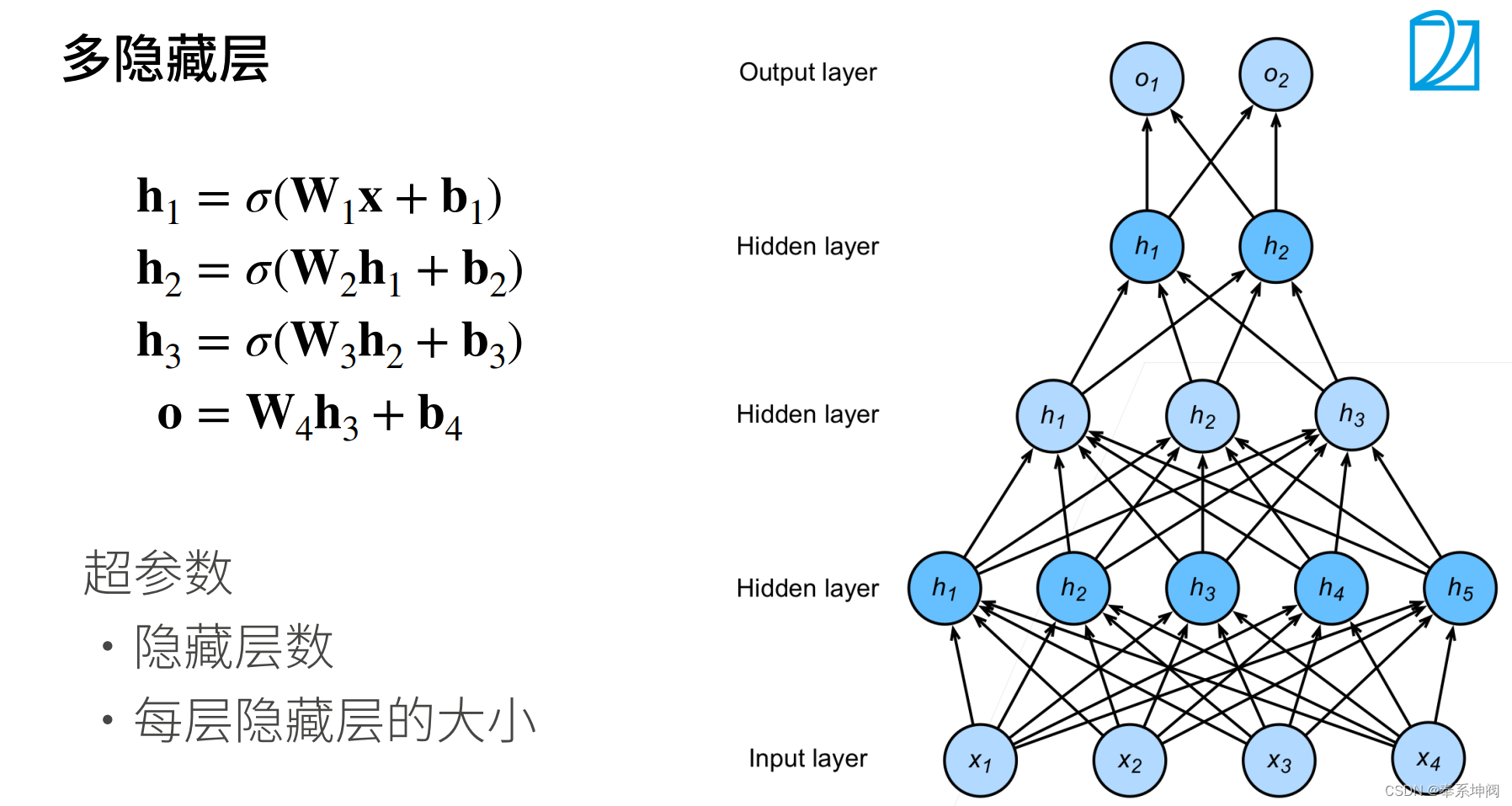
4、总结

三、多层感知机从零开始实现

???????我们已经在前面中描述了多层感知机（MLP），现在让我们尝试自己实现一个多层感知机。为了与之前softmax回归（Softmax回归-CSDN博客）获得的结果进行比较，我们将继续使用Fashion-MNIST图像分类数据集。

import torch
from torch import nn
from d2l import torch as d2l

1、读取数据集

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

2、初始化模型参数

???????回想一下，Fashion-MNIST中的每个图像由个灰度像素值组成。所有图像共分为10个类别。忽略像素之间的空间结构，我们可以将每个图像视为具有784个输入特征和10个类的简单分类数据集。首先，我们将实现一个具有单隐藏层的多层感知机，它包含256个隐藏单元。注意，我们可以将这两个变量都视为超参数。通常，我们选择2的若干次幂作为层的宽度。因为内存在硬件中的分配和寻址方式，这么做往往可以在计算上更高效。

???????我们用几个张量来表示我们的参数。注意，对于每一层我们都要记录一个权重矩阵和一个偏置向量。跟以前一样，我们要为损失关于这些参数的梯度分配内存。

num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01)    # nn.Parameter()加不加都行，主要作用是声明是torch的Parameter
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

3、激活函数

???????为了确保我们对模型的细节了如指掌，我们将自己动手实现ReLU激活函数，而不是直接调用内置的`relu`函数。

def relu(X):
    a = torch.zeros_like(X)
    return torch.max(X, a)

4、定义模型

???????因为我们忽略了空间结构，所以我们使用`reshape`将每个二维图像转换为一个长度为`num_inputs`的向量。只需几行代码就可以实现我们的模型。

def net(X):
    X = X.reshape((-1, num_inputs))     # num_inputs:784  -1：batch_size
    H = relu(X @ W1 + b1)  # 这里“@”代表矩阵乘法
    return (H @ W2 + b2)

5、定义损失函数

???????由于我们已经从零实现过softmax函数，因此在这里我们直接使用高级API中的内置函数来计算softmax和交叉熵损失。

loss = nn.CrossEntropyLoss(reduction='none')    # 里面内置softmax和交叉熵损失算法

6、定义优化算法

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)

7、训练

d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

四、多层感知机的简洁实现

???????下面将介绍通过高级API更简洁地实现多层感知机。

import torch
from torch import nn
from d2l import torch as d2l

1、定义模型并初始化模型参数

???????与softmax回归的简洁实现相比，唯一的区别是我们添加了2个全连接层（之前我们只添加了1个全连接层）。第一层是隐藏层，它包含256个隐藏单元，并使用了ReLU激活函数。第二层是输出层。

net = nn.Sequential(nn.Flatten(),
                    nn.Linear(784, 256),
                    nn.ReLU(),
                    nn.Linear(256, 10))

def init_weights(m):    # 初始化模型参数
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights)

2、定义损失函数和优化算法

batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)

3、读取数据集并训练

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)