LeetCode 84：柱状图中的最大矩形

一、题目描述

给定?n?个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

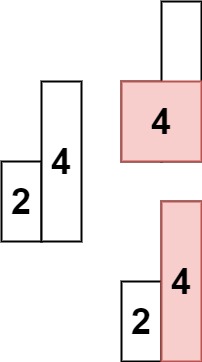
输入： heights = [2,4]
输出： 4

提示：

• 1 <= heights.length <=105
• 0 <= heights[i] <= 104

二、思路分析

使用栈空间来解决本题，通过空间换时间的方式。

三、代码参考

1、Java

class Solution {
    public int largestRectangleArea(int[] heights) {
        // 获取数组长度
        int len = heights.length;
        // 数组长度为 0 或者 1 时直接返回
        if(len == 0){
            return 0;
        }
        if(len == 1){
            return heights[0];
        }
        // 用来返回最大面积，初始值为 0
        int area = 0;
        // 创建栈空间做辅助
        Deque<Integer> stack = new ArrayDeque<>();
        // 循环遍历数组
        for(int i = 0; i < len; i++){
            // 
            while(!stack.isEmpty() && heights[stack.peekLast()] > heights[i]){
                // 获取栈顶高度，并移除当前栈顶
                int height = heights[stack.removeLast()];
                // 做特殊的处理，如果当前栈顶的高度和上一个栈顶的高度相同，则也需要进行弹栈
                while(!stack.isEmpty() && heights[stack.peekLast()] == height){
                    // 移除栈顶元素
                    stack.removeLast();
                }
                // 创建宽度变量，初始值为 0
                int width = 0;
                // 如果栈为空，说明，有效柱体能够从 i 的左边一直延伸到第一个开始
                if(stack.isEmpty()){
                    // 所以此时的宽度为 i
                    width = i;
                }else {
                    width = i - stack.peekLast() - 1;
                }
                // 计算面积, 长 * 宽，并获取最大面积
                area = Math.max(area, height * width);
            }
            // 将下标存入栈空间中
            stack.addLast(i);
        }
        // 将当前栈中的所有元素弹出
         while(!stack.isEmpty()){
                // 获取栈顶高度，并移除当前栈顶
                int height = heights[stack.removeLast()];
                // 做特殊的处理，如果当前栈顶的高度和上一个栈顶的高度相同，则也需要进行弹栈
                while(!stack.isEmpty() && heights[stack.peekLast()] == height){
                    // 移除栈顶元素
                    stack.removeLast();
                }
                // 创建宽度变量，初始值为 0
                int width = 0;
                // 如果栈为空，说明，有效柱体能够从 i 的左边一直延伸到第一个开始
                if(stack.isEmpty()){
                    // 所以此时的宽度为 len
                    width = len;
                }else {
                    width = len - stack.peekLast() - 1;
                }
                // 计算面积, 长 * 宽，并获取最大面积
                area = Math.max(area, height * width);
            }
        // 返回面积结果
        return area;
    }
}

2、Python

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        size = len(heights)
        area = 0

        stack = []

        for i in range(size):
            while len(stack) > 0 and heights[i] < heights[stack[-1]]:
                height = heights[stack.pop()]

                while len(stack) > 0 and height == heights[stack[-1]]:
                    stack.pop()

                if len(stack) > 0:
                    width = i - stack[-1] - 1
                else:
                    width = i

                area = max(area, height * width)
            stack.append(i)

        while len(stack) > 0 is not None:
            height = heights[stack.pop()]
            while len(stack) > 0 and height == heights[stack[-1]]:
                stack.pop()

            if len(stack) > 0:
                width = size - stack[-1] - 1
            else:
                width = size
            area = max(area, height * width)

        return area