后缀数组模板

详细理解后缀数组求sa数组的函数，该函数可以看为主要分为三个部分，第一个部分是预处理；第二个部分是进行基数排序，首先根据第二关键词排序，然后根据第一关键字排序；第三个部分是根据排序后的结果重新为每个字符串分配桶。后两个部分以倍增的形式重复，直到排序结束。

理解各个数组的含义

x[i]：记录原始下标为i的字符串所在桶的编号
c[i]：记录编号为i的桶，在所有桶中的累计价值，也就是前缀和，在求前缀和之前，要求编号为i的桶里所装的字符串的个数
y[i]：辅助数组，当对sa数组进行改变时，提前存一下sa数组，当对x数组进行改变时，提前存一下x数组
sa[i]：排序后下标为i的字符串在原始序列中的下标

第一部分，预处理

根据所有后缀字符串的第一个字符进行排序
第一个for循环：s表示的是原始字符串，那么对于下标为i的后缀字符串，s[i]存的就是它的第一个字符，初始时，直接按照第一个字符的值分配桶，所以有

x[i]=s[i]

，同时还要统计x[i]号桶此时存的字符串数量，所以有

c[x[i]=s[i]]++

第二个for循环：求每个桶的累计价值，也就是前缀和，所以这里i <= m，m表示的是桶的个数
第三个for循环：求sa数组，这里就是根据桶里的累计值进行排序了，求出原始下标为i的字符串所在的桶编号，即x[i]，然后求该桶在所有桶中的累计值c[x[i]]，这个就是原始下标为i的字符串此时的排序，所以有sa[c[x[i]] = i，此时相当于我们从桶中取出了一个值，那么桶的累计值要减1，所以有

sa[c[x[i]]–] = i;

for(int i = 1;i <= n;i++) c[x[i]=s[i]]++;
for(int i = 1;i <= m;i++) c[i] += c[i-1];
for(int i = n;i >= 1;i--) sa[c[x[i]]--] = i;

倍增的框架

for(int k = 1;k <= n;k = k << 1) {}	

按照第二关键字排序

每次排序前我都要重新分配桶，所以先对c数组清空。
第一个for循环：每次排序我都要改变sa数组，但是在排序的过程中我又要用到上一轮得到的sa数组，所以用y数组暂存上一轮的sa数组。
第二个for循环：同预处理中的第一个for循环作用一样，只是不用再分配桶了，也就是没有了x[i]=s[i]这一步。此时是按照预处理排序后的顺序进行遍历的，不是原始序列的顺序，就是i表示的排序为i的字符串，c数组里用的是字符串在原始序列中的下标，所以这里要转换一下，求排序为i的字符串在原始序列中的下标，其实这也就是sa数组的作用，用sa数组转换即可，这里用到的应该是上一轮排序得到的sa数组，所以我们此时用y数组，即x[y[i]]，这里就是排序后为i的字符串所在的桶，但是我这一轮是按照第二关键字进行排序的，所以应该有一个偏移，这个偏移加在哪里呢？自然是原始下标那里，所以应该是c[x[y[i]+k]]
第三个for循环：同预处理中的第二个for循环作用一样
第四个for循环：同预处理中的第三个for循环作用一样，因为i表示的是排序后的下标，所有多了转换的一步，同时sa[i]=j，这个j是原始序列的下标，所以有

sa[c[x[y[i]+k]]–] = y[i]

Arrays.fill(c, 0);
for(int i = 1;i <= n;i++) y[i] = sa[i];
for(int i = 1;i <= n;i++) c[x[y[i]+k]]++;
for(int i = 1;i <= m;i++) c[i] += c[i-1];
for(int i = n;i >= 1;i--) sa[c[x[y[i]+k]]--] = y[i];

按照第一关键字排序

这里同按照第二关键字排序排序一样，只是把偏移拿掉就可以了。

Arrays.fill(c, 0);
for(int i = 1;i <= n;i++) y[i] = sa[i];
for(int i = 1;i <= n;i++) c[x[y[i]]]++;
for(int i = 1;i <= m;i++) c[i] += c[i-1];
for(int i = n;i >= 1;i--) sa[c[x[y[i]]]--] = y[i];

重新分配桶

明确一点，只有在排序中相邻的两个字符串，才有可能相等，所以我们要判断排序中相邻的字符串就可以了，如何判断它们是否相等呢？看他们在上一轮中是否在同一个桶里。排序相邻的两个字符串sa[i],sa[i-1]，是否在同一个桶里

y[sa[i]] == y[sa[i-1]

，注意，我们这里不应该只比较第一关键字，还要比较第二关键字

y[sa[i]+k] == y[sa[i-1]+k]

，若相等则把当前桶号给他

x[sa[i]] = m;

，否则自己重新开辟一个桶

x[sa[i]] = ++m;

。注意：当分配的桶的个数和后缀字符串的个数相等时就说明我们已经完成了排序，直接退出循环即可，

if(m == n) break;。

for(int i = 1;i <= n;i++) y[i] = x[i];//存一下桶
m = 0;//重新给桶编号
for(int i = 1;i <= n;i++) {
	if(y[sa[i]] == y[sa[i-1]] && y[sa[i]+k] == y[sa[i-1]+k]) x[sa[i]] = m;
	else x[sa[i]] = ++m;
if(m == n) break;
}

例子

给一个字符串为aabaaaab，它的所有后缀字符串如下图左半部分所示，右半部分是按照所有后缀字符串的第一个字符排序后的结果

第一轮排序（k=1）：按照第二关键字进行排序后的结果如下图左半部分所示，右半部分是按照所有后缀字符串的第一关键字排序后的结果，

如下图所示，现在相当于对于每一个后缀字符串，按照前两个字符实现了排序，下图同时也展示了重新分配桶的结果。

第二轮排序（k=2）：接下来k变成2了，按照第二关键字进行排序后的结果如下图左半部分所示，右半部分是按照所有后缀字符串的第一关键字排序后的结果，我们在这里可以再理解一下c[x[y[i]+k]]++;，对于aaab，上一轮排序后的它对应的下标应该是3，那么y[3]得到的应该是5，也就是最初的那个下标，那么此时k=2，aaab的第一关键字是aa，第二关键字是ab，那我们看x[y[i]+k]=x[5+2]=x[7],原始下标为7的字符串是ab，而此时它的有效字符也恰好是ab，所以y[i]+k可以代表aaab的第二关键字。

我在学的时候有一个问题，在前一轮中我们按照每个后缀字符串的前两个字符实现了排序，在这一轮按照第二关键字进行排序时，我是怎么比较的第二关键字的大小的呢？其实一个字符串的第二关键字，也是某一个字符串的第一个关键字，如下图所示，而在上一轮排序时我已经确定了字符串的第一个关键字的大小

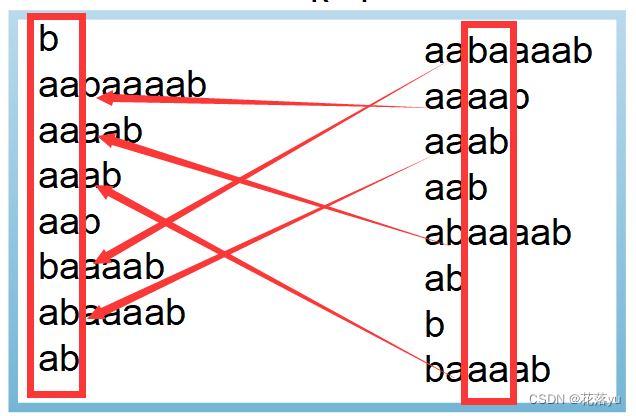
如下图所示，在第二轮排序完成后，会发现此时桶的个数恰好等于后缀字符串的个数，我们的排序结束！

完整代码如下

private static void get_sa() {
	// TODO Auto-generated method stub
	for(int i = 1;i <= n;i++) c[x[i]=s[i]]++;
	for(int i = 1;i <= m;i++) c[i] += c[i-1];
	for(int i = n;i >= 1;i--) sa[c[x[i]]--] = i;
	for(int k = 1;k <= n;k = k << 1) {
		Arrays.fill(c, 0);
		for(int i = 1;i <= n;i++) y[i] = sa[i];
		for(int i = 1;i <= n;i++) c[x[y[i]+k]]++;
		for(int i = 1;i <= m;i++) c[i] += c[i-1];
		for(int i = n;i >= 1;i--) sa[c[x[y[i]+k]]--] = y[i];
		Arrays.fill(c, 0);
		for(int i = 1;i <= n;i++) y[i] = sa[i];
		for(int i = 1;i <= n;i++) c[x[y[i]]]++;
		for(int i = 1;i <= m;i++) c[i] += c[i-1];
		for(int i = n;i >= 1;i--) sa[c[x[y[i]]]--] = y[i];
		
		for(int i = 1;i <= n;i++) y[i] = x[i];//存一下桶
		m = 0;//重新给桶编号
		for(int i = 1;i <= n;i++) {
			if(y[sa[i]] == y[sa[i-1]] && y[sa[i]+k] == y[sa[i-1]+k]) x[sa[i]] = m;
			else x[sa[i]] = ++m;
			if(m == n) break;
		}		
	}
}