双指针部分典型算法题（二）

? ? ? ? 上篇文章运用快慢指针解决问题，这篇文章中主要运用对撞指针的情况解决问题。

问题简述（11. 盛最多水的容器 - 力扣（LeetCode））：

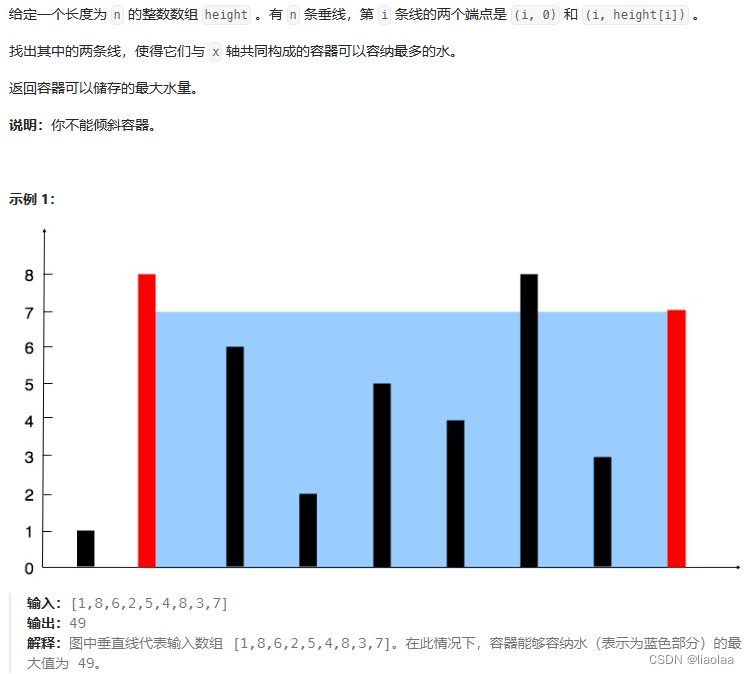
（思路一）直接暴力枚举，时间复杂度；

（思路二）进一步想，对于乱序数组我们一般可以先把它快排变为有序数组来处理，但这里这个思路行不通，因为即使我们确定了最高的两个容器的高，但容器的底在快排之后不好处理；

（思路三）如果我们使用指针分别从两边往中间遍历，可以发现随着我们的遍历容器的底会逐渐变小，所以我们只需要在遍历的过程中记录下我们容器的最大面积即可，时间复杂度。

附上思路三的具体代码：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0;
        int right = height.size()-1;
        int s = 0;
        while(left < right){
            if((right-left)*min(height[left],height[right]) > s){
                s = (right-left)*min(height[left],height[right]);
            }

            if(height[left] < height[right]){
                left++;
            }else{
                right--;
            }
        }
        return s;
    }
};

问题简述（611. 有效三角形的个数 - 力扣（LeetCode））：

?

（思路一）直接暴力枚举，时间复杂度；

（思路二）同样的，对于乱序数组，我们可以先使用快排（时间复杂度为），让其先变成有序数组，由于三角形的判定公式两边之和大于第三边（），我们可以先从一边开始遍历每一个c，每一次的遍历中，再用left和right指针从数组的0和n-2处开始相向遍历，时间复杂度。

附上思路二的具体代码：

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        sort(nums.begin(),nums.end());

        int count = 0;
        for(int i = nums.size()-1;i >= 0;--i){
            int left = 0;
            int right = i-1;
            while(left < right){
                if(nums[left] + nums[right] > nums[i]){
                    count += right - left; //这个[left,right]区间内的所有数都能组成三角形
                    --right;
                } else{
                    ++left; //不能组成三角形只可能是因为left值太小
                }
            }
        }
        return count;
    }
};

问题简述（1679. K 和数对的最大数目 - 力扣（LeetCode））：

?

容易被题目中的移出所误导，我们不需要将遍历过的移出数组，只需要保证不会再重复遍历到即可，所以我们仍可以先将乱序数组用快排处理为有序数组，再用left指针和right指针相向而行遍历，用k的值和两指针所指值之和的大小关系控制指针的移动，时间复杂度，由于快排的时间复杂度为，所以总的时间复杂度为。

附上的具体代码：

class Solution {
public:
    int maxOperations(vector<int>& nums, int k) {
        sort(nums.begin(),nums.end());

        int count = 0;
        int left = 0;
        int right = nums.size()-1;
        while(left < right){
            if(nums[left] + nums[right] > k){
                --right;
            } else if(nums[left] + nums[right] < k){
                ++left;
            } else{
                count++;
                --right;
                ++left;
            }
        }
        return count;
    }
};

问题简述（15. 三数之和 - 力扣（LeetCode））：

?

和上题同样的思路，时间复杂度接近。

附上的具体代码：

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(),nums.end());

        vector<vector<int>> arr;

        for(int i = nums.size()-1; i >= 0; --i){
            int left = 0;
            int right = i-1;
            while(left < right){
                if(nums[left] + nums[right] + nums[i] > 0){
                    --right;
                } else if(nums[left] + nums[right] + nums[i] < 0){
                    ++left;
                } else{
                    arr.push_back({nums[left],nums[right],nums[i]});
                    --right;
                    ++left;
                }
            }
        }
        return arr;
    }
};

根据我们的代码分析，其实这两个三元组所取到的0的位置是不一样的，确实可以说是没有取到重复元素的三元组，但取到的是重复值的三元组，我们如何去重呢？

（思路一）枚举当前所求出的三元组，没有重复值则添加为新的三元组，重复则不添加；

（思路二）我们可以在思路一的基础上，分开对i，left，right去重。

附上最后通过所有用例的代码：

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(),nums.end());

        vector<vector<int>> arr;
        for(int i = nums.size()-1; i >= 0; --i){
            int left = 0;
            int right = i-1;
            while(left < right){
                if(nums[left] + nums[right] + nums[i] > 0){
                    --right;
                } else if(nums[left] + nums[right] + nums[i] < 0){
                    ++left;
                } else{
                    arr.push_back({nums[left],nums[right],nums[i]});
                    --right;
                    ++left;

                    while(left < right && nums[left] == nums[left-1]){ //对left去重
                        ++left;
                    }
                    while(left < right && nums[right] == nums[right+1]){ //对right去重
                        --right;
                    }
                }
            }
            while(i > 0 && nums[i] == nums[i-1]){ //对i去重
                --i;
            }
        }
        return arr;
    }
};

问题简述（18. 四数之和 - 力扣（LeetCode））：

再看四数之和，其实就是三数之和的套娃，再将数组快排成有序数组之后，我们仍可以先固定一个数，问题就退化成三数之和问题。时间复杂度接近。

附上具体代码：

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        sort(nums.begin(),nums.end());

        vector<vector<int>> arr;
        for(int i = nums.size()-1; i >= 0; --i){
            for(int j = i-1; j >= 0; --j){
                int left = 0;
                int right = j-1;
                while(left < right){
                    if(nums[left] + nums[right] + nums[i] +nums[j] > target){
                        --right;
                    } else if(nums[left] + nums[right] + nums[i] +nums[j] < target){
                        ++left;
                    } else{
                        arr.push_back({nums[left],nums[right],nums[i],nums[j]});
                        --right;
                        ++left;

                        while(left < right && nums[left] == nums[left-1]){ //对left去重
                            ++left;
                        }
                        while(left < right && nums[right] == nums[right+1]){ //对right去重
                            --right;
                        }
                    }
                }
                while(j > 0 && nums[j] == nums[j-1]){ //对j去重
                    --j;
                }
            }
            while(i > 0 && nums[i] == nums[i-1]){ //对i去重
                --i;
            }
        }
        return arr;
    }
};

测试用例中会有数据溢出的情况，将int类型的数据改为long long型即可。