现代密码学 考点汇总（上）

写在最前面

字数超了，只能分为为两部分
很好，完美避开所有考点

考试范围

一、给一个简单的方案，判断是否cca安全

判断方式：要么证明是cca安全（通过规约），要么找一个攻击方式去攻击

一样一个题
1、对称加密、
2、消息认证码MAC
3、哈希函数、
4、非对称的多样加密的方案
【数字签名不考，因为和mac功能和证明方式、实验都类似】

二、随机预言机模型之下的简单应用

随机预言机性质、随机预言机模型之下的简单应用
性质之下构造函数的性质

---

笔记汇总

0. 规约证明

24. 规约证明

    • 我们现在站在敌手的角色来思考，希望解决“破解”加密方案这个问题，并且在此之前我们已经知道有个一“假设”问题是不可解决的；
    • 为了证明一个加密方案$\Pi$在假设$X$下是安全的，就是证明“破解”问题不可解。
    • 将解决“假设”$X$问题的算法${\mathcal{A}}^{\prime }$规约到“破解”$\Pi$的算法$\mathcal{A}$。如果加密方案可以被破解，则假设问题也可以解决。然而，由于假设问题是难以解决的，这导致矛盾，说明加密方案不可以被破解。
    • 先令一个概率多项式时间的算法$\mathcal{A}$能够以概率$\epsilon (n)$破解$\Pi$ ；
    • 假设：一个问题$X$是难以解决的，即不存在多项式时间算法来解决$X$；${\mathcal{A}}^{\prime }$是一个解决$X$的概率算法；
    • 规约：解决假设问题$X$可以通过破解加密方案$\Pi$，即将${\mathcal{A}}^{\prime }$规约到$\mathcal{A}$，${\mathcal{A}}^{\prime }$通过以$\mathcal{A}$作为子函数可以以概率$1/p(n)$有效地解决问题$X$；
    • 矛盾：若加密方案可以被有效破解，即$\epsilon (n)$是不可忽略的，则${\mathcal{A}}^{\prime }$可以以不可忽略的概率$\epsilon (n)/p(n)$解决问题$X$，这与假设矛盾，因而$\epsilon (n)$一定是可忽略的。

一个规约法证明PRG（伪随机生成器）的例子

25. 一个规约法证明PRG的例子

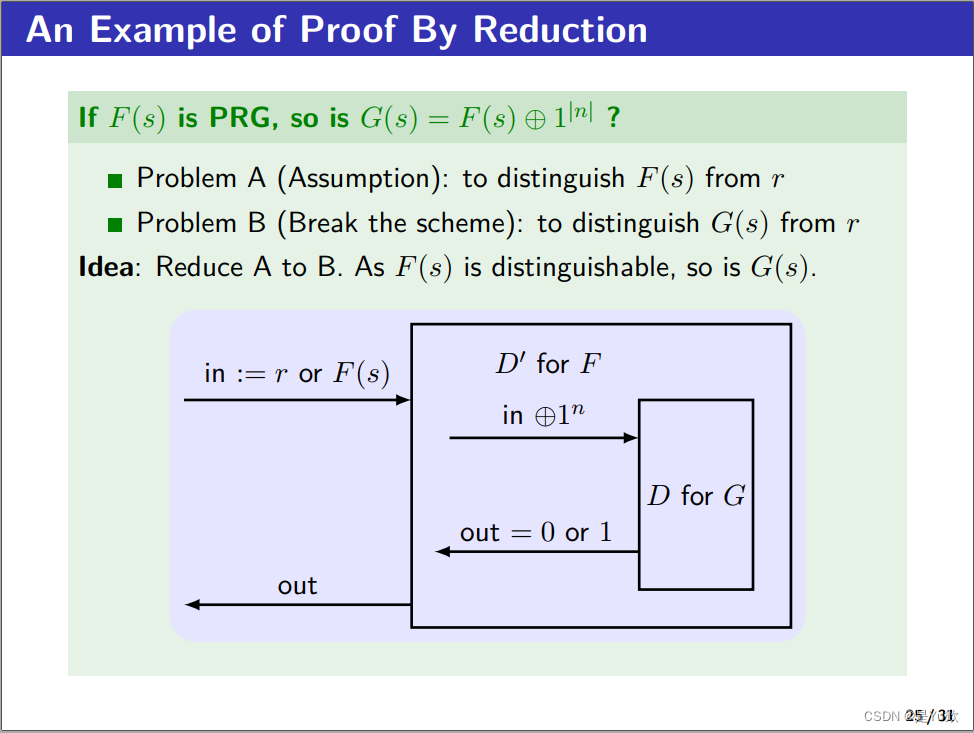
    • 假设$F$是PRG，证明$G$也是PRG。

    • 问题A：如何区分$F$；问题B：如何区分$G$；

    • 从A规约到B：区分$F$的算法输入按位取反后作为区分$G$的算法输入，区分$G$的算法输出作为区分$F$的算法输出。
      
      

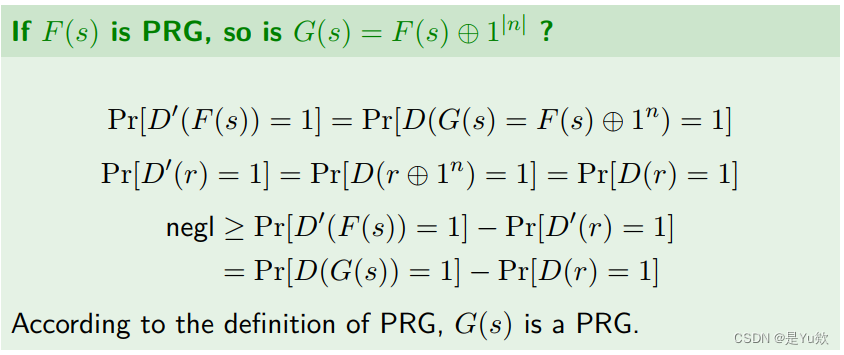
    • 由此，建立了不可区分定义中概率的联系。

定长加密方案，并证明不可区分加密方案

27. 一个安全的定长加密方案

    • $|G(k)|=?(|k|)$, m ∈ { 0 , 1 } ? ( n ) m \in \{0,1\}^{\ell(n)} m∈{0,1}?(n)， 一个PRG以长度为$n$的密钥作为种子，输出与明文相同长度的pad；
    • $\mathsf{Gen}$: k ∈ { 0 , 1 } n k \in \{0,1\}^n k∈{0,1}n，密钥作为种子，长度小于明文长度；
    • $\mathsf{Enc}$: $c:=G(k)\oplus m$，加密方法和一次一密一样；
    • $\mathsf{Dec}$: $m:=G(k)\oplus c$，解密也是；
    • 定理：该定长加密方案是窃听下不可区分的。
    • 直觉上，这个方案和一次一密是类似的，除了密钥更短并且用伪随机生成器生成的比特串来与明文异或。因为伪随机对于任何敌手都可以认为是真随机，所以对于敌手而言，该方案与一次一密是一样的。由此，我们得到了一个安全的加密方案，同时避免了一次一密的最大局限性——密钥过长。

28. 证明不可区分加密方案

    • 思路：区分伪随机性为难题假设，破解加密方案为规约的子函数。针对伪随机生成器$G$的区分器$D$以$\mathcal{A}$为子函数，使得当$\mathcal{A}$破解了$\Pi$则$D$可以区分出$G$，与$G$的伪随机性矛盾。注意这里我们用了符号$\tilde{\Pi }$来表示$\Pi$的一个变体，来刻画加密方案中可能使用了真随机串来加密；
    • 回顾针对伪随机生成器的区分器$D$的问题是，输入一个串$w$，输出一个比特；这里关键问题是输出的比特从何而来？
    • 将$D$规约到$\mathcal{A}$。回顾窃听者不可区分实验中，$\mathcal{A}$与一个挑战者进行3轮交互：
      1. $\mathcal{A}$选择两个不同明文$m_0,m_1$，并发送给挑战者；
      2. 挑战者生成密钥，并随机挑选一个明文$m_b$加密后得到挑战密文$c$，并发送给$\mathcal{A}$；
      3. $\mathcal{A}$输出对所加密明文的猜测$b^{\prime }$，若$b=b^{\prime }$，则$\mathcal{A}$成功；否则，失败；
    • 区分器$D$成为窃听不可区分实验中的挑战者，特别之处在于：在第2步，不需要生成密钥，而是直接以输入串$w$作为pad来加密，$c:=w\oplus m_b$；根据$w$的两种可能，分两种情况：
      • 当$w$是由$G$生成的，即伪随机串，则$c$就是加密方案$\Pi$中密文，$\mathcal{A}$面对的就是$\Pi$；
      • 当$w$是真随机串，则$c$不同于加密方案$\Pi$中密文，而与一次一密中一样，$\mathcal{A}$面对的就是$\tilde{\Pi }$一次一密；
    • 回答前面关于$D$输出什么的问题：破解加密方案的$\mathcal{A}$成功时，$D$输出1；否则，$D$输出0。

29. 证明不可区分加密方案（续）

    • 规约完毕，证明$\mathcal{A}$在实验中成功的概率是可忽略的
      • 当$w$为真随机串$r$，就是一次一密，$\mathrm{Pr}[D(r)=1]=\mathrm{Pr}[{\mathsf{PrivK}}_{\mathcal{A},\tilde{\Pi }}^{\mathsf{eav}}(n)=1]=\frac{1}{2}$；
      • 当$w$为伪随机串$G(k)$，$\mathrm{Pr}[D(G(k))=1]=\mathrm{Pr}[{\mathsf{PrivK}}_{\mathcal{A},\Pi }^{\mathsf{eav}}(n)=1]=\frac{1}{2}+\epsilon (n)$；
      • 根据伪随机生成器定义，上下两个公式相减，$\left|\mathrm{Pr}[D(r)=1]?\mathrm{Pr}[D(G(k))=1]\right|=\epsilon (n)\le \mathsf{negl}(n)$；
      • 所以$\epsilon (n)$是可忽略的，即$\Pi$是窃听者不可区分的。
    • 小结：通过规约将$\mathcal{A}$的不可区分实验成功的概率与$D$的区分器实验输出1的概率建立等式；分析输入真随机串时$D$输出1的概率（即不可区分实验成功概率）是1/2；根据PRG的定义，输入伪随机串时$D$输出1的概率（1/2+$\epsilon (n)$）与输入真随机串时$D$输出1的概率（1/2）的差异时可忽略的。

CCA安全加密方案

32. 选择密文攻击 Chosen-Ciphertext Attacks (CCA)

    • CCA不可区分实验 ${\mathsf{PrivK}}_{\mathcal{A},\Pi }^{\mathsf{cca}}(n)$:

      1. 挑战者生成密钥 $k\leftarrow \mathsf{Gen}(1^n)$；（为了下一步的预言机）
      2. $\mathcal{A}$ 被给予输入 $1^n$ 和对加密函数 ${\mathsf{Enc}}_k(?)$和解密函数${\mathsf{Dec}}_k(?)$的预言机访问（oracle access） ${\mathcal{A}}^{{\mathsf{Enc}}_k(?)}$ 和 ${\mathcal{A}}^{{\mathsf{Dec}}_k(?)}$，输出相同长度 $m_0,m_1$ ；
      3. 挑战者生成随机比特 b ← { 0 , 1 } b \gets \{0,1\} b←{0,1}，将挑战密文 $c\leftarrow {\mathsf{Enc}}_k(m_b)$ 发送给 $\mathcal{A}$；
      4. $\mathcal{A}$ 继续对除了挑战密文$c$之外的预言机的访问，输出$b^{\prime }$；如果$b^{\prime }=b$，则$\mathcal{A}$成功${\mathsf{PrivK}}_{\mathcal{A},\Pi }^{\mathsf{cca}}=1$，否则 0。

      定义：一个加密方案是CCA安全的，如果实验成功的概率与1/2的差异是可忽略的。

33. 理解CCA安全

    • 在现实世界中，敌手可以通过影响被解密的内容来实施CCA。如果通信没有认证，那么敌手可以以通信参与方的身份来发送特定密文。

    • CCA安全性意味着“non-malleability”（不可锻造性，即改变但不毁坏），不能修改密文来获得新的有效密文。

    • 之前的方案中没有CCA安全，因为都不是不可锻造。

    • 对基于PRF的CPA安全加密方案的CCA攻击：

      • $\mathcal{A}$ 获得挑战密文 $c=?r,F_k(r)\oplus m_b?$，并且查询与$c$只相差了一个翻转的比特的密文$c^{\prime }$，那么

        $m^{\prime }=c^{\prime }\oplus F_k(r)$ 应该与 $m_b$ 除了什么之外都相同？（见下方补充）

    • 问题：上述操作模式也不是CCA安全的（作业）

    • 由此，可以总结出CCA下敌手的常用策略：

      • 修改挑战密文$c$为$c^{\prime }$，并查询解密预言机得到$m^{\prime }$
      • 根据关系，由$m^{\prime }$来猜测被加密明文$m_b$

补充

在这个情况下，$\mathcal{A}$ 获得了挑战密文 $c=?r,F_k(r)\oplus m_b?$ 并查询了一个只在一个比特上与 $c$ 不同的密文 $c^{\prime }$。我们来分析一下 $m^{\prime }=c^{\prime }\oplus F_k(r)$ 与 $m_b$ 的关系。

首先，我们明确 $c$ 的构成：

• $c$ 包含两个部分：一个随机数 $r$ 和使用密钥 $k$ 的函数 $F_k(r)$ 与明文 $m_b$ 的异或结果。
• 因此，$c=?r,F_k(r)\oplus m_b?$。

现在，如果 $\mathcal{A}$ 查询了一个与 $c$ 只在一个比特上不同的密文 $c^{\prime }$，那么 $c^{\prime }$ 也可以写成两部分，但其中一部分与 $c$ 有一个比特的差异。这个差异可以在 $r$ 部分，也可以在 $F_k(r)\oplus m_b$ 部分。

当 $\mathcal{A}$ 计算 $m^{\prime }=c^{\prime }\oplus F_k(r)$ 时，他们实际上是在解开 $F_k(r)\oplus m_b$ 的异或操作。这是因为异或操作是可逆的，且当两次使用相同的值时会取消彼此的效果（即 $A\oplus B\oplus B=A$）。

因此，如果 $c^{\prime }$ 的变化发生在 $F_k(r)$ 部分，则 $m^{\prime }$ 将与 $m_b$ 完全相同，因为 $F_k(r)$ 部分的变化被异或操作取消了。但如果变化发生在 $r$ 部分，则这个变化不会影响到 $F_k(r)\oplus m_b$ 部分，因此 $m^{\prime }$ 将与 $m_b$ 在一个比特上不同。

综上所述，$m^{\prime }$ 与 $m_b$ 将在以下方面相同：

• 如果变化发生在 $F_k(r)$ 部分，那么 $m^{\prime }$ 与 $m_b$ 完全相同。
• 如果变化发生在 $r$ 部分，那么 $m^{\prime }$ 与 $m_b$ 除了那个翻转的比特之外都相同。

1. 对称加密

CPA安全实验、预言机访问（oracle access）

11. CPA安全实验

    • CPA不可区分实验 ${\mathsf{PrivK}}_{\mathcal{A},\Pi }^{\mathsf{cpa}}(n)$:
      1. 挑战者生成密钥 $k\leftarrow \mathsf{Gen}(1^n)$；（这里与窃听者不可区分实验相比，密钥的生成提前了，这是为了下一步提供加密预言机）
      2. $\mathcal{A}$ 被给予输入 $1^n$ 和对加密函数 ${\mathsf{Enc}}_k(?)$的预言机访问（oracle access） ${\mathcal{A}}^{{\mathsf{Enc}}_k(?)}$ ，输出相同长度 $m_0,m_1$ ；
      3. 挑战者生成随机比特 b ← { 0 , 1 } b \gets \{0,1\} b←{0,1}，将挑战密文 $c\leftarrow {\mathsf{Enc}}_k(m_b)$ 发送给 $\mathcal{A}$；
      4. $\mathcal{A}$ 继续对 ${\mathsf{Enc}}_k(?)$的预言机的访问，输出$b^{\prime }$；如果$b^{\prime }=b$，则$\mathcal{A}$成功${\mathsf{PrivK}}_{\mathcal{A},\Pi }^{\mathsf{cpa}}=1$，否则 0。
    • 敌手对加密函数预言机访问是指，敌手以任意明文作为输入，可以从预言机得到对应密文。此处，密钥是已经提前生成的，因此才能通过加密函数预研机得到密文，但仍对敌手保密。预言机是一个形象的比喻，它是一个黑盒，只接收输入并返回输出；访问者不需要了解其内部构造。
    • 该实验与窃听者不可区分实验的区别在于，敌手可访问加密预言机，在实验过程中始终可以，包括在产生两个明文阶段，以及在收到挑战密文后猜测被加密明文阶段，获得任意明文被同一密钥加密的密文；而且密文是逐个获得，可以根据之前的明文和密文对来“适应性地”构造新的查询。
    • CPA敌手比多重加密的敌手更“强大”，因为多重加密敌手是可以一次性地获得一组密文，而CPA敌手可以根据已经获得的明文和密文“多次适应性地”再次获得密文。

12. CPA安全

    • $\Pi$ 是CPA不可区分加密方案 (CPA安全的)，如果任意概率多项式时间算法$\mathcal{A}$，存在可忽略的函数$\mathsf{negl}$使得，

      $\mathrm{Pr}\left[{\mathsf{PrivK}}_{\mathcal{A},\Pi }^{\mathsf{cpa}}(n)=1\right]\le \frac{1}{2}+\mathsf{negl}(n)$

    • 定理：CPA安全也是多重加密安全的。证明略。直觉上，CPA敌手比多重加密敌手更强大。

    • 之前的方案也难以实现CPA安全；

    • 多重加密安全意味着CPA安全？（作业）显然是否定的。那么，思考两种安全定义的区别成为解题的关键。

操作模式

伪随机函数PRF

13. 伪随机函数（Pseudorandom Function）概念

    • 为了实现CPA安全，之前的PRG提供的随机性不够用了，需要新的数学工具为加密提供额外的随机性。为此引入伪随机函数（PRF），是对伪PRG的泛化：PRG从一个种子生成一个随机串，PRF从一个key生成一个函数；
    • 带密钥的函数Keyed function F : { 0 , 1 } ? × { 0 , 1 } ? → { 0 , 1 } ? F : \{0,1\}^* \times \{0,1\}^* \to \{0,1\}^* F:{0,1}?×{0,1}?→{0,1}?
      • F k : { 0 , 1 } ? → { 0 , 1 } ? F_k : \{0,1\}^* \to \{0,1\}^* Fk?:{0,1}?→{0,1}?, $F_k(x)\stackrel{\text{def}}{=}F(k,x)$
      • 两个输入到一个输出，看上去像，但不是加密函数；输入key，得到一个一输入到一输出的函数；
    • 查表Look-up table $f$: { 0 , 1 } n → { 0 , 1 } n \{0,1\}^n \to \{0,1\}^n {0,1}n→{0,1}n 需要多少比特信息存储？
      • 查表是一个直接描述输入与输出间映射的表格，一个条目对应一个输入与一个输出；当该映射是随机产生的，是一个真随机函数；
    • 函数族Function family ${\mathsf{Func}}_n$: 包含所有函数 { 0 , 1 } n → { 0 , 1 } n \{0,1\}^n \to \{0,1\}^n {0,1}n→{0,1}n. $|{\mathsf{Func}}_n|=2^{n?2^n}$
      • 一个PRF是函数族中一个子集，key确定下的PRF是函数族中一个元素，一个查表是函数族中一个元素；
    • 长度保留Length Preserving: ${?}_{key}(n)={?}_{in}(n)={?}_{out}(n)=n$；密钥长度与函数输入、输出长度相同为$n$；没有特殊说明时，只讨论长度保留的函数；

14. 伪随机函数定义

    • 直觉上，一个PRF生成的带密钥的函数与从函数族中随机选择的真随机函数（查表）之间是不可区分的；然而，一个真随机函数具有指数长度，无法“预先生成”，只能“on-the-fly”（边运行、边生成）的使用，引入一个对函数$\mathcal{O}$的确定性的预言机访问（oracle access）$D^{\mathcal{O}}$。
    • 这里的预言机是一个抽象的函数。访问预言机，就是给出任意输入，得到该函数的输出。访问预言机的能力不包括了解正在访问的预言机具体内部构造。
    • 一个带密钥的函数是一个伪随机函数（PRF），对任意PPT区分器$D$，$\left|\mathrm{Pr}[D^{F_k(?)}(1^n)=1]?\mathrm{Pr}[D^{f(?)}(1^n)=1]\right|\le \mathsf{negl}(n)$，其中$f$是${\mathsf{Func}}_n$中随机函数。
      • 这里区分器$D$是一个算法，可以访问预言机，但并不知道预言机背后是什么。
      • 这里不可区分性关键是，对真随机查表和伪随机函数，区分器输出相同结果概率的差异。区分器输出1或0本身没有，也无需，有特定语义。
    • PRF和PRG的关系在后面会学习，可以由PRG来构造PRF。

PRF例题：一个固定长度的一次一密方案是一个PRF吗？

15. PRF例题

    • 问题一个固定长度的一次一密方案是一个PRF吗？
    • 对于一个PRF，在密钥保密和没有预言机访问时，给指定输入，能以不可忽略的概率猜测输出相关信息吗？
    • 如果是PRF，则给出该函数与查表的相似性；否则，给出一个区分器可以区分出该函数不是随机的。

16. 以PRF实现CPA安全

    • 新随机串 $r$，每次新生成一个随机串；
    • $F_k(r)$: $|k|=|m|=|r|=n$. 长度保留；
    • $\mathsf{Gen}$: k ∈ { 0 , 1 } n k \in \{0,1\}^n k∈{0,1}n.
    • $\mathsf{Enc}$: $s:=F_k(r)\oplus m$, $c:=?r,s?$. 密文包括两部分新随机串，以及异或输出；
    • $\mathsf{Dec}$: $m:=F_k(r)\oplus s$.
    • 定理：上述方案是CPA安全的。

从PRF到CPA安全的证明

17. 从PRF到CPA安全的证明

    • 思路：从PRF的区分器算法$\mathcal{D}$规约到加密方案敌手算法$\mathcal{A}$，区分器$\mathcal{D}$作为敌手$\mathcal{A}$的挑战者，敌手$\mathcal{A}$实验成功时区分器$\mathcal{D}$输出1。分两种情况，当输入真随机函数$f$时，相当于一次一密；当输入伪随机函数$F_k$时，为加密方案。
    • 规约：$\mathcal{D}$输入预言机，输出一个比特；$\mathcal{A}$的加密预言机访问通过$\mathcal{D}$的预言机$\mathcal{O}$来提供，$c:=?r,\mathcal{O}(r)\oplus m?$；$\mathcal{D}$输出1，当$\mathcal{A}$在实验中成功。
      • 这里有两个预言机：$\mathcal{D}$访问的预言机$\mathcal{O}$，$\mathcal{A}$访问的加密预言机${\mathsf{Enc}}_k$，后者不能直接访问前者的预言机。

18. 从PRF到CPA安全的证明（续）

    • 考虑真随机函数$f$的情况，分析不可区分实验成功概率$\mathrm{Pr}[{\mathsf{PrivK}}_{\mathcal{A},\tilde{\Pi }}^{\mathsf{cpa}}(n)=1]=\mathrm{Pr}[\mathsf{Break}]$。敌手$\mathcal{A}$访问加密预言机可以获得多项式$q(n)$个明文与密文对的查询结果并得到随机串和pad { < r i , f ( r i ) > } \{ \left< r_i, f(r_i) \right> \} {?ri?,f(ri?)?}；当收到挑战密文$c=?r_c,s:=f(r_c)\oplus m_b?$时，根据之前查询结果中随机串是否与挑战密文中随机串相同，分为两种情况：

      • 当有相同随机串时，根据$r$可以得到$f(r_c)$，$m_b=f(r_c)\oplus s$，但这种情况发生的概率$q(n)/2^n$是可忽略的；
      • 当没有相同随机串时，输出是随机串，相当于一次一密，成功概率=1/2；

    • $\mathrm{Pr}[D^{F_k(?)}(1^n)=1]=\mathrm{Pr}[{\mathsf{PrivK}}_{\mathcal{A},\Pi }^{\mathsf{cpa}}(n)=1]=\frac{1}{2}+\epsilon (n).$

    • $\mathrm{Pr}[D^{f(?)}(1^n)=1]=\mathrm{Pr}[{\mathsf{PrivK}}_{\mathcal{A},\tilde{\Pi }}^{\mathsf{cpa}}(n)=1]=\mathrm{Pr}[\mathsf{Break}]\le \frac{1}{2}+\frac{q(n)}{2^n}.$

    • $\mathrm{Pr}[D^{F_k(?)}(1^n)=1]?\mathrm{Pr}[D^{f(?)}(1^n)=1]\ge \epsilon (n)?\frac{q(n)}{2^n}.$ 根据伪随机函数定义，$\epsilon (n)$ 是可忽略的.

    • 小结：通过规约将$\mathcal{A}$的不可区分实验成功的概率与$D$的区分器实验输出1的概率建立等式；分析输入真随机函数预言机时$D$输出1的概率（即不可区分实验成功概率）是1/2+一个可忽略函数；根据PRF的定义，输入伪随机函数预言机时$D$输出1的概率（1/2+$\epsilon (n)$）与输入真随机函数预言机时$D$输出1的概率（1/2）的差异时可忽略的。

19. CPA安全例题

    • ${\mathsf{Enc}}_k(m)=PRG(k\Vert r)\oplus m$, $r$ 是新的随机串。这是CPA安全的吗？
    • 从PRF到CPA安全：变长消息
    • 对于任意长度消息 $m=m_1,\dots ,m_{?}$，$c:=?r_1,F_k(r_1)\oplus m_1,r_2,F_k(r_2)\oplus m_2,\dots ,r_{?},F_k(r_{?})\oplus m_{?}?$
    • 推论：如果$F$是一个 PRF，那么 $\Pi$ 对任意长度消息是 CPA 安全的。
    • 问题：这个方案有什么缺点？
    • 有效性: $|c|=2|m|$. 密文长度是明文长度的二倍，并且需要大量的真随机串。

伪随机排列PRP

20. 伪随机排列（Pseudorandom Permutations）

    • 为了提高对任意长度消息加密的效率，以及更高级的加密基础工具，学习伪随机排列PRP的概念；

    • 双射 Bijection: $F$ 是一到一的（一个输入对应一个唯一输出）且满射（覆盖输出集中每个元素）；

    • 排列 Permutation: 一个从一个集合到自身的双射函数；

    • 带密钥的排列 Keyed permutation: $?k,F_k(?)$是排列；类似带密钥的函数；

    • $F$ 是一个双射 $?F^{?1}$ 是一个双射；函数和逆函数都是双射；

    • 定义：一个有效的带密钥的排列 $F$ 是PRP，如果对于任意PPT的区分器$D$，

      $\left|\mathrm{Pr}[D^{F_k(?),F_k^{?1}(?)}(1^n)=1]?\mathrm{Pr}[D^{f(?),f^{?1}(?)}(1^n)=1]\right|\le \mathsf{negl}(n)$

    • 问题：一个PRP也是一个PRF吗？

21. PRP例题

    • 对1比特的PRP、PRF的分析；
    • 交换引理：如果 $F$ 是一个 PRP 并且 ${?}_{in}(n)\ge n$，那么 $F$ 也是一个 PRF。
      • 一个随机排列和一个查表是不可取分的，PRP和随机排列不可取分，因此，PRP和查表是不可取分的。

22. 操作模式概念（Modes of Operation）

    • 操作模式是使用PRP或PRF来加密任意长度消息的方法；
    • 操作模式是从PRP或PRF来构造一个PRG的方法；
    • 将一个消息分成若干等长的块（分组，block），每个块以相似方式处理；

23. Electronic Code Book (ECB) 模式

    • 在窃听者出现时，是否是不可区分的？
    • $F$ 可以是任意PRF吗？

24. 对ECB的攻击

    • 为什么仍然可以识别企鹅？

25. Cipher Block Chaining (CBC) 模式

    • $IV$初始向量，一个新的随机串；
    • 是CPA的吗？可并行化吗？F可以是任意PRF吗？

26. Output Feedback (OFB) Mode模式

    • 是CPA安全吗？可并行化吗？F可以是任意PRF吗？

27. Counter (CTR) Mode模式

    • $ctr$是一个初始向量，并且逐一增加；
    • 是CPA安全吗？可并行化吗？F可以是任意PRF吗？

28. CTR模式是CPA安全
    

    • 定理：如果$F$是一个PRF，那么随机CTR模式是CPA安全的。

    • 证明：其安全性与之前基于PRF的CPA安全证明类似，从PRF的伪随机假设规约到CPA安全加密方案。其中，对$ctr$的安全性直觉在于，$ctr$也是在加密前不可预测的，且每个块所用$ctr$都是不同的；

    • 当加密预言机是由真随机查表构成时，敌手多次访问加密预言机得到的$ctr$序列与挑战密文的$ctr$序列之间有重叠的概率$\frac{2q(n{)}^2}{2^n}$是可以忽略的；若没有重叠，则相当于一次一密；

    • 规约与之前证明基于PRF的CPA安全加密方案一样，证明过程也类似。

29. 初始向量不应该可预测

    • 如果$IV$是可预测的，那么CBC/OFB/CTR模式不是CPA安全的。
    • 为什么？（作业）
    • 在SSL/TLS 1.0中的漏洞：记录$\#i$的$IV$是上一个记录$\#(i?1)$的密文块。
    • OpenSSL中API：需要用户输入$IV$，但$IV$应在函数内实现。当$IV$不充分随机时不安全。

30. 非确定性加密

    • 有三种通用的实现CPA安全的非确定性加密方法：
    • 随机化的：$r$随机生成，如构造5；需要更多熵，长密文
    • 有状态的：$r$为计数器，如CTR模式；需要通信双方同步计数器
    • 基于Nonce的：$r$只用一次；需要保证只用一次，长密文

CCA安全加密方案

32. 选择密文攻击 Chosen-Ciphertext Attacks (CCA)

    • CCA不可区分实验 ${\mathsf{PrivK}}_{\mathcal{A},\Pi }^{\mathsf{cca}}(n)$:

      1. 挑战者生成密钥 $k\leftarrow \mathsf{Gen}(1^n)$；（为了下一步的预言机）
      2. $\mathcal{A}$ 被给予输入 $1^n$ 和对加密函数 ${\mathsf{Enc}}_k(?)$和解密函数${\mathsf{Dec}}_k(?)$的预言机访问（oracle access） ${\mathcal{A}}^{{\mathsf{Enc}}_k(?)}$ 和 ${\mathcal{A}}^{{\mathsf{Dec}}_k(?)}$，输出相同长度 $m_0,m_1$ ；
      3. 挑战者生成随机比特 b ← { 0 , 1 } b \gets \{0,1\} b←{0,1}，将挑战密文 $c\leftarrow {\mathsf{Enc}}_k(m_b)$ 发送给 $\mathcal{A}$；
      4. $\mathcal{A}$ 继续对除了挑战密文$c$之外的预言机的访问，输出$b^{\prime }$；如果$b^{\prime }=b$，则$\mathcal{A}$成功${\mathsf{PrivK}}_{\mathcal{A},\Pi }^{\mathsf{cca}}=1$，否则 0。

      定义：一个加密方案是CCA安全的，如果实验成功的概率与1/2的差异是可忽略的。

33. 理解CCA安全

    • 在现实世界中，敌手可以通过影响被解密的内容来实施CCA。如果通信没有认证，那么敌手可以以通信参与方的身份来发送特定密文。下一页有具体真实案例。

    • CCA安全性意味着“non-malleability”（不可锻造性，即改变但不毁坏），不能修改密文来获得新的有效密文。

    • 之前的方案中没有CCA安全，因为都不是不可锻造。

    • 对基于PRF的CPA安全加密方案的CCA攻击：

      • $\mathcal{A}$ 获得挑战密文 $c=?r,F_k(r)\oplus m_b?$，并且查询与$c$只相差了一个翻转的比特的密文$c^{\prime }$，那么

        $m^{\prime }=c^{\prime }\oplus F_k(r)$ 应该与 $m_b$ 除了什么之外都相同？（见下方的补充）

    • 问题：上述操作模式也不是CCA安全的（作业）

    • 由此，可以总结出CCA下敌手的常用策略：

      • 修改挑战密文$c$为$c^{\prime }$，并查询解密预言机得到$m^{\prime }$
      • 根据关系，由$m^{\prime }$来猜测被加密明文$m_b$

补充

在这个情况下，$\mathcal{A}$ 获得了挑战密文 $c=?r,F_k(r)\oplus m_b?$ 并查询了一个只在一个比特上与 $c$ 不同的密文 $c^{\prime }$。我们来分析一下 $m^{\prime }=c^{\prime }\oplus F_k(r)$ 与 $m_b$ 的关系。

首先，我们明确 $c$ 的构成：

• $c$ 包含两个部分：一个随机数 $r$ 和使用密钥 $k$ 的函数 $F_k(r)$ 与明文 $m_b$ 的异或结果。
• 因此，$c=?r,F_k(r)\oplus m_b?$。

现在，如果 $\mathcal{A}$ 查询了一个与 $c$ 只在一个比特上不同的密文 $c^{\prime }$，那么 $c^{\prime }$ 也可以写成两部分，但其中一部分与 $c$ 有一个比特的差异。这个差异可以在 $r$ 部分，也可以在 $F_k(r)\oplus m_b$ 部分。

当 $\mathcal{A}$ 计算 $m^{\prime }=c^{\prime }\oplus F_k(r)$ 时，他们实际上是在解开 $F_k(r)\oplus m_b$ 的异或操作。这是因为异或操作是可逆的，且当两次使用相同的值时会取消彼此的效果（即 $A\oplus B\oplus B=A$）。

因此，如果 $c^{\prime }$ 的变化发生在 $F_k(r)$ 部分，则 $m^{\prime }$ 将与 $m_b$ 完全相同，因为 $F_k(r)$ 部分的变化被异或操作取消了。但如果变化发生在 $r$ 部分，则这个变化不会影响到 $F_k(r)\oplus m_b$ 部分，因此 $m^{\prime }$ 将与 $m_b$ 在一个比特上不同。

综上所述，$m^{\prime }$ 与 $m_b$ 将在以下方面相同：

• 如果变化发生在 $F_k(r)$ 部分，那么 $m^{\prime }$ 与 $m_b$ 完全相同。
• 如果变化发生在 $r$ 部分，那么 $m^{\prime }$ 与 $m_b$ 除了那个翻转的比特之外都相同。

填充预言机Padding-Oracle攻击真实案例

34. Padding-Oracle（填充预言机）攻击真实案例

    • CAPTCHA服务商为Web网站提供验证用户是否为人类的服务。为此，一个CAPTCHA服务器与Web服务器间事先共享一个密钥$k$，服务工作原理如下：
      1. 当Web服务器验证用户是否为人类时，生成一个消息$w$并以$k$加密，向用户发送一个密文$En{c}_k(w)$；
      2. 用户将密文$En{c}_k(w)$转发给CAPTCHA服务器；（可实施填充预言机攻击）
      3. CAPTCHA服务器用密钥$k$将密文解密，根据解密结果返回给用户信息：一个由$w$生成的图像，或者坏填充错误；
      4. 用户根据图像获得 $w$ 并将 $w$ 发送给Web服务器。
    • 在第2步，当恶意用户可以利用CAPTCHA服务器会返回给用户坏填充错误这一漏洞，来实施填充错误攻击。

35. Padding-Oracle（填充预言机）攻击

    • 在PKCS #5 padding（填充）标准中，为了将一个消息的长度“填充”到块长度的整数倍，在最后一个块中填充$b$个字节的$b$；必要时，添加一个哑块（dummy block，不包含消息的一个填充块）。存在一种攻击手段：当填充错误时，解密服务器返回一个“坏填充错误”，这相当于提供了一个解密预言机，最终可以获得整个明文；
    • 具体攻击原理：
      • 更改密文（包含$IV$部分）并发送给解密服务器；
      • 一旦触发了“坏填充错误”，则说明对密文的更改导致了填充部分内容的更改；否则，对密文的更改导致了原明文部分的更改；
      • 通过仔细修改密文来控制填充部分，从而获得消息长度和内容。

36. 填充预言机攻击：获得消息长度

    • 攻击的第一步判断消息是否为空：在单个块的CBC中，通过更改$IV$的首个字节，攻击者能够获知是否$m$是否为空。因为如果$m$是空的话，更改$IV$首个字节将更改解密出的填充内容，解密服务器就会返回坏填充错误（1比特信息），具体分析如下：
      • 如果$m$是空的，那么明文会添加一个哑块 { b } b \{b\}^b {b}b；
      • PRP的输入为 I V ⊕ { b } b IV\oplus \{b\}^b IV⊕{b}b；设$IV$的首个字节为$x$，则PRP的输入为 ( x ⊕ b ) ∥ ( { ? } b ? 1 ⊕ { b } b ? 1 ) (x \oplus b) \| (\{\cdot\}^{b-1} \oplus \{b\}^{b-1}) (x⊕b)∥({?}b?1⊕{b}b?1)；
      • 将$IV$的首个字节从$x$改成$y$变为 y ∥ ( { ? } b ? 1 ) y \| (\{\cdot\}^{b-1}) y∥({?}b?1)，不改变$c_1$解密得到的PRP的输入不会变，而解密出的明文会改变为 ( x ⊕ y ⊕ b ) ∥ { b } b ? 1 (x \oplus y \oplus b) \| \{b\}^{b-1} (x⊕y⊕b)∥{b}b?1；
      • 上述明文首个字节一定不是$b$，这是填充格式错误，会触发服务器返回错误；
      • 如果上面的尝试没有触发错误，那么说明消息非空；下一步，发现消息长度是否为1字节，方法与上一步一样，区别在于只改变$IV$的第2个字节；如此继续，获得消息的长度；（作业）

37. 填充预言机攻击：获得消息内容

    • 一旦获得消息的长度，也就知道了填充的长度$b$，采用下面的方法来获得消息的最后一个字节内容，进而获得整个消息；
    • 更改密文中倒数第二块，来获得消息的最后一个字节$s$；
    • 明文的最后一个块 m l a s t = ? s ∥ { b } b m_{last} = \cdots s \| \{b\}^{b} mlast?=?s∥{b}b，密文的倒数第二个块 c l a s t ? 1 = ? t ∥ { ? } b c_{last-1} = \cdots t \| \{\cdot \}^{b} clast?1?=?t∥{?}b；
    • 最后一块的PRP输入为 c l a s t ? 1 ⊕ m l a s t = ? ( s ⊕ t ) ∥ ( { b } b ⊕ { ? } b ) c_{last-1} \oplus m_{last} = \cdots (s \oplus t) \| (\{b\}^b \oplus \{\cdot \}^{b}) clast?1?⊕mlast?=?(s⊕t)∥({b}b⊕{?}b)；
    • 敌手更改 $c_{last?1}$ 为 c l a s t ? 1 ′ = ? u ∥ ( { ? } b ⊕ { b } b ⊕ { b + 1 } b ) c_{last-1}' = \cdots u \| (\{\cdot \}^{b} \oplus \{b\}^{b} \oplus \{b+1\}^{b}) clast?1′?=?u∥({?}b⊕{b}b⊕{b+1}b)；其中，$u$是敌手猜测的某个字节；
    • 解密获得最后一块明文 m l a s t ′ = c l a s t ? 1 ⊕ m l a s t ⊕ c l a s t ? 1 ′ = ? ( s ⊕ t ⊕ u ) ∥ { b + 1 } b m'_{last} = c_{last-1} \oplus m_{last} \oplus c_{last-1}' = \cdots (s \oplus t \oplus u)\| \{ b+1 \}^b mlast′?=clast?1?⊕mlast?⊕clast?1′?=?(s⊕t⊕u)∥{b+1}b；
    • 如果没有返回坏填充错误，那么意味着填充了$b+1$个字节的$b+1$，所以 $s\oplus t\oplus u=(b+1)$ ，而 $s=t\oplus u\oplus (b+1)$ 。

38. 总结

    • 略