Pythpn实现匀速直线运动图像复原

匀速直线运动图像复原

1.代码

1.主要是使用逆滤波和维纳滤波进行图像复原，以及两者的一个对比

import matplotlib.pyplot as plt
import numpy as np
from numpy import fft
import math
import cv2


# 仿真运动模糊
def motion_process(image_size, motion_angle):
    PSF = np.zeros(image_size)
    print(image_size)
    center_position = (image_size[0] - 1) / 2
    print(center_position)

    slope_tan = math.tan(motion_angle * math.pi / 180)
    slope_cot = 1 / slope_tan
    if slope_tan <= 1:
        for i in range(15):
            offset = round(i * slope_tan)  # ((center_position-i)*slope_tan)
            PSF[int(center_position + offset), int(center_position - offset)] = 1
        return PSF / PSF.sum()  # 对点扩散函数进行归一化亮度
    else:
        for i in range(15):
            offset = round(i * slope_cot)
            PSF[int(center_position - offset), int(center_position + offset)] = 1
        return PSF / PSF.sum()


# 对图片进行运动模糊
def make_blurred(input, PSF, eps):
    input_fft = fft.fft2(input)  # 进行二维数组的傅里叶变换
    PSF_fft = fft.fft2(PSF) + eps
    blurred = fft.ifft2(input_fft * PSF_fft)
    blurred = np.abs(fft.fftshift(blurred))
    return blurred


def inverse(input, PSF, eps):  # 逆滤波
    input_fft = fft.fft2(input)
    PSF_fft = fft.fft2(PSF) + eps  # 噪声功率，这是已知的，考虑epsilon
    result = fft.ifft2(input_fft / PSF_fft)  # 计算F(u,v)的傅里叶反变换
    result = np.abs(fft.fftshift(result))
    return result


def wiener(input, PSF, eps, K=0.01):  # 维纳滤波，K=0.01
    input_fft = fft.fft2(input)
    PSF_fft = fft.fft2(PSF) + eps
    PSF_fft_1 = np.conj(PSF_fft) / (np.abs(PSF_fft) ** 2 + K)
    result = fft.ifft2(input_fft * PSF_fft_1)
    result = np.abs(fft.fftshift(result))
    return result


image = cv2.imread('lena2.jpg')
image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)  # 转换为灰度图像
img_h = image.shape[0]
img_w = image.shape[1]
plt.figure(1)
plt.xlabel("Original Image")
plt.gray()
plt.imshow(image)  # 显示原图像

plt.figure(2)
plt.gray()
# 进行运动模糊处理
PSF = motion_process((img_h, img_w), 60)
blurred = np.abs(make_blurred(image, PSF, 1e-3))

plt.subplot(231)
plt.xlabel("Motion blurred")
plt.imshow(blurred)

result = inverse(blurred, PSF, 1e-3)  # 逆滤波
plt.subplot(232)
plt.xlabel("inverse deblurred")
plt.imshow(result)

result = wiener(blurred, PSF, 1e-3)  # 维纳滤波
plt.subplot(233)
plt.xlabel("wiener deblurred(k=0.01)")
plt.imshow(result)

blurred_noisy = blurred + 0.1 * blurred.std() * \
                np.random.standard_normal(blurred.shape)  # 添加噪声,standard_normal产生随机的函数

plt.subplot(234)
plt.xlabel("motion & noisy blurred")
plt.imshow(blurred_noisy)  # 显示添加噪声且运动模糊的图像

result = inverse(blurred_noisy, PSF, 0.1 + 1e-3)  # 对添加噪声的图像进行逆滤波
plt.subplot(235)
plt.xlabel("inverse deblurred")
plt.imshow(result)

result = wiener(blurred_noisy, PSF, 0.1 + 1e-3)  # 对添加噪声的图像进行维纳滤波
plt.subplot(236)
plt.xlabel("wiener deblurred(k=0.01)")
plt.imshow(result)

plt.show()

2. 没有这个库的，需要安装这个库

3.执行结果

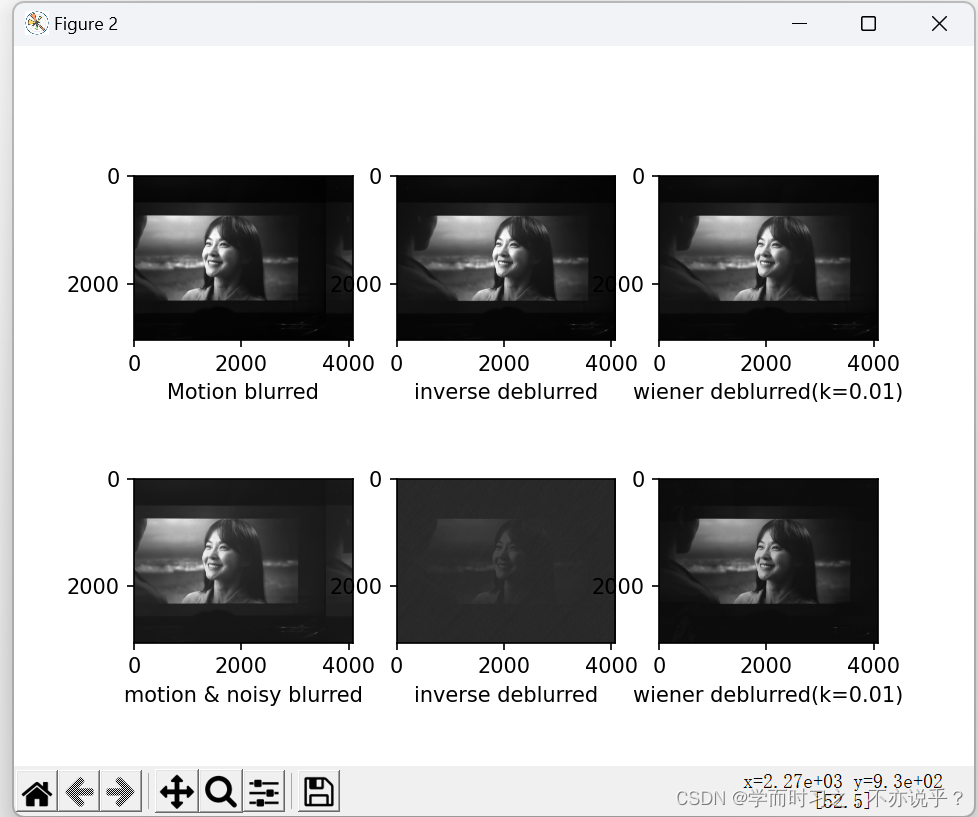
从图中可以看出：图1添加了运动模糊的图像比原图像要模糊的多，图2是在图1基础上使用逆滤波去模糊，图3是在图1基础上使用维纳滤波去模糊；图4是添加了噪声和运动模糊，图5是再图4基础上逆滤波去模糊，图6是在图4维纳滤波去模糊。
注意：建议使用第一张图片进行代码验证，第一张图片效果更为明显。图片在下面自取：

参考代码：https://blog.csdn.net/bingbingxie1/article/details/79398601