【通信系统仿真】数字I/Q正交解调A/D转换的原理与仿真~中频采样接收机&Rader接收机&Shaw-Pohlig接收机

前言

I/Q解调技术广泛存在于无线通信中，其重要性毋庸置疑，然而传统的I/Q解调存在I/Q通道不匹配问题，导致Q通道存在I通道的“残余镜像”，严重破坏了正交性。近年来随着电子技术的发展，数字I/Q技术开始从理论走向实际，该技术可以克服模拟接收机通道的匹配限制。这些方法的特征包括在进行 A/D 转换之前采用模拟混频以及滤波方法将单一的实输入信号搬移到较低的中频。这样，同 RF 频段采样相比，会大大降低对 A/D 转换速度的耍求。此外，选择IF 频段会使对信号$exp(j{\omega }_{0}n)$的复数乘法运算变为相当简单的形式。其次，这类方法通过数字滤波和降采样联合处理来获得最终的输出，它仅包含所需原始频谱的边带信号，而且近似奈奎斯特采样率为每秒 $\beta$ 个复数样本¹。

仿真原理

发射部分

为了较为方便地获得带限信号，也方便后续进行匹配滤波（即脉冲压缩），仿真中使用线性扫频信号（也称为啁啾信号，LFM）作为发射端的基带信号，该信号$x_s[t]$的表达式为：
$$x_s[t]=e^{j\pi k{t}^2}$$
其中，k为线性调频因子，单位为Hz/s，表征信号频率的变化速率。
获得LFM复信号后，对其进行上变频，得到以载波频率为中心的带限I/Q调制信号$\widetilde{x_s}[n]$：
$$\widetilde{x_s}[n]=\mathrm{real}(x[t])?\cos (2\pi f_{0}t+?)?\mathrm{imag}(x[t])?\sin (2\pi f_{0}t+?)$$
其中，$f_0$为载波频率；$?$为载波初始相位。
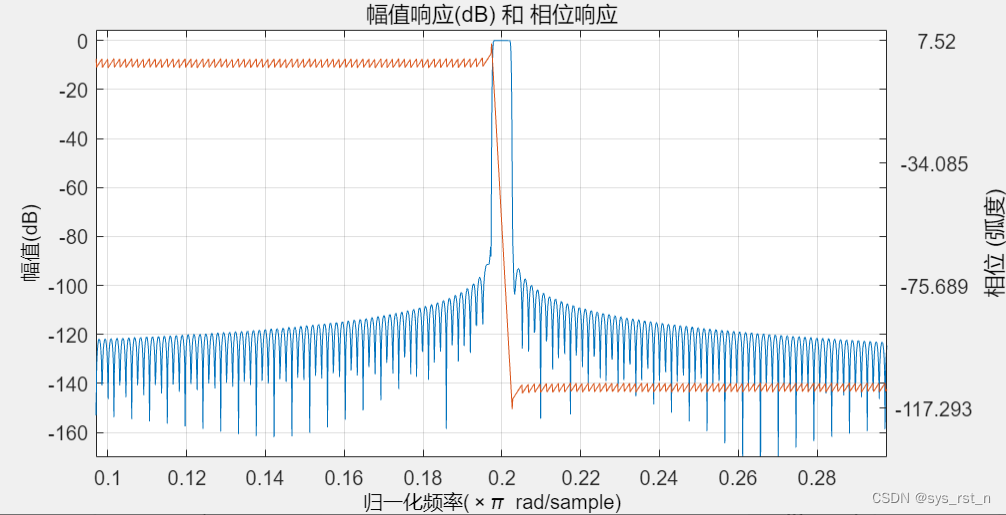
由于上变频后仍然有基带信号残留在频谱上，因此使用一个高通滤波器滤波后再发送，该滤波器的幅频和相频特征如下图：

接收机部分

天线谐振回路的模拟

为了模拟天线谐振回路，四种接收机的前面都加入了一个FIR带通滤波器，该滤波器的幅频曲线和相位相应如下图所示：

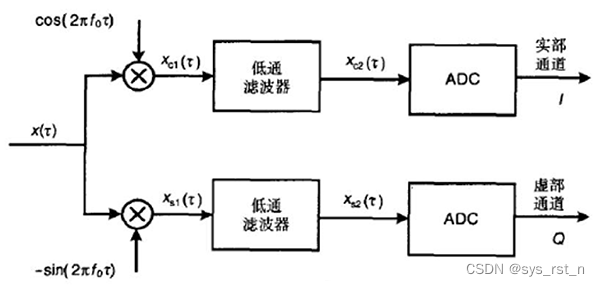
传统I/Q解调接收机及其失配问题

传统I/Q解调接收机原理如下图所示，原理已经烂大街，不再叙述。

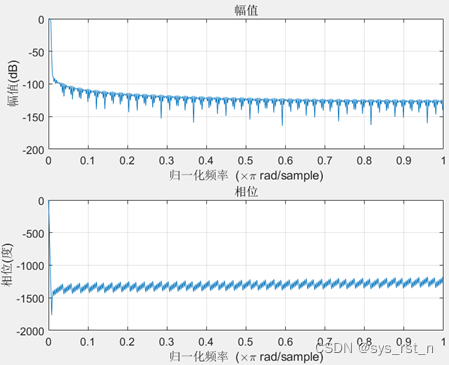
传统I/Q解调接收机的低通滤波器使用FIR低通滤波器实现，其幅频和相频响应曲线为：

传统I/Q解调接收机存在幅度失配误差、相位失配误差和直流偏置问题，其原理如下图所示。

可以推导得到输出x(t)为：
$$\begin{gathered} x(t)=A[\frac{\alpha +\beta }{2}{e}^{j\theta }+\frac{\alpha ?\beta }{2}{e}^{?j\theta }]+(\gamma +j\kappa ) \\ \alpha =1?j(1+\epsilon )\sin ? \\ \beta =(1+\epsilon )\cos ? \end{gathered}$$
其中，$(1+\epsilon )$为幅度失配因子；$?$为相位失配因子；$\gamma$和$\kappa$分别为Q通道和I通道的直流偏置。
当存在幅度或相位误差时，复信号x? 不仅包含所需的信号分量 $A{e}^{j\theta (t)}$(伴有轻微的幅度变化)，而且包含一个具有不同幅度，共轭相位函数的镜像分量，同时还包含一个复的直流偏置。镜像分量是由幅度和相位失配引起的误差，而直流分量则是单独通道中直流偏置的直接结果。

中频采样接收机

根据奈奎斯特采样定理，不失真采样率至少要为信号最高频率的两倍，才能实现无失真采样，如果按照该定理，采样率达到载频的两倍以上才能把信号采下来。实际上，当原信号为带通信号时，采样率只需要满足一定的条件（无需达到奈奎斯特采样率），就能无失真地将信号采样下来！
中频采样定理的原理如下图所示，左边为信号采样前的幅度谱，右边为采样后的频谱，采样率固定为400Hz，当带通信号的频带满足一定条件时，采样后的频谱与将该带通信号下变频后再采样（如下图最后一行和第一行所示）的频谱一致，不会发生频谱混叠！

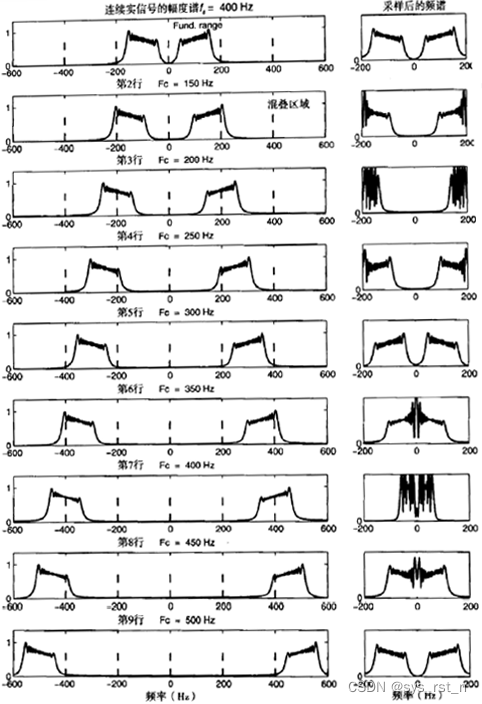
中频采样接收机正是基于上述中频采样定理设计而成，原理如下图所示，直接对信号进行低于中心频率的A/D采样，然后分别进行奇偶抽取，奇偶抽取后分别乘上一个-1的次方的序列实现频谱搬移，最后对Q通道进行FFT插值实现1/2的位移得到时间同步的IQ解调信号。相比于传统方法，该方法只有一个A/D模块，可有效解决多路A/D失配问题；AD采样率可低于中心频率实现数字解调，可解决模拟正交正弦信号相乘的相位失配和幅度失配问题；相比该与后面介绍的Rader接收机和shaw-Pohlig接收机无需滤波器，可减少处理延迟和资源。

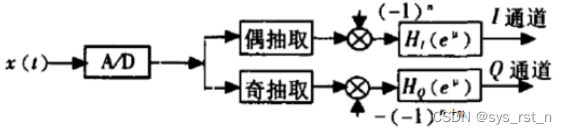
中频采样接收机的A/D模块采样率$f_s$的选取需要遵循以下规则：
$$f_s=\frac{4f_0}{2m+1},m\in Z^{+}$$
其中，$f_0$为信号的中心频率。需要注意奇抽取通道的-1序列生成与m有关，为$?(?1{)}^{n+m}$。
推导得到两个通道的表达式为：
$$\begin{gathered} I(n)=a(\frac{2n}{f_s})\cos (\phi (\frac{2n}{f_s})) \\ Q(n)=a(\frac{2n+1}{f_s})\sin (\phi (\frac{2n+1}{f_s})) \end{gathered}$$
其中，$a$和$\phi$分别为原始带通信号基带信号的幅度和相位。注意到Q通道比I通道时间上提前了$\frac{1}{2}$，因此对Q通道的数据做插值，由于时移量为1/2，这样的插值适合在频域进行，对Q通道数据做FFT变换后，乘上相移因子$e^{?j\pi k/N}$后，IFFT回时域并取实部，即可完成插值：
Q ( n ) = i f f t { f f t { Q ( n ) } ? f f t s h i f t { e ? j π k / N } } Q(n)=\mathrm {ifft}\{\mathrm {fft}\{Q(n)\}*\mathrm {fftshift}\{e^{-j\pi k/N}\}\} Q(n)=ifft{fft{Q(n)}?fftshift{e?jπk/N}}
其中$N$表示Q的样本点数量；$k$为从$?N/2$到$N/2$的$N$个等间隔采样点。

Rader接收机

Rader接收机由Rader(1984)²提出，假设RF信号的频谱为带通，信号带宽为$\beta$，它的结构如下图所示：

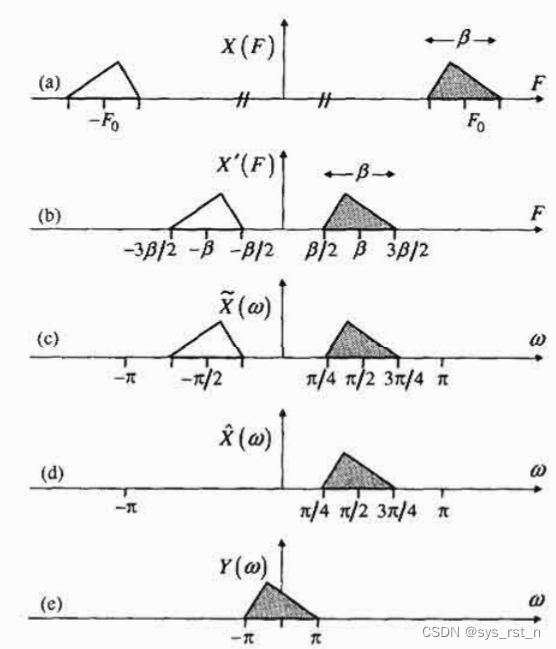
Rader接收机的每一步的频谱如下图所示，Rader接收机的处理步骤为：

1. 模拟频率搬移，将原始频谱将为$\beta$Hz的中频（频谱如下图b所示）；
2. 带通滤波器滤除由混频器产生的双倍频率项，频谱被限制在了$[\beta /2,3\beta /2]$之间（图c）；
3. A/D的采样率设置为$4\beta$Hz，采样后频谱如图d所示；
4. 正交解调的目的是选择带通信号的一个边带并将其转移到基带，这一步滤除掉信号的下边带（图d），所需要的滤波器的频率相应为：
   $$H(\omega )=?\begin{array}{cc}1& \frac{\pi }{4}<\omega <\frac{3\pi }{4}\\ & \\ 0& ?\frac{3\pi }{4}<\omega <?\frac{\pi }{4}\\ & \\ 不关心& 其它\end{array}$$
   在仿真实现上，直接使用希尔伯特变换取代，完成此步后，由于信号的频谱不是厄米的，信号的时域一定是复数的；
5. 最后一步为将信号下变频到基带（图e），该操作可以通过输出乘以序列$e^{?j\pi n/2}=(?j{)}^n$，并将每四个样本中的三个丢弃来实现。

仿真中，Rader接收机的带通滤波器的幅频和相频响应曲线如下图所示：

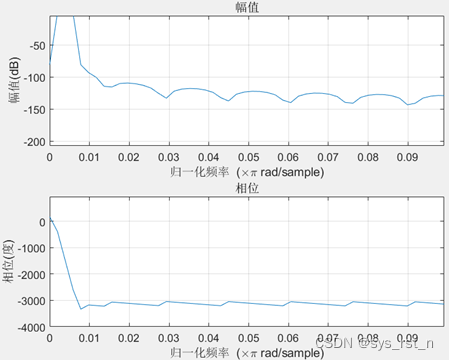
Rader接收机的数字I/Q结构将所需的模拟信号通道数由两个减少为一个，并使得正交振荡器以及增益，匹配问题变得毫无意义，另外A/D模块也减少到了一个。但是Rader接收机也有一些缺点，所需的A/D转换速率为传统I/Q解调的4倍，并且需要引入高速率的数字滤波器。

Shaw-Pohlig接收机

Shaw-Pohlig接收机由Shaw和Pohlig(1995)³所提出，结构如下图所示：

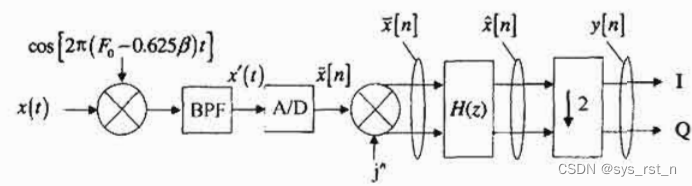
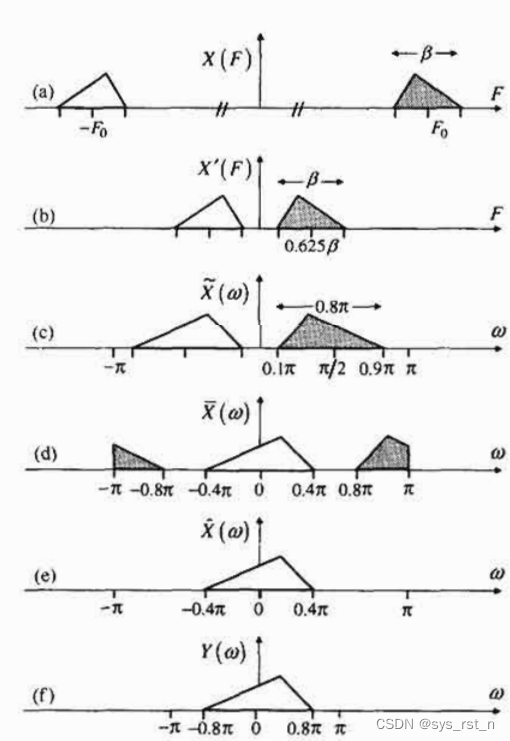
Shaw-Pohlig接收机每一步的频谱变化如下图所示，步骤为：

1. 采样模拟频率变换将信号的频谱搬移到比Rader所用频率更低的中频：$0.625\beta$，并进行带通滤波（图b）。
2. 设置A/D转换的采样率为$2.5\beta$，得到数字信号（图c）。
3. 利用信号$e^{j\pi n/2}=j^n$进行复调制，将下边带移动到基带，显然此时信号的时域为复信号（图d）。
4. 对复信号$\tilde{x}[n]$进行数字低通滤波，保留其$[?0.4\pi ,0.4\pi ]$范围内的部分（图e）。
5. 进行奇数抽取或偶数抽取，实现降采样率（图f）。

仿真中，Shaw-Pohlig接收机的模拟域带通滤波器的幅频和相频响应如下图所示：

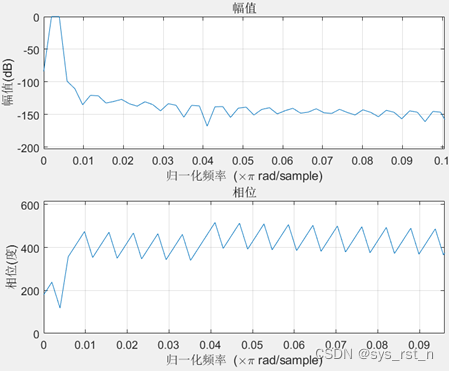
数字域的低通滤波器的幅频和相频响应如下图所示：

与Rader接收机相比，Shaw-Pohlig接收机的主要优点为A/D转换的采样率只需是信号带宽的2.5倍，而不是4倍，但也存在以下两个个缺点：

1. 较低的中频和采样率要求数字滤波器具有较陡峭的暂态导致滤波器阶数的增加和系统运算量的增加。
2. 最终采样率比基带信号的奈奎斯特采样率增加25%，而Rader的系统采样率与奈奎斯特采样率相同，采样率的增加使得整个数字系统处理中所需的最小计算量增加25%。
   需要注意的是，由于Shaw-Pohlig接收机采用的是信号的下边带，而其它接收机采用的是上边带，这回导致Shaw-Pohlig接收机的Q通道（即输出信号的虚部）与其它三种接收机符号相反。

接收机小结

接收机类型	A/D采样率/HZ	模拟滤波器个数	数字滤波器个数	数字复调制次数	主要缺点
传统I/Q解调	$1\beta$	2	0	0	存在I/Q通道失配问题
中频采样接收机	$\frac{4f_0}{2m+1}$	0	0	2	需要对Q通道时移1/2
Rader接收机	$4\beta$	1	2	1	A/D转换率为传统的4倍
Shaw-Pohlig接收机	$2.5\beta$	1	1	1	数字滤波器具有较陡峭的暂态

匹配滤波

为了评价接收机性能，对I/Q解调得到的复信号进行匹配滤波，实现脉冲压缩。匹配滤波器$x_{mf}[t]$的时域表达式为基带信号的共轭翻转：
$$x_{mf}[t]=x_s^{?}[?t]$$
在频域，匹配滤波器相当于对待匹配信号的幅频特性进行保留，对其相位进行取反。将I/Q解调得到的复信号与上述匹配滤波器做卷积，即可实现匹配滤波，将信号的能量集中在某一个时间点上。

仿真实现

仿真条件

1. 由于仿真的环境还是数字系统，因此对于接收机的模拟部分只能用高采样率进行逼近，在仿真中设计全局采样率$F_g$为50GHz。
2. 仿真使用的LFM信号带宽为100MHz，持续时间为30$\mu$s。
3. 载波频率为5GHz，初始相位为0和$\pi /6$分别测试。

这些条件都可以在代码中进行修改。

代码下载

GitHub：https://github.com/highskyno1/digital_IQ_AD

仿真结果

发射端

设置载波的初始相位为0，即为载波已同步状态，发射出去的LFM带限信号的频谱如下图所示，放大图中的一根”柱子“，可以看到频谱类似于一个矩形窗。

I/Q解调结果

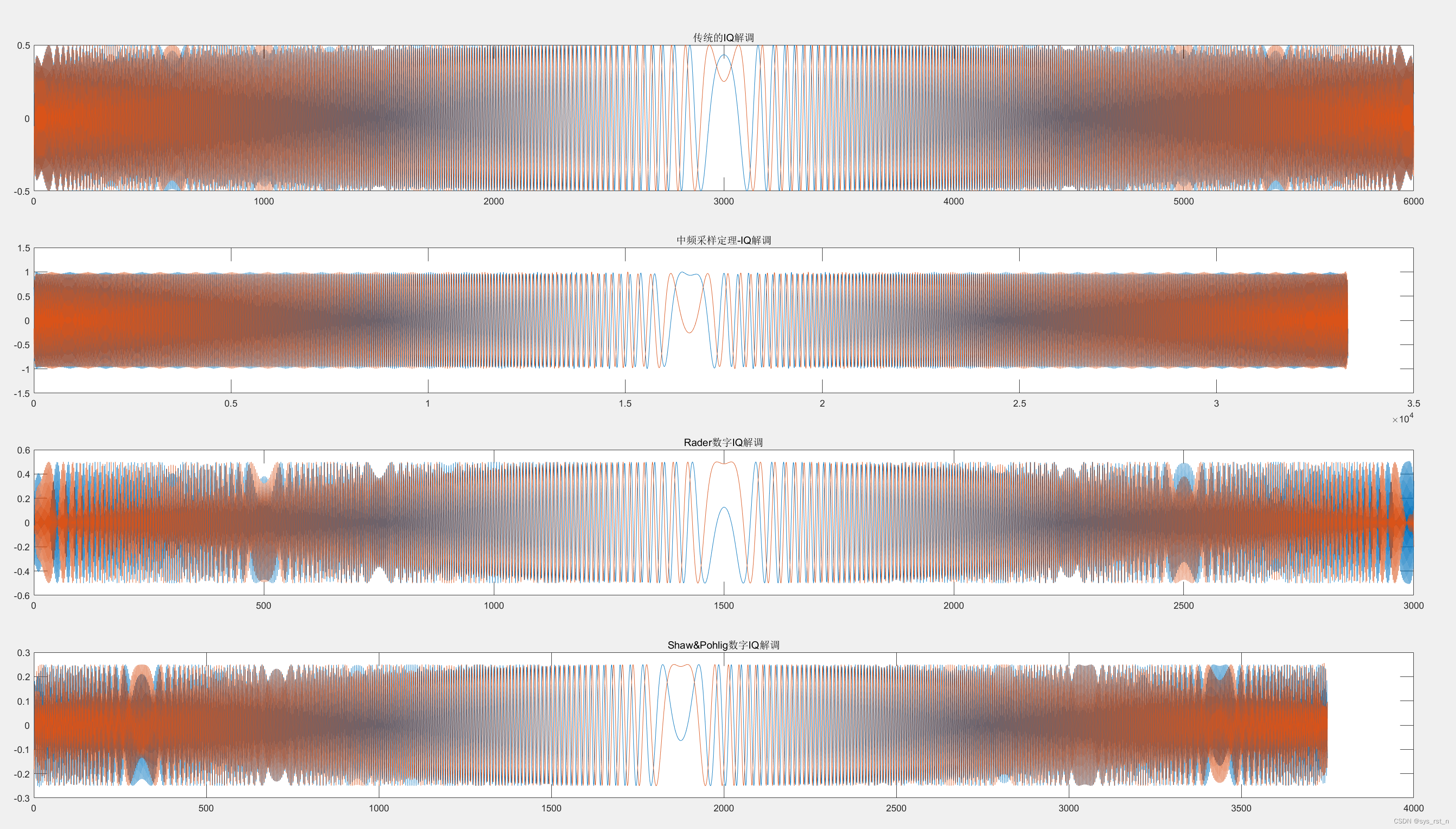
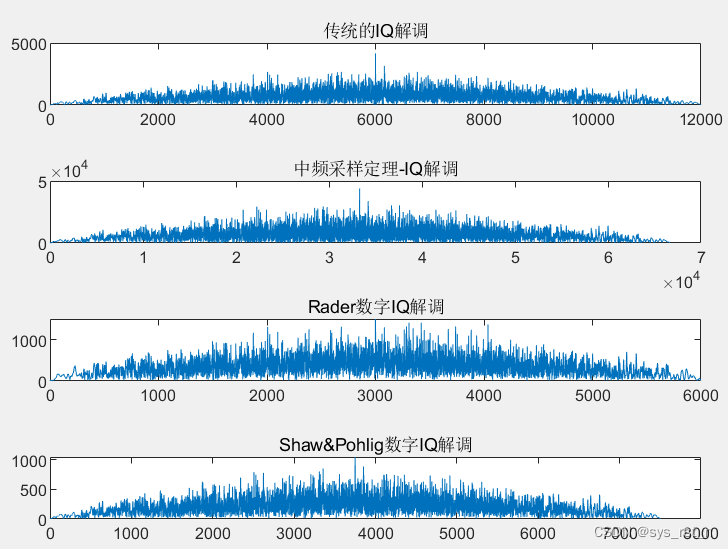
传统I/Q解调、中频采样接收机、Rader接收机和Shaw-Pohlig接收机的I/Q解调结果如下图所示：

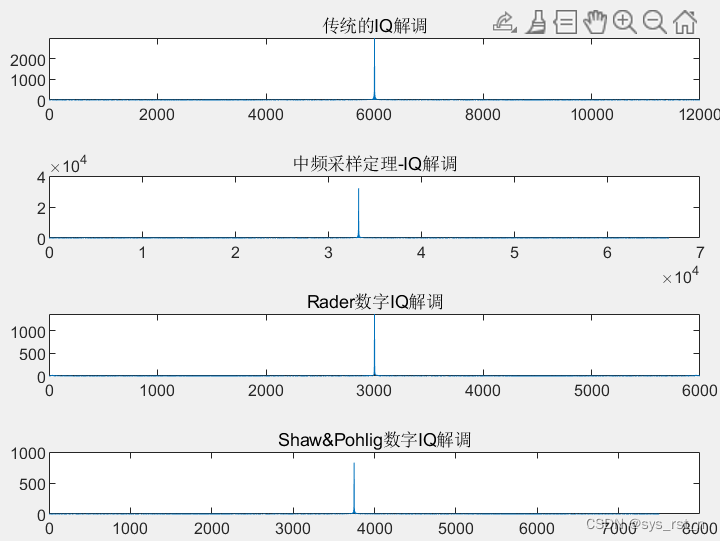
I/Q解调结果的频谱和相谱如下图所示，可见四种接收机接收结果的频谱和相谱比较接近。

匹配滤波结果

匹配滤波结果如下图所示，可见四种接收机得到的I/Q解调信号都可以实现不错的脉冲压缩效果。

为了测试系统能完成脉冲压缩的最小信噪比，对发射信号添加白噪声，发现在信噪比为-47dB时，系统的输出刚好能满足脉冲压缩，结果如下图所示，信噪比再小时，脉冲压缩失败。

后语

自从读了研究生，好像有两年多没有写过CSDN了，因为硕士阶段接触的项目等都跟通信关系不大，没有啥新的idea或有趣的东西写博文，在搞的工作都写成小论文投出去了。现在，在一个新的与通信相关的领域读上博士了，在学习阶段的一些有趣的仿真又可以写成博文记录一下。

看到这了，不^点个赞再走吗？

附录代码

main.m

%{
    仿真中频采样定理
    case1：发射端用了IQ调制
    2023/12/23 11:37
%}
close all;
%% 仿真全局参数
Bandwidth = 1e8;    % 脉冲带宽
T = 30e-6;          % 脉冲持续时间 s
Center_frq = 5e9;   % 中心频率
Fg = 50e9;          % 仿真全局采样率
phase_id = 0;       % 发射端与接收端的相位差，0表示本振同步
lfm_sig_snr = +inf; % 接收端接收到的信号的信噪比

%% LFM信号发生
K = Bandwidth / T;                  % 线性调频因子
N = Fg * T;                         % 采样点数
t_axis = linspace(-T/2,T/2,N);      % 采样时间点
lfm_sig = exp(1i*pi*K.*(t_axis.^2));% 采样得到的信号
% 上变频(IQ调制)
lfm_sig_up = real(lfm_sig) .* cos(2*pi*Center_frq.*t_axis + phase_id);
lfm_sig_up = lfm_sig_up + imag(lfm_sig) .* (-sin(2*pi*Center_frq.*t_axis + phase_id));
% 由于信号还有基带残留，滤除
HP = up_freq_HP(Fg,1.5e8,1e9);
HP = HP.Numerator;
lfm_sig_up = conv(lfm_sig_up,HP,'same');
% 查看发射信号的频谱
fft_x = linspace(-Fg/2,Fg/2,N);
figure('Name','发射信号的频谱');
plot(fft_x,fftshift(abs(fft(lfm_sig_up))));
% 加噪
lfm_sig_up = awgn(lfm_sig_up,lfm_sig_snr);

%% 所有接收机天线的带通滤波
BP_rec = BP_filter(Fg,Center_frq-Bandwidth/1.5,Center_frq-Bandwidth/2,...
    Center_frq+Bandwidth/2,Center_frq+Bandwidth/1.5);
lfm_sig_up = conv(lfm_sig_up,BP_rec.Numerator,'same');

%% 模拟传统IQ解调（零中频模式）
% I通道混频序列
I_df = cos(2*pi*Center_frq.*t_axis);
% Q通道混频系列
Q_df = -sin(2*pi*Center_frq.*t_axis);
% 低通滤波器
LP = Lp_filter(Fg,Bandwidth,Bandwidth*2);
% IQ通道数据
I_ch = conv(lfm_sig_up .* I_df,LP.Numerator,'same');
Q_ch = conv(lfm_sig_up .* Q_df,LP.Numerator,'same');
% 利用插值模拟A/D抽样
% 计算采样率
fs_iq = Bandwidth * 2;
% 计算采样点数
N_iq = floor(fs_iq * T);
t_axis_iq = linspace(-T/2,T/2,N_iq);
% 采样
sample_i = interp1(t_axis,I_ch,t_axis_iq,"linear","extrap");
sample_q = interp1(t_axis,Q_ch,t_axis_iq,"linear","extrap");
% 得到复信号
AD_iq_res = sample_i + 1i .* sample_q;
% 匹配滤波
mf_sig = conj(flip(exp(1i.*pi*K.*(t_axis_iq.^2))));   % 匹配滤波器
ip_mf_sig = conv(mf_sig,AD_iq_res);             % 匹配滤波结果

%% 模拟中频采样定理
% 计算采样率
m = 4;
fs_m = 4 * Center_frq / (2*m+1);
% A/D采样
Nm = floor(fs_m * T);
t_axis_m = linspace(-T/2,T/2,Nm);
sample_m = interp1(t_axis,lfm_sig_up,t_axis_m,"linear","extrap");
% 奇偶抽取
sample_even = sample_m(1:2:Nm);
sample_odd = sample_m(2:2:Nm);
% 相乘
sample_even = sample_even .* ((-1).^(0:length(sample_even)-1));
sample_odd = sample_odd .* (-(-1).^((0:length(sample_odd)-1)+m));
% Q通道相移
len = length(sample_odd);
sample_odd_fft = fft(sample_odd) .* fftshift(exp(-1i*pi/len.*linspace(-len/2,len/2,len)));
sample_odd = real(ifft(sample_odd_fft));
% 得到复信号
AD_m_res = sample_even + 1i.*sample_odd;
% 匹配滤波
% 由于进行了奇偶抽取，等效采样率降低了
t_axis_mf = linspace(-T/2,T/2,Nm/2);
mf_sig = conj(flip(exp(1i.*pi*K.*(t_axis_mf.^2))));   % 匹配滤波器
m_mf_sig = conv(mf_sig,AD_m_res);               % 匹配滤波结果

%% 模拟Rader法
% 下变频
Rader_dp = cos(2*pi*(Center_frq-Bandwidth).*t_axis);
reder_sig = lfm_sig_up .* Rader_dp;
% 带通滤波
bp_lowp = 0.5 * Bandwidth;      % 通带下限
bp_upp = 1.5 * Bandwidth;       % 通带上限
bp_interim = 0.1 * Bandwidth;   % 过度带宽
B_raderP = BP_filter(Fg,bp_lowp-bp_interim,bp_lowp,bp_upp,bp_upp+bp_interim);
reder_sig = conv(reder_sig,B_raderP.Numerator,'same');
% 模拟A/D采样(采样率为4beita)
fs_rad = 4 * Bandwidth;
N_rad = floor(fs_rad * T);
t_axis_rader = linspace(-T/2,T/2,N_rad);
sample_rader = interp1(t_axis,reder_sig,t_axis_rader,"linear","extrap");
% 通过复数系统，抹掉负半部分的频率，等效于希尔伯特变换
sample_rader = hilbert(sample_rader);
% 频谱搬移，乘上(-j)^n
sample_rader = sample_rader .* (-1i).^(0:N_rad-1);
% 1/4降采样
sample_rader = sample_rader(1:4:N_rad);
% 匹配滤波
% 进行了1/4降采样，匹配模板也要
t_axis_rader_mf = linspace(-T/2,T/2,N_rad/4);
mf_sig = conj(flip(exp(1i.*pi*K.*(t_axis_rader_mf.^2))));   % 匹配滤波器
rader_mf_sig = conv(mf_sig,sample_rader);                   % 匹配滤波结果

%% 模拟Shaw&Pohlig法
% 下变频
sp_dp = cos(2*pi*(Center_frq-0.625*Bandwidth).*t_axis);
sp_sig = lfm_sig_up .* sp_dp;
% 带通滤波
bp_lowp = 0.125 * Bandwidth;    % 通带下限
bp_upp = 1.625 * Bandwidth;     % 通带上限
bp_interim = 0.1 * Bandwidth;   % 过渡带宽
BP_sp = BP_filter(Fg,bp_lowp-bp_interim,bp_lowp,bp_upp,bp_upp+bp_interim);
sp_dp = conv(sp_sig,BP_sp.Numerator,'same');
% AD采样
fs_sp = 2.5 * Bandwidth;
N_sp = floor(fs_sp * T);
t_sp_axis = linspace(-T/2,T/2,N_sp);
sample_sp = interp1(t_axis,sp_dp,t_sp_axis,"linear","extrap");
% 复调制，乘上j^n
sample_sp = sample_sp .* (1i).^(0:N_sp-1);
% 低通滤波
LP_sp = Lp_filter(1,0.2,0.25);
sample_sp = conv(sample_sp,LP_sp.Numerator,'same');
% 1/2降采样
sample_sp = sample_sp(1:2:N_sp);
% 匹配滤波
% 进行了1/2降采样，匹配模板也要
t_sp_axis_mf = linspace(-T/2,T/2,N_sp/2);
% !!由于Shaw&Pohlig接收机得到的虚部已取反，匹配模板不需要取共轭
mf_sig = flip(exp(1i.*pi*K.*(t_sp_axis_mf.^2)));   % 匹配滤波器
sp_mf_sig = conv(mf_sig,sample_sp);          % 匹配滤波结果


%% 画图
% 采样结果
figure('Name','采样结果');
subplot(411);
plot(real(AD_iq_res));
hold on
plot(imag(AD_iq_res));
title('传统的IQ解调');
subplot(412);
plot(real(AD_m_res));
hold on
plot(imag(AD_m_res));
title('中频采样定理-IQ解调');
subplot(413);
plot(real(sample_rader));
hold on
plot(imag(sample_rader));
title('Rader数字IQ解调');
subplot(414);
plot(real(sample_sp));
hold on
plot(imag(sample_sp));
title('Shaw&Pohlig数字IQ解调');

% 采样结果(abs)
figure('Name','采样结果(abs)');
title('采样结果')
subplot(411);
plot(abs(AD_iq_res));
title('传统的IQ解调');
subplot(412);
plot(abs(AD_m_res));
title('中频采样定理-IQ解调');
subplot(413);
plot(abs(sample_rader));
title('Rader数字IQ解调');
subplot(414);
plot(abs(sample_sp));
title('Shaw&Pohlig数字IQ解调');

% 采样结果的频域比较
figure('Name','采样结果的频域');
subplot(411);
foo_fft = fft(AD_iq_res);
x_fft = linspace(-1,1,length(foo_fft));
fft_abs = fftshift(abs(foo_fft));
fft_phase = fftshift(phase(foo_fft));
yyaxis left
plot(x_fft,fft_abs);
yyaxis right
plot(x_fft,fft_phase);
title('传统的IQ解调');
subplot(412);
foo_fft = fft(AD_m_res);
x_fft = linspace(-1,1,length(foo_fft));
fft_abs = fftshift(abs(foo_fft));
fft_phase = fftshift(phase(foo_fft));
yyaxis left
plot(x_fft,fft_abs);
yyaxis right
plot(x_fft,fft_phase);
title('中频采样定理-IQ解调');
subplot(413);
foo_fft = fft(sample_rader);
x_fft = linspace(-1,1,length(foo_fft));
fft_abs = fftshift(abs(foo_fft));
fft_phase = fftshift(phase(foo_fft));
yyaxis left
plot(x_fft,fft_abs);
yyaxis right
plot(x_fft,fft_phase);
title('Rader数字IQ解调');
subplot(414);
foo_fft = fft(sample_sp);
x_fft = linspace(-1,1,length(foo_fft));
fft_abs = fftshift(abs(foo_fft));
fft_phase = fftshift(phase(foo_fft));
yyaxis left
plot(x_fft,fft_abs);
yyaxis right
plot(x_fft,fft_phase);
title('Shaw&Pohlig数字IQ解调');

% 匹配滤波结果
figure('Name','匹配滤波结果');
subplot(411);
plot(real(ip_mf_sig));
hold on
plot(imag(ip_mf_sig));
title('传统的IQ解调');
subplot(412);
plot(real(m_mf_sig));
hold on
plot(imag(m_mf_sig));
title('中频采样定理-IQ解调');
subplot(413);
plot(real(rader_mf_sig));
hold on
plot(imag(rader_mf_sig));
title('Rader数字IQ解调');
subplot(414);
plot(real(sp_mf_sig));
hold on
plot(imag(sp_mf_sig));
title('Shaw&Pohlig数字IQ解调');

% 匹配滤波结果(abs)
figure('Name','匹配滤波结果(abs)');
subplot(411);
plot(abs(ip_mf_sig));
title('传统的IQ解调');
subplot(412);
plot(abs(m_mf_sig));
title('中频采样定理-IQ解调');
subplot(413);
plot(abs(rader_mf_sig));
title('Rader数字IQ解调');
subplot(414);
plot(abs(sp_mf_sig));
title('Shaw&Pohlig数字IQ解调');

---

1. Richards, M. A. (2005). Fundamentals of radar signal processing (Vol. 1). New York: Mcgraw-hill. ??

2. Rader, C. M. (1984). A simple method for sampling in-phase and quadrature components. IEEE Transactions on Aerospace and Electronic Systems, (6), 821-824. ??

3. Shaw, G. A., & Pohlig, S. C. (1995). I/Q baseband demodulation in the RASSP SAR benchmark. Lincoln Laboratory, Massachusetts Institute of Technology. ??