真题案例（三）：力扣真题训练

力扣真题训练

在看真题前，我们再重复一遍通用的解题方法论，它可以分为以下 4 个步骤：

1. 复杂度分析。估算问题中复杂度的上限和下限。

2. 定位问题。根据问题类型，确定采用何种算法思维。

3. 数据操作分析。根据增、删、查和数据顺序关系去选择合适的数据结构，利用空间换取时间。

4. 编码实现。

例题 1：删除排序数组中的重复项

【题目】 给定一个排序数组，你需要在原地删除重复出现的元素，使得每个元素只出现一次，返回移除后的数组和新的长度，你不需要考虑数组中超出新长度后面的元素。

要求：空间复杂度为 O(1)，即不要使用额外的数组空间。

例如，给定数组 nums = [1,1,2]，函数应该返回新的长度 2，并且原数组 nums 的前两个元素被修改为 1, 2。又如，给定 nums = [0,0,1,1,1,2,2,3,3,4]，函数应该返回新的长度 5，并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。

【解析】 这个题目比较简单，应该是送分题。不过，面试过程中的送分题也是送命题。这是因为，如果送分题没有拿下，就会显得非常说不过去。

我们先来看一下复杂度。这里并没有限定时间复杂度，仅仅是要求了空间上不能定义新的数组。

然后我们来定位问题。显然这是一个数据去重的问题。

按照解题步骤，接下来我们需要做数据操作分析。 在一个去重问题中，每次遍历的新的数据，都需要与已有的不重复数据进行对比。这时候，就需要查找了。整体来看，遍历嵌套查找，就是 O(n2) 的复杂度。如果要降低时间复杂度，那么可以在查找上入手，比如使用哈希表。不过很可惜，使用了哈希表之后，空间复杂度就是 O(n)。幸运的是，原数组是有序的，这就可以让查找的动作非常简单了。

因此，解决方案上就是，一次循环嵌套查找完成。查找不可使用哈希表，但由于数组有序，时间复杂度是 O(1)。因此整体的时间复杂度就是 O(n)。

我们来看一下具体方案。既然是一次循环，那么就需要一个 for 循环对整个数组进行遍历。每轮遍历的动作是查找 nums[i] 是否已经出现过。因为数组有序，因此只需要去对比 nums[i] 和当前去重数组的最大值是否相等即可。我们用一个 temp 变量保存去重数组的最大值。

如果二者不等，则说明是一个新的数据。我们就需要把这个新数据放到去重数组的最后，并且修改 temp 变量的值，再修改当前去重数组的长度变量 len。直到遍历完，就得到了结果。

最后，我们按照上面的思路进行编码开发，代码如下：

public static void main(String[] args) {
    int[] nums = {0,0,1,1,1,2,2,3,3,4};
    int temp = nums[0];
    int len = 1;
    for (int i = 1; i < nums.length; i++) {
        if (nums[i] != temp) {
            nums[len] = nums[i];
            temp = nums[i];
            len++;
        }
    }
    System.out.println(len);
    for (int i = 0; i < len; i++) {
        System.out.println(nums[i]);
    }
}

我们对代码进行解读。 在这段代码中，第 3～4 行进行了初始化，得到的 temp 变量是数组第一个元素，len 变量为 1。

接着进入 for 循环。如果当前元素与去重的最大值不等（第 6 行），则新元素放入去重数组中（第 7 行），并且更新去重数组的最大值（第 8 行），再让去重数组的长度加 1（第 9 行）。最后得到结果后，再打印出来，第 12～15 行。

例题 2：查找两个有序数组合并后的中位数

【题目】 两个有序数组查找合并之后的中位数。给定两个大小为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出这两个正序数组合在一起之后的中位数，并且要求算法的时间复杂度为 O(log(m + n))。

你可以假设 nums1 和 nums2 不会同时为空，所有的数字全都不相等。还可以再假设，如果数字个数为偶数个，中位数就是中间偏左的那个元素。

例如：nums1 = [1, 3, 5, 7, 9]

nums2 = [2, 4, 8, 12]

输出 5。

【解析】 这个题目是我个人非常喜欢的，原因是，它所有的解法和思路，都隐含在了题目的描述中。如果你具备很强的分析和解决问题的能力，那么一定可以找到最优解法。

我们先看一下复杂度的分析。这里的 nums1 和 nums2 都是有序的，这让我们第一时间就想到了归并排序。方法很简单，我们把两个数组合并，就得到了合在一起后的有序数组。这个动作的时间复杂度是 O(m+n)。接着，我们从数组中就可以直接取出中位数了。很可惜，这并不满足题目的时间复杂度 O(log(m + n)) 的要求。

接着，我们来看一下这个问题的定位。题目中有一个关键字，那就是“找出”。很显然，我们要找的目标就藏在 nums1 或 nums2 中。这明显就是一个查找问题。而在查找问题中，我们学过的知识是分治法下的二分查找。

回想一下，二分查找适用的重要条件就是，原数组有序。恰好，在这个问题中 nums1 和 nums2 分别都是有序的。而且二分查找的时间复杂度是 O(logn)，这和题目中给出的时间复杂度 O(log(m + n)) 的要求也是不谋而合。因此，经过分析，我们可以大胆猜测，此题极有可能要用到二分查找。

我们再来看一下数据结构方面。如果要用二分查找，就需要用到若干个指针，去约束查找范围。除此以外，并不需要去定义复杂的数据结构。也就是说，空间复杂度是 O(1) 。

好了，接下来，我们就来看一下二分查找如何能解决这个问题。二分查找需要一个分裂点，去把原来的大问题，拆分成两个部分，并在其中一部分继续执行二分查找。既然是查找中位数，我们不妨先试试以中位数作为切分点，看看会产生什么结果。如下图所示：

经过切分后，两个数组分别被拆分为 3 个部分，合在一起是 6 个部分。二分查找的思路是，需要从这 6 个部分中，剔除掉一些，让查找的范围缩小。那么，我们来思考一个问题，在这 6 个部分中，目标中位数一定不会发生在哪几个部分呢？

中位数有一个重要的特质，那就是比中位数小的数字个数，和比中位数大的数字个数，是相等的。围绕这个性质来看，中位数就一定不会发生在 C 和 D 的区间。

如果中位数在 C 部分，那么在 nums1 中，比中位数小的数字就会更多一些。因为 4 < 5（nums2 的中位数小于 nums1 的中位数），所以在 nums2 中，比中位数小的数字也会更多一些（最不济也就是一样多）。因此，整体来看，中位数不可能在 C 部分。同理，中位数也不会发生在 D 部分。

接下来，我们就可以在查找范围内，剔除掉 C 部分（永远比中位数大的数字）和 D 部分（永远比中位数小的数字），这样我们就成功地完成了一次二分动作，缩小了查找范围。然而这样并没结束。剔除掉了 C 和 D 之后，中位数有可能发生改变。这是因为，C 部分的数字个数和 D 部分数字的个数是不相等的。剔除不相等数量的“小数”和“大数”后，会造成中位数的改变。

为了解决这个问题，我们需要对剔除的策略进行修改。一个可行的方法是，如果 C 部分数字更少为 p 个，则剔除 C 部分；并只剔除 D 部分中的 p 个数字。这样就能保证，经过一次二分后，剔除之后的数组的中位数不变。

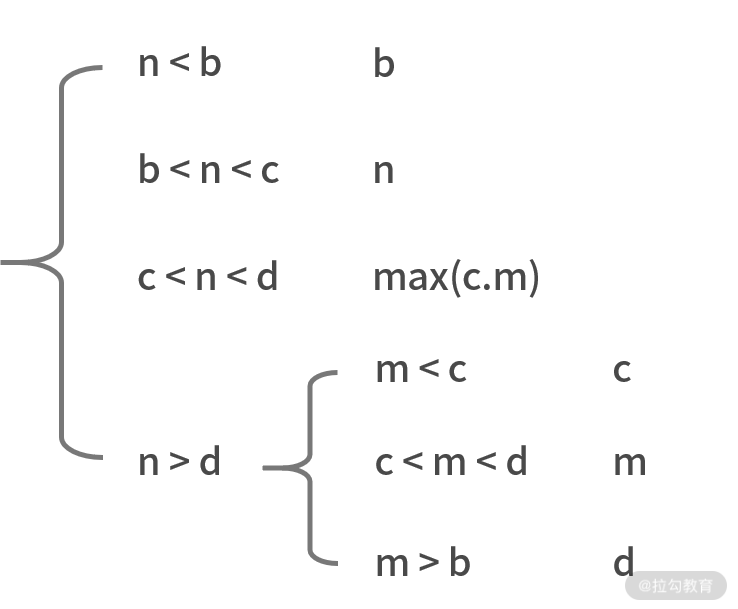
应该剔除 C 部分和 D 部分。但 D 部分更少，因此剔除 D 和 C 中的 9。

二分查找还需要考虑终止条件。对于这个题目，终止条件必然是某个数组小到无法继续二分的时候。这是因为，每次二分剔除掉的是更少的那个部分。因此，在终止条件中，查找范围应该是一个大数组和一个只有 1～2 个元素的小数组。这样就需要根据大数组的奇偶性和小数组的数量，拆开 4 个可能性：

可能性一：nums1 奇数个，nums2 只有 1 个元素。例如，nums1 = [a, b, c, d, e]，nums2 = [m]。此时，有以下 3 种可能性：

1. 如果 m < b，则结果为 b；

2. 如果 b < m < c，则结果为 m；

3. 如果 m > c，则结果为 c。

这 3 个情况，可以利用 "A?B:C" 合并为一个表达式，即 m < b ? b : (m < c ? m : c)。

可能性二：nums1 偶数个，nums2 只有 1 个元素。例如，nums1 = [a, b, c, d, e, f]，nums2 = [m]。此时，有以下 3 种可能性：

1. 如果 m < c，则结果为 c；

2. 如果 c < m < d，则结果为 m；

3. 如果m > d，则结果为 d。

这 3 个情况，可以利用"A?B:C"合并为一个表达式，即 m < c ? c : (m < d? m : d)。

可能性三：nums1 奇数个，nums2 有 2 个元素。例如，nums1 = [a, b, c, d, e]，nums2 = [m,n]。此时，有以下 6 种可能性：

1. 如果 n < b，则结果为 b；

2. 如果 b < n < c，则结果为 n；

3. 如果 c < n < d，则结果为 max(c,m)；

4. 如果 n > d，m < c，则结果为 c；

5. 如果 n > d，c < m < d，则结果为 m；

6. 如果 n > d，m > d，则结果为 d。

其中，4～6 可以合并为，如果 n > d，则返回 m < c ? c : (m < d ? m : d)。

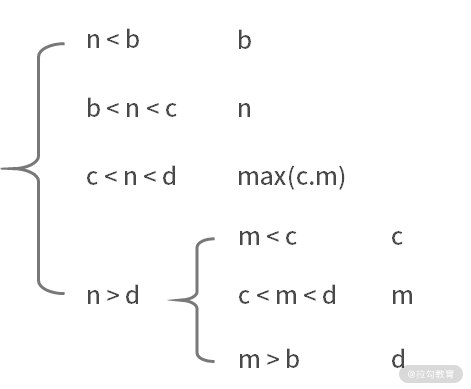
可能性四：nums1 偶数个，nums2 有 2 个元素。例如，nums1 = [a, b, c, d, e, f]，nums2 = [m,n]。此时，有以下 6 种可能性：

1. 如果 n < b，则结果为 b；

2. 如果 b < n < c，则结果为 n；

3. 如果 c < n < d，则结果为 max(c,m)；

4. 如果 n > d，m < c，则结果为 c；

5. 如果 n > d，c < m < d，则结果为 m；

6. 如果 n > d，m > d，则结果为 d。与可能性 3 完全一致。

不难发现，终止条件都是 if 和 else 的判断，虽然逻辑有点复杂，但时间复杂度是 O(1) 。为了简便，我们可以假定，nums1 的数字数量永远是不少于 nums2 的数字数量。

因此，我们可以编写如下的代码：

public static void main(String[] args) {  
    int[] nums1 = {1,2,3,4,5};    
    int[] nums2 = {6,7,8};    
    int median = getMedian(nums1,0, nums1.length-1, nums2, 0, nums2.length-1);    
    System.out.println(median); }

public static int getMedian(int[] a, int begina, int enda, int[] b, int beginb, int endb ) {
    if (enda - begina == 0) {
    return a[begina] > b[beginb] ? b[beginb] : a[begina];
    }
    if (enda - begina == 1){
    if (a[begina] < b[beginb]) {
    return b[beginb] > a[enda] ? a[enda] : b[beginb];
    }
    else {
    return a[begina] < b[endb] ? a[begina] : b[endb];
    }
    }
    if (endb-beginb < 2) {
    if ((endb - beginb == 0) && (enda - begina)%2 == 0) {
    int m = b[beginb];
    int bb = a[(enda + begina)/2 - 1];
    int c = a[(enda + begina)/2];
    return (m < bb) ? bb : (m < c ? m : c);
    }
    else if ((endb - beginb == 0) && (enda - begina)%2 != 0) {
    int m = b[beginb];
    int c = a[(enda + begina)/2];
    int d = a[(enda + begina)/2 + 1];
    return m < c ? c : (m < d ? m : d);
    }
    else {
    int m = b[beginb];
    int n = b[endb];
    int bb = a[(enda + begina)/2 - 1];
    int c = a[(enda + begina)/2];
    int d = a[(enda + begina)/2 + 1];
    if (n<bb) {
    return bb;
    }
    else if (n>bb && n < c) {
    return n;
    }
    else if (n > c && n < d) {
    return m > c ? m : c;
    }
    else {
    return m < c ? c : (m<d ? m : d);
    }
    }
    }
    else {
    int mida = (enda + begina)/2;
    int midb = (endb + beginb)/2;
    if (a[mida] < b[midb]) {
    int step = endb - midb;
    return getMedian(a,begina + step, enda, b, beginb, endb - step);
    }
    else {
    int step = midb - beginb;
    return getMedian(a,begina,enda - step, b, beginb+ step, endb );
    }
    }

我们对代码进行解读。在第 1～6 行是主函数，进入 getMedian() 中，入参分别是 nums1 数组，nums1 数组搜索范围的起止索引；nums2 数组，nums2 数组搜索范围的起止索引。并进入第 8 行的函数中。

在 getMedian() 函数中，第 53～64 行是二分策略，第 9～52 行是终止条件。我们先看二分部分。通过第 56 行，判断 a 和 b 的中位数的大小关系，决策剔除哪个部分。并在第 58 行和 62 行，递归地执行二分动作缩小范围。

终止条件的第一种可能性在第 21～26 行，第二种可能性在 27～32 行，第三种和第四种可能性完全一致，在 33～52 行。另外，在 9～19 行中处理了两个特殊情况，分别是第 9～11 行，处理了两个数组都只剩 1 个元素的情况；第 12～19 行，处理了两个数组都只剩 2 个元素的情况。

这段代码的逻辑并不复杂，但写起来还是有很多情况需要考虑的。希望你能认真阅读。

总结

综合来看，力扣的题目还是比较受到行业的认可的。一方面是它的题库内题目数量多，另一方面是很多人会在上面提交相同题目的不同解法和答案。但对初学者来说，它还是有一些不友好的。这主要在于，它的定位只是题库，并不能提供完整的解决问题的思维逻辑和方法论。

本课时，虽然我们只是举了两个例题，但其背后解题的思考方法是通用的。建议你能围绕本课程学到的解题方法，利用空闲时间去把力扣热门的题目都练习一遍。

练习题

最后，我们再给出一道练习题。给定一个链表，删除链表的倒数第 n 个节点。

例如，给定一个链表: 1 -> 2 -> 3 -> 4 -> 5, 和 n = 2。当删除了倒数第二个节点后，链表变为 1 -> 2 -> 3 -> 5。

你可以假设，给定的 n 是有效的。额外要求就是，要在一趟扫描中实现，即时间复杂度是 O(n)。这里给你一个提示，可以采用快慢指针的方法。

---