Wheel-INS 源码解读
上一篇文章分享了论文“基于车轮安装MEMS IMU的航迹推算算法研究”。
基于车轮安装MEMS IMU的航迹推算算法研究
纸上得来终觉浅,绝知此事要躬行。看再多的论文,不用代码实现一下,看看效果总觉得不得劲,刚好论文作者写有相关源码并提供了数据集,所以我们详细解读下,尽量做到公式与代码对应起来,完整呈现,真正做到看完就会的效果,哈哈。有问题请批评指正~
阅前知悉:
源码与论文的主要区别:
1.状态向量为pvacur(pos、vel、att(q, R, euler), acc/gyro bias acc/gyro scale),没有考虑里程计比例因子误差和杠臂误差;
2.没有利用载体运动约束:零速更新和零速航向更新ZUPT/ZIHR。
源码地址:https://github.com/i2Nav-WHU/Wheel-INS
配套源码程序支持ubuntu/window,为了省去配置麻烦,这里只解读ubuntu环境下版本。
程序结构:

可以看到Wheel-INS包括:配置文件config,并提供配置文件相对应的数据dataset,第三方依赖库ThirdParty,常有工具文件夹utils、如画图,源码部分在src中。文件结构简单、清晰。
程序入口main
主要分为几个部分:导入相应yaml配置文件,读取数据,newImuProcess,存储结果。
一、导入相应yaml配置文件
文件导入通过yaml文件格式导入,源码中有点值得借鉴的是,导入yaml文件时,通过try catch做异常处理。这样做很友好,因为很多同学跑一些源码工程莫名跑不起来,有一部分就是yaml部分参数格式设置不对的,有这个异常跑出就可以很容易定位问题做在了。如下:
YAML::Node config;
try {
config = YAML::LoadFile(argv[1]);
} catch (YAML::Exception &exception) {
std::cout << "Failed to read configuration file: " << exception.what()
<< std::endl;
return -1;
}
从上面程序片段可以看出,如果运行代码时,如果第二个参数没有yaml文件就直接跑出异常,退出程序。
接下来重点看下loadConfig函数
inline bool loadConfig(YAML::Node &config, Paras ¶s) {
std::vector<double> initposstd_vec, initvelstd_vec, initattstd_vec;
try {
initposstd_vec = config["initposstd"].as<std::vector<double>>();
initvelstd_vec = config["initvelstd"].as<std::vector<double>>();
initattstd_vec = config["initattstd"].as<std::vector<double>>();
} catch (YAML::Exception &exception) {
std::cout << "Failed when loading configuration. Please check initial std "
"of position, velocity, and attitude!"
<< std::endl;
return false;
}
for (int i = 0; i < 3; i++) {
paras.initstate_std.pos[i] = initposstd_vec[i];
paras.initstate_std.vel[i] = initvelstd_vec[i];
paras.initstate_std.euler[i] = initattstd_vec[i] * D2R;
}
double arw, vrw, gbstd, abstd, gsstd, asstd;
try {
arw = config["imunoise"]["arw"].as<double>();
vrw = config["imunoise"]["vrw"].as<double>();
gbstd = config["imunoise"]["gbstd"].as<double>();
abstd = config["imunoise"]["abstd"].as<double>();
gsstd = config["imunoise"]["gsstd"].as<double>();
asstd = config["imunoise"]["asstd"].as<double>();
paras.imunoise.corr_time = config["imunoise"]["corrtime"].as<double>();
} catch (YAML::Exception &exception) {
std::cout << "Failed when loading configuration. Please check IMU noise!"
<< std::endl;
return false;
}
for (int i = 0; i < 3; i++) {
paras.imunoise.gyr_arw[i] = arw * (D2R / 60.0);
paras.imunoise.acc_vrw[i] = vrw / 60.0;
paras.imunoise.gyrbias_std[i] = gbstd * (D2R / 3600.0);
paras.imunoise.accbias_std[i] = abstd * 1e-5;
paras.imunoise.gyrscale_std[i] = gsstd * 1e-6;
paras.imunoise.accscale_std[i] = asstd * 1e-6;
paras.initstate_std.imuerror.gyrbias[i] = gbstd * (D2R / 3600.0);
paras.initstate_std.imuerror.accbias[i] = abstd * 1e-5;
paras.initstate_std.imuerror.gyrscale[i] = gsstd * 1e-6;
paras.initstate_std.imuerror.accscale[i] = asstd * 1e-6;
}
paras.imunoise.corr_time *= 3600;
std::vector<double> mountAngle, leverArm, odo_measurement_std;
double odo_update_interval, wheelradius;
bool ifCompensateVelocity;
mountAngle = config["MisalignAngle"].as<std::vector<double>>();
leverArm = config["WheelLA"].as<std::vector<double>>();
odo_measurement_std = config["ODO_std"].as<std::vector<double>>();
paras.mountAngle = Eigen::Vector3d(mountAngle.data());
paras.leverArm = Eigen::Vector3d(leverArm.data());
paras.odo_measurement_std = Eigen::Vector3d(odo_measurement_std.data());
paras.odo_update_interval = config["ODO_dt"].as<double>();
paras.wheelradius = config["Wheel_Radius"].as<double>();
paras.ifCompensateVelocity = config["ifCompVel"].as<bool>();
paras.starttime = config["starttime"].as<double>();
return true;
}
从程序片段可以看出,将yaml中配置参数往Paras这个数据结构中装,就干了这一件事。
所以接下来就重点看下Paras数据结构构成。
typedef struct Paras {
// initial state and state standard deviation
NavState initstate;
NavState initstate_std;
// imu noise parameters
ImuNoise imunoise;
// install parameters
Eigen::Vector3d mountAngle = {0, 0, 0};
Eigen::Vector3d leverArm = {0, 0, 0};
Eigen::Vector3d odo_measurement_std = {0, 0, 0};
double odo_update_interval;
double wheelradius;
bool ifCompensateVelocity;
double starttime;
} Paras;
Paras数据结构中又包含,NavState、ImuNoise,继续展开看就行(为了不让篇幅过于长,让人阅读不适,点到为止,这是一贯宗旨)。
NavState包括三维位置、速度、欧拉角和imu误差数据结构ImuError,ImuError包括acc、gyro,bias和scale。
ImuNoise包括三维acc、gyro随机游走,bias和scale标准差。
mountAngle 对应论文中安装角误差;
leverArm 对应论文中杠臂误差。
只要在一张白纸上将数据结构构成、意义搞清楚,看后续程序会变得更加简单,也能更好的理解。
所以,看一些开源写的好代码,数据定义都非常清晰、相互包含关系逻辑性很强,看这种代码就像看艺术品一样。。。
二、读取数据
数据配置文件中包含数据长度、数据采样频率、开始时间和结束时间。根据数据路径和配置参数进行数据读取,如下:
ImuFileLoader imufile(imupath, imudatalen, imudatarate);
ImuFileLoader(const string &filename, int columns, int rate = 200) {
open(filename, columns, FileLoader::BINARY);
dt_ = 1.0 / (double)rate;
imu_.timestamp = 0;
}
文件使用标准文件方式读取open,关于数据的读取全部在对象imufile中进行了封装实现,如next,starttime,endtime。如下:
const IMU &next() {
imu_pre_ = imu_;
data_ = load();
imu_.timestamp = data_[0];
memcpy(imu_.angular_velocity.data(), &data_[1], 3 * sizeof(double));
memcpy(imu_.acceleration.data(), &data_[4], 3 * sizeof(double));
double dt = imu_.timestamp - imu_pre_.timestamp;
if (dt < 0.1) {
imu_.dt = dt;
} else {
imu_.dt = dt_;
}
return imu_;
}
double starttime() {
double starttime;
std::streampos sp = filefp_.tellg();
filefp_.seekg(0, std::ios_base::beg);
starttime = load().front();
filefp_.seekg(sp, std::ios_base::beg);
return starttime;
}
double endtime() {
double endtime = -1;
std::streampos sp = filefp_.tellg();
if (filetype_ == TEXT) {
filefp_.seekg(-2, std::ios_base::end);
char byte = 0;
auto pos = filefp_.tellg();
do {
pos -= 1;
filefp_.seekg(pos);
filefp_.read(&byte, 1);
} while (byte != '\n');
} else {
filefp_.seekg(-columns_ * sizeof(double), std::ios_base::end);
}
endtime = load().front();
filefp_.seekg(sp, std::ios_base::beg);
return endtime;
}
从上述程序片段可以看出:
每调用一次next()返回一帧imu数据(timestamp,dt(与前一帧数据时间差),gyro,acc);
每调用一次starttime返回当前帧时间戳;
调用一次endtime返回最后一帧时间戳。
seekg()与tellg()用法,详见seekg()与tellg()详解
三、newImuProcess
1.从yaml配置starttime读取第一帧imu数据;
将读取的数据添加到imuBuff_(类型std::deque)
wheelins.addImuData(imu_cur);
2.循环入口
while (true) {
imu_cur = imufile.next();
if (imu_cur.timestamp > endtime || imufile.isEof()) {
break;
}
wheelins.addImuData(imu_cur);
wheelins.newImuProcess();
timestamp = wheelins.timestamp();
navstate = wheelins.getNavState();
cov = wheelins.getCovariance();
writeNavResult(timestamp, navstate, navfile, imuerrfile);
writeSTD(timestamp, cov, stdfile);
percent = int((imu_cur.timestamp - starttime) / interval * 100);
if (percent - lastpercent >= 1) {
std::cout << "Processing: " << std::setw(3) << percent << "%\r"
<< std::flush;
lastpercent = percent;
}
}
(1)依次读取下一帧数据
wheelins.addImuData(imu_cur);
(2)处理wheelins.newImuProcess();
A.insPropagation(imupre_, imucur_)
a.补偿imu:imuCompensate
根据imu零偏和比例因子误差acc/gyro数据
b.insMesh
void INSMech::insMech(const PVA &pvapre, PVA &pvacur, const IMU &imupre,
const IMU &imucur) {
Eigen::Vector3d d_vfb, d_vfn, d_vgn, gl;
Eigen::Vector3d temp1, temp2, temp3;
Eigen::Vector3d imucur_dvel, imucur_dtheta, imupre_dvel, imupre_dtheta;
imucur_dvel = imucur.acceleration * imucur.dt;
imucur_dtheta = imucur.angular_velocity * imucur.dt;
imupre_dvel = imupre.acceleration * imupre.dt;
imupre_dtheta = imupre.angular_velocity * imupre.dt;
temp1 = imucur_dtheta.cross(imucur_dvel) / 2;
temp2 = imupre_dtheta.cross(imucur_dvel) / 12;
temp3 = imupre_dvel.cross(imucur_dtheta) / 12;
d_vfb = imucur_dvel + temp1 + temp2 + temp3;
d_vfn = pvapre.att.cbn * d_vfb;
gl << 0, 0, NormG;
d_vgn = gl * imucur.dt;
pvacur.vel = pvapre.vel + d_vfn + d_vgn;
Eigen::Vector3d midvel;
midvel = (pvacur.vel + pvapre.vel) / 2;
pvacur.pos = pvapre.pos + midvel * imucur.dt;
Eigen::Quaterniond qbb;
Eigen::Vector3d rot_bframe;
rot_bframe = imucur_dtheta + imupre_dtheta.cross(imucur_dtheta) / 12;
qbb = Rotation::rotvec2quaternion(rot_bframe);
pvacur.att.qbn = pvapre.att.qbn * qbb;
pvacur.att.cbn = Rotation::quaternion2matrix(pvacur.att.qbn);
pvacur.att.euler = Rotation::matrix2euler(pvacur.att.cbn);
}
从上述程序片段看出,基于中值积分,完成惯性导航位置、速度、姿态的求解,分别赋值为pvacurr.pos,pvacurr.vel,pvacurr.att(q,R,euler)。
c.根据论文中基于车轮中心速度约束算法推导的状态向量误差方程,完成卡尔曼状态预测
源码中状态向量没有考虑里程计比例因子误差和杠臂误差。

...
F.block(BG_ID, BG_ID, 3, 3) =
-1 / paras_.imunoise.corr_time * Eigen::Matrix3d::Identity();
F.block(BA_ID, BA_ID, 3, 3) =
-1 / paras_.imunoise.corr_time * Eigen::Matrix3d::Identity();
F.block(SG_ID, SG_ID, 3, 3) =
-1 / paras_.imunoise.corr_time * Eigen::Matrix3d::Identity();
F.block(SA_ID, SA_ID, 3, 3) =
-1 / paras_.imunoise.corr_time * Eigen::Matrix3d::Identity();
G.block(V_ID, VRW_ID, 3, 3) = pvapre_.att.cbn;
G.block(PHI_ID, ARW_ID, 3, 3) = pvapre_.att.cbn;
G.block(BG_ID, BGSTD_ID, 3, 3) = Eigen::Matrix3d::Identity();
G.block(BA_ID, BASTD_ID, 3, 3) = Eigen::Matrix3d::Identity();
G.block(SG_ID, SGSTD_ID, 3, 3) = Eigen::Matrix3d::Identity();
G.block(SA_ID, SASTD_ID, 3, 3) = Eigen::Matrix3d::Identity();
//对F(t)/G(t)离散化
Phi.setIdentity();
//F(k)= F(k)+ F(t)*dt
Phi = Phi + F * imucur.dt;
//G(k)= G(t)w*G(t)^t*dt
Qd = G * Qc_ * G.transpose() * imucur.dt;
Qd = (Phi * Qd * Phi.transpose() + Qd) / 2;
EKFPredict(Phi, Qd);
结合程序片段看出,Qc_为w(t),先求出F(t)/G(t),Phi,Qd是对F(t)/G(t)离散化。
void WheelINS::EKFPredict(Eigen::MatrixXd &Phi, Eigen::MatrixXd &Qd) {
assert(Phi.rows() == Cov_.rows());
assert(Qd.rows() == Cov_.rows());
Cov_ = Phi * Cov_ * Phi.transpose() + Qd;
delta_x_ = Phi * delta_x_;
}
更新状态delta_x_ 和协方差Cov_ 。
B.里程计更新ODOUpdate()
a.计算轮子速度wheelVelocity
void WheelINS::getWheelVelocity() {
double gyro_x_mean = 0.0;
int i = 0;
for (auto it = imuBuff_.begin(); it != imuBuff_.end(); ++it) {
gyro_x_mean += it->angular_velocity[0];
}
gyro_x_mean /= imuBuffsize;
wheelVelocity = -paras_.wheelradius * (gyro_x_mean);
}
imuBuff_尺度,长度为imuBuffsize = 0.1*IMU_RATE。
用imuBuff_角速度平均值和轮子半径计算轮子速度。
b.计算由杠臂投影计算得到轮速观测velocity_leverarm
Matrix3d C_nv = computeVehicleRotmat().transpose();
Matrix3d C_bv = C_nv * pvacur_.att.cbn;
Vector3d velocity_vframe = C_nv * pvacur_.vel;
Matrix3d angularVelocity_skew =
Rotation::skewSymmetric(imucur_.angular_velocity);
Matrix3d leverarm_skew = Rotation::skewSymmetric(paras_.leverArm);
Matrix3d velocitySkew_nframe = C_nv * Rotation::skewSymmetric(pvacur_.vel);
Vector3d velocity_leverarm = C_bv * angularVelocity_skew * paras_.leverArm;
Matrix3d WheelINS::computeVehicleRotmat() {
Vector3d vehicle_euler = Vector3d::Zero();
vehicle_euler[2] = pvacur_.att.euler[2] - M_PI / 2.0;
Matrix3d C_vn = Rotation::euler2matrix(vehicle_euler);
return C_vn;
}
如论文所述,认定imu与载体之间的偏航角偏差固定为90°。由杠臂投影计算得到杠臂投影到轮子中心的速度velocity_leverarm,由速度状态计算得到机体坐标系的速度velocity_vframe 。
则轮子速度观测:
Eigen::MatrixXd Zv = velocity_vframe + velocity_leverarm;
如论文公式:
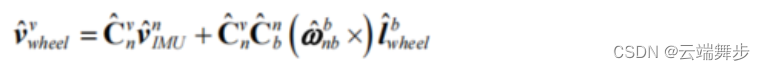
c.计算观测矩阵H
Hv.resize(3, RANK);
Hv.setZero();
Hv.block<3, 3>(0, V_ID) = C_nv;
Hv.block<3, 3>(0, PHI_ID) =
C_nv * Rotation::skewSymmetric(pvacur_.att.cbn * angularVelocity_skew *
paras_.leverArm);
Hv.block<3, 3>(0, BG_ID) = -C_bv * leverarm_skew;
Hv.block<3, 3>(0, SG_ID) =
-C_bv * leverarm_skew * imucur_.angular_velocity.asDiagonal();
Hv.block<3, 1>(0, 8) = -velocitySkew_nframe.block<3, 1>(0, 2);
d.计算观测噪声R
Eigen::MatrixXd Hv;
Eigen::MatrixXd Rv =
paras_.odo_measurement_std.cwiseProduct(paras_.odo_measurement_std)
.asDiagonal();
e.进行ekf更新
计算速度误差状态 = Zv - wheelVelocity(状态 - 观测)
EKFUpdate(Zv, Hv, Rv)
void WheelINS::EKFUpdate(Eigen::MatrixXd &dz, Eigen::MatrixXd &H,
Eigen::MatrixXd &R) {
assert(H.cols() == Cov_.rows());
assert(dz.rows() == H.rows());
assert(dz.rows() == R.rows());
assert(dz.cols() == 1);
auto temp = H * Cov_ * H.transpose() + R;
Eigen::MatrixXd K = Cov_ * H.transpose() * temp.inverse();
Eigen::MatrixXd I;
I.resizeLike(Cov_);
I.setIdentity();
I = I - K * H;
delta_x_ = delta_x_ + K * (dz - H * delta_x_);
Cov_ = I * Cov_ * I.transpose() + K * R * K.transpose();
}
公式如下:

对照上述代码片段,更新后验协方差和常规ekf有点区别。其它都是按照ekf五公式完全套下来即可。
f.更新后验状态向量
因为使用的误差卡尔曼,所以每次进行误差更新后,都要对状态进行更新。
stateFeedback();
void WheelINS::stateFeedback() {
pvacur_.pos -= delta_x_.block(P_ID, 0, 3, 1);
pvacur_.vel -= delta_x_.block(V_ID, 0, 3, 1);
Vector3d delta_att = delta_x_.block(PHI_ID, 0, 3, 1);
Eigen::Quaterniond qpn = Rotation::rotvec2quaternion(delta_att);
pvacur_.att.qbn = qpn * pvacur_.att.qbn;
pvacur_.att.cbn = Rotation::quaternion2matrix(pvacur_.att.qbn);
pvacur_.att.euler = Rotation::matrix2euler(pvacur_.att.cbn);
imuerror_.gyrbias += delta_x_.block(BG_ID, 0, 3, 1);
imuerror_.accbias += delta_x_.block(BA_ID, 0, 3, 1);
imuerror_.gyrscale += delta_x_.block(SG_ID, 0, 3, 1);
imuerror_.accscale += delta_x_.block(SA_ID, 0, 3, 1);
delta_x_.setZero();
}
如代码片段,更新完后验状态pvacur(pos、vel、att(q, R, euler), acc/gyro bias acc/gyro scale)。再对误差状态清零delta_x_.setZero()。
C.核验协方差checkCov()
void checkCov() {
for (int i = 0; i < RANK; i++) {
if (Cov_(i, i) < 0) {
std::cout << "Covariance is negative at " << std::setprecision(10)
<< timestamp_ << " !" << std::endl;
std::exit(EXIT_FAILURE);
}
}
}
从代码片段可以看出,这里核验协方差判断Cov_对角线元数若小于0,直接结束进程。
处理方式也比较粗暴,没有做异常后,系统重启处理,我想可能是因为系统只有轮子上安装了imu,系统中没有其它传感器可做异常接管的处理操作。
(3)更新状态存储
处理wheelins.newImuProcess()完,将最新状态和协方差写入到yaml指定的存储路径文本中。
timestamp = wheelins.timestamp();
navstate = wheelins.getNavState();
cov = wheelins.getCovariance();
writeNavResult(timestamp, navstate, navfile, imuerrfile);
writeSTD(timestamp, cov, stdfile);
最后同步实时输出当前处理进度:
percent = int((imu_cur.timestamp - starttime) / interval * 100);
if (percent - lastpercent >= 1) {
std::cout << "Processing: " << std::setw(3) << percent << "%\r"
<< std::flush;
lastpercent = percent;
}
四、后处理工作
就是对之前打开的文件进行关闭处理,非常简单。
imufile.close();
navfile.close();
imuerrfile.close();
stdfile.close();
五、总结
这样整个代码过程我们就全部看完了,综合下来,代码写的还是很不错的,简单、明了。代码部分与论文的主要区别:
1.状态向量为pvacur(pos、vel、att(q, R, euler), acc/gyro bias acc/gyro scale),没有考虑里程计比例因子误差和杠臂误差;
2.没有利用载体运动约束:零速更新和零速航向更新ZUPT/ZIHR。
参考文献
http://i2nav.cn/ueditor/jsp/upload/file/20210905/1630804325780076093.pdf
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- JWT的初级认识
- 大数据毕业设计:python房源数据爬虫分析预测系统+可视化 +商品房数据(源码+讲解视频)?
- Go语言网络编程介绍以及案例运用
- 利用 Amazon Bedrock 构建第一个生成式 AI 应用程序
- JavaScrip实现复选框的全选、全不选和反选
- 基于Java员工信息管理系统的设计与实现 毕业论文+任务书+开题报告+开题答辩PPT+毕业答辩PPT+答辩稿+演示知道视频+运行说明+项目源码及数据库文件
- 【Java SE语法篇】6.数组
- springboot+mysql大学生兼职网站-计算机毕业设计源码08011
- 【教程】代码混淆详解
- 【图像拼接】论文精读:Object-centered image stitching