【Leetcode 程序员面试金典 05.01】插入 —— 位运算

面试题 05.01 插入

给定两个整型数字N与M，以及表示比特位置的i与j（i <= j，且从 0 位开始计算）。

编写一种方法，使M对应的二进制数字插入N对应的二进制数字的第i ~ j位区域，不足之处用0补齐。具体插入过程如图所示。

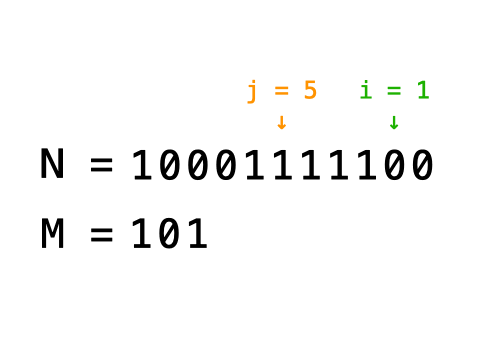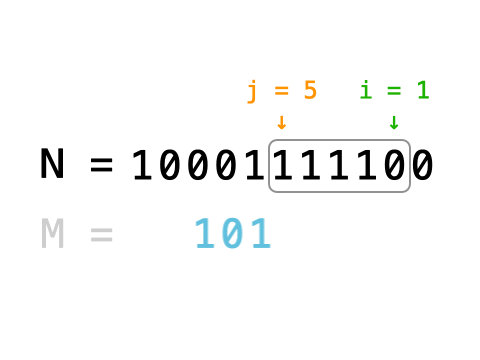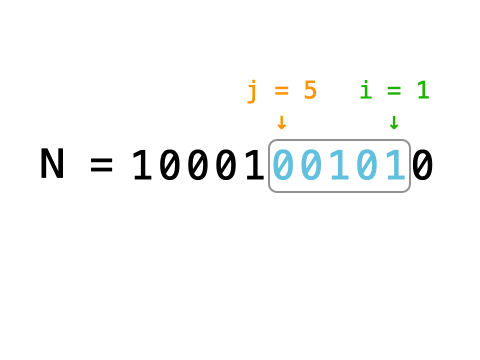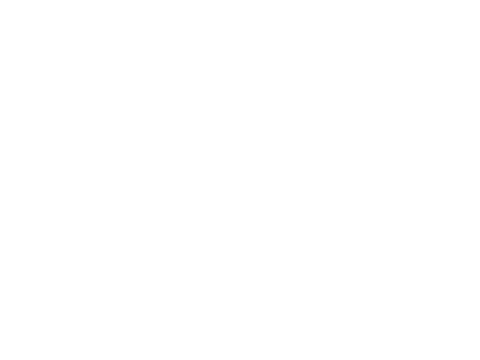
题目保证从i位到j位足以容纳M， 例如： M = 10011，则i～j区域至少可容纳5位。

示例1:

输入：N = 1024(10000000000), M = 19(10011), i = 2, j = 6
输出：N = 1100(10001001100)

示例2:

输入： N = 0, M = 31(11111), i = 0, j = 4
输出：N = 31(11111)

题目分析

简单的位运算问题，只需要把 N 的 i 到 j 位都置 0 后再和 M 左移 i 位的结果进行按位或即可

在 Java 语言中，int 类型的左移位数n≥32时，JVM 会将n对32取模，以确保左移的位数在 n 在 [0,31] 之间。因此，需使用0xffffffff << j << 1

public int insertBits(int N, int M, int i, int j) {
    int mask = (0xffffffff << j << 1) + ((1 << i) - 1);
    return N & mask | M << i;
}

位运算基础知识

1. 判断奇偶：

   • 奇：(x & 1) == 1?????(x & 1) != 0

   • 偶：(x & 1) == 0?????(x & 1) != 1

2. 乘（或除）以 2 的幂次：

   • x >> n????x / 2^n

   • x << n??? x * 2^n

3. 去除最后一位 1：x & (x - 1)

4. 得到最后一位 1：x & -x

5. 判断 2 的幂次：x & (x - 1) == 0

6. 交换两个数：a ^= b; b ^= a; a ^= b;

7. 交换符号：~x + 1?????-x

8. 取绝对值：(x ^ x >> size(x) - 1) - (x >> size(x) - 1)????x < 0 ? -x : x

9. 构造 n 个 1：(1 << n) - 1

10. 将最左边的 n 位清零：x & (~0 << n)

11. 获取 x 的第 n 位值（0 或 1）：(x >> n) & 1

12. 获取 x 的第 n 位的幂值：x & (1 << n)

13. 仅将第 n 位置为 1：x | (1 << n)

14. 仅将第 n 位置为 0：x & (~(1 << n))

15. 将 x 最高位至第 n 位（含）清零：x & ((1 << n) - 1)

16. 将第 n 位至第 0 位（含）清零：x & (~((1 << (n + 1)) - 1))

17. 取反第 n 位：x ^ (1 << n)

18. 异或满足交换律、结合律：a ^ b ^ a = b ^ (a ^ a) = b ^ 0 = b