统计学-R语言-6.3
前言
本篇文章是最后一个介绍参数估计的章节。
总体方差的区间估计
研究一个总体时,推断总体方差 使用的统计量为样本方差 。研究两个总体时,所关注的参数是两个总体的方差比(  ),用于推断的统计量则是两个样本的方差比(
),用于推断的统计量则是两个样本的方差比( 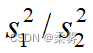 )。
)。
总体方差的区间估计(一个总体方差的估计)
估计一个总体的方差或标准差假定条件:
假设总体服从正态分布(原理与总体均值、总体比例区间估计不同)
样本方差的抽样分布服从自由度为n-1的 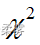 分布,用
分布,用 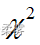 分布构造总体方差的置信区间
分布构造总体方差的置信区间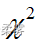 分布不是对称分布,无法由点估量±估计误差得到总体方差的置信区间
分布不是对称分布,无法由点估量±估计误差得到总体方差的置信区间


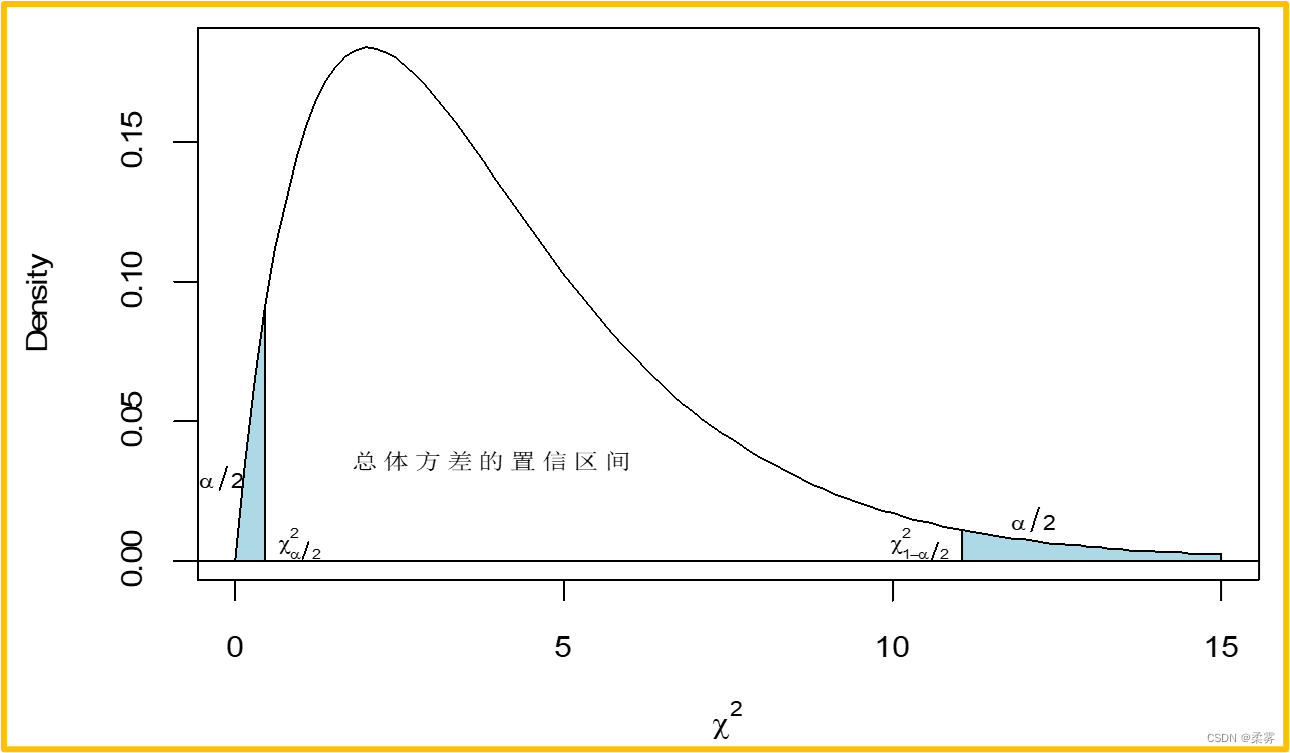
例题:
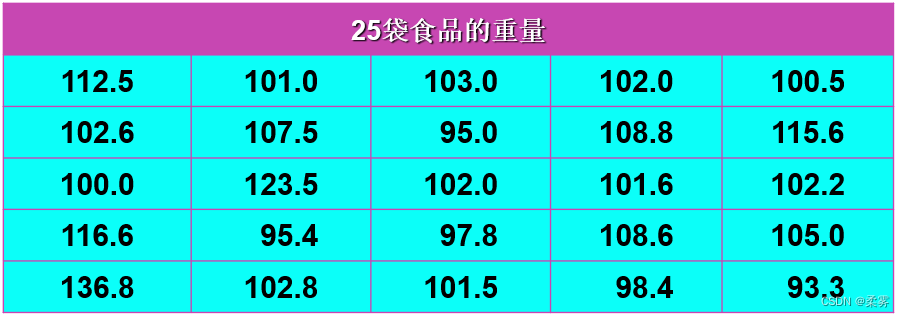
一家食品生产企业以生产袋装食品为主,现从某天生产的一批食品中随机抽取了25袋,测得每袋重量如下表所示。已知产品重量的分布服从正态分布。以95%的置信水平建立该种食品重量方差的置信区间
sigma.test(x, sigma=1, sigmasq=sigma"2, alternative=c(“two.sided”, “less”, “greater”), conf level=0. 95,)函数用于总体方差的检验。参数x为向量;sigma为假设的总体标准差,默认为1; sigmasq为假设的总体方差; alternative确定备择假设的形式,默认为"two. sided";conf.1eve指定置信水平,默认为0.95。
食品重量方差的置信区间(使用sigma.test函数)
load("C:/example/ch5/example5_2.RData")
library(TeachingDemos)
sigma.test(example5_2$食品重量,conf.level=0.95)$conf.int

总体方差的区间估计(两个总体方差比的估计)
在实际问题中经常会遇到比较两个总体方差的题,比如,希望比较用两种不同方法生产的产品性能的稳定性,比较不同测量工具的精确度,等等
由于两个样本的方差比服从F(n1-1,n2-1)分布,因此可用F分布构造两个总体方差比 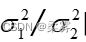 的置信区间,其原理可用下图来表示
的置信区间,其原理可用下图来表示
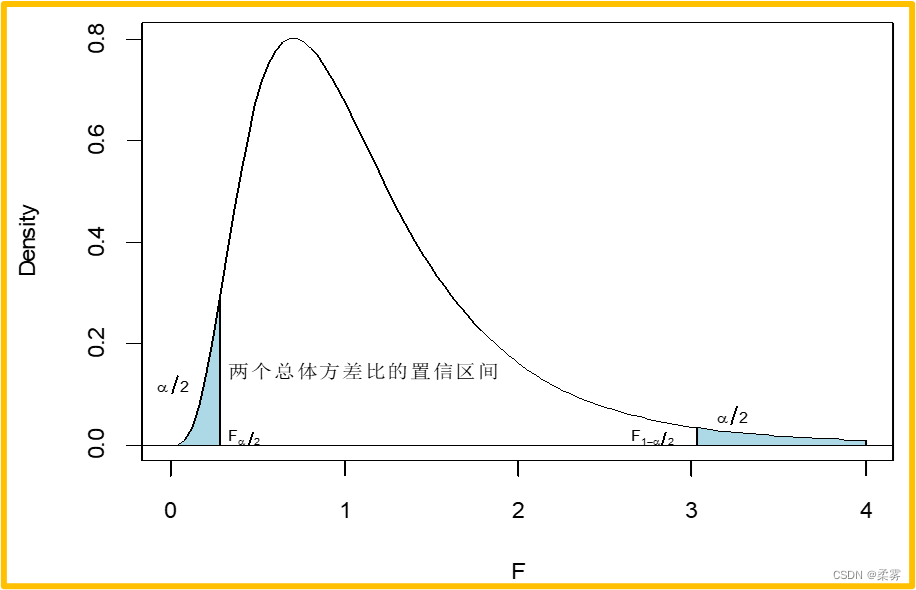

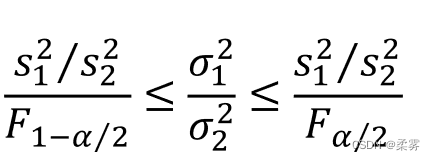
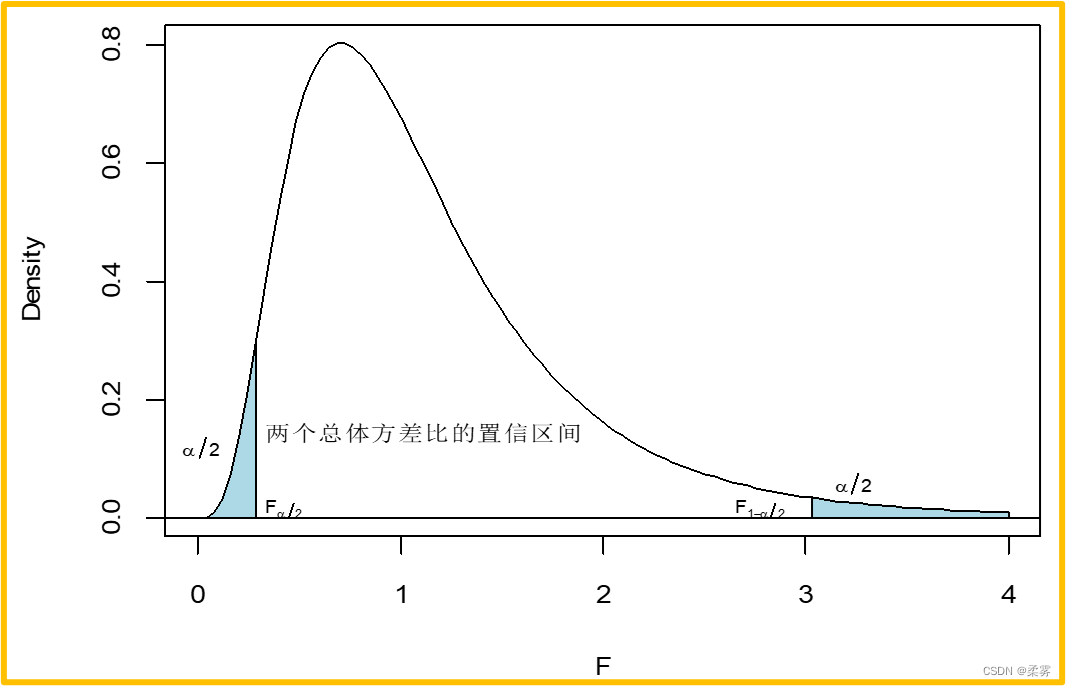
例题:
(数据: example5_4. RData)为估计两种方法组装产品所需时间的差异,分别对两种不同的组装方法各随机安排12个工人,每个工人组装一件产品所需的时间如下表所示。假定两种方法组装产品的时间服从正态分布,求以95%的置信水平建立两种方法组装产品所需时间方差比的置信区间。
函数var.test(x,y, ratio=1,alternative=“two.sided”)用于两个总体方差比的检验,参数x和y为向量 ;ratio为假设的两个总体方差比,默认为1。
两种方法组装产品所需时间方差比的置信区间
load("C:/example/ch5/example5_4.RData")
var.test(example5_4$方法一,example5_4$方法二,alternative="two.sided")$conf.int
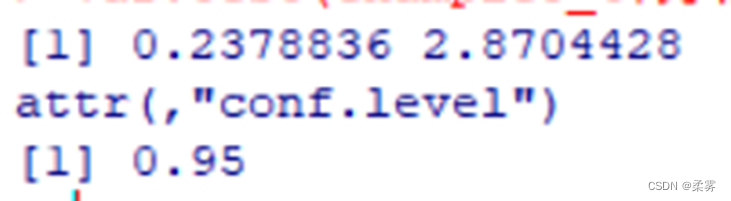
总结
以上三篇文章就是对参数估计的介绍。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!