记录每日LeetCode 162.寻找峰值与1901.寻找峰值II Java实现
发布时间:2023年12月19日
寻找峰值
题目描述:
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组?nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设?nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
初始代码:
class Solution {
public int findPeakElement(int[] nums) {
}
}示例1:
输入:nums = [1,2,3,1] 输出:2 解释:3 是峰值元素,你的函数应该返回其索引 2。
示例2:
输入:nums = [1,2,1,3,5,6,4] 输出:1 或 5 解释:你的函数可以返回索引 1,其峰值元素为 2; ? 或者返回索引 5, 其峰值元素为 6。
参考答案:
class Solution {
public int findPeakElement(int[] nums) {
// 返回任何一个峰值所在位置即可 说明寻找最大值即可
int max = 0;
for (int i = 0; i < nums.length; ++i) {
if (nums[i] > nums[max]) {
max = i;
}
}
return max;
}
}class Solution {
public int findPeakElement(int[] nums) {
if (nums.length == 1) {
return 0;
}
int left = 0, right = nums.length - 1, max = 0;
while (left <= right) {
// 首次需要判断左指针左侧是否有值
if (left - 1 >= 0) {
if (nums[left - 1] < nums[left] && nums[left] > nums[left + 1]) {
max = left;
break;
}
} else {
if (nums[left] > nums[left + 1]) {
max = left;
break;
}
}
// 首次需要判断右指针右侧是否有值
if (right + 1 == nums.length) {
if (nums[right] > nums[right - 1]) {
max = right;
break;
}
} else {
if (nums[right - 1] < nums[right] && nums[right] > nums[right + 1]) {
max = right;
break;
}
}
left++;
right--;
}
return max;
}
}class Solution {
public int findPeakElement(int[] nums) {
int left = 0, right = nums.length - 1, max = 0;
// 二分法
while (left < right) {
max = (left + right) >> 1;
//max = left + (right - left) / 2;
if (nums[max] > nums[max + 1]) {
right = max;
} else {
left = max + 1;
}
}
return left;
}
}寻找峰值II
题目描述:
一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。
给你一个 从 0 开始编号 的 m x n 矩阵 mat ,其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。
你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。
要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法
初始代码:
class Solution {
public int[] findPeakGrid(int[][] mat) {
}
}示例1:
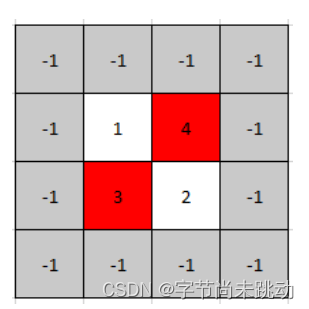
输入: mat = [[1,4],[3,2]] 输出: [0,1] 解释:?3 和 4 都是峰值,所以[1,0]和[0,1]都是可接受的答案。
示例2:
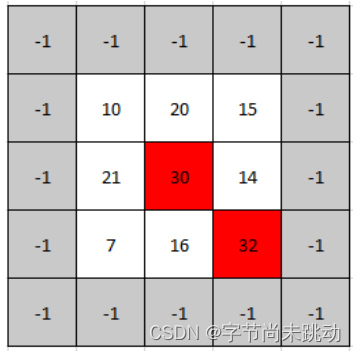
输入: mat = [[10,20,15],[21,30,14],[7,16,32]] 输出: [1,1] 解释:?30 和 32 都是峰值,所以[1,1]和[2,2]都是可接受的答案。
参考答案:
class Solution {
public int[] findPeakGrid(int[][] mat) {
int m = mat.length, n = mat[0].length;
int a = 0, b = 0;
// 暴力双for循环解决问题
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (mat[i][j] > mat[a][b]) {
a = i;
b = j;
}
}
}
return new int[]{a, b};
}
}class Solution {
public int[] findPeakGrid(int[][] mat) {
// 定义行数的左右指针
int left = 0, right = mat.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
// 传入行数得到最大值的列索引
int j = max(mat[mid]);
// 根据列中大小进行行切割
if (mat[mid][j] > mat[mid + 1][j]) {
right = mid;
} else {
left = mid + 1;
}
}
return new int[] {left, max(mat[left])};
}
private int max(int[] arr) {
int j = 0;
for (int i = 1; i < arr.length; ++i) {
if (arr[i] > arr[j]) {
j = i;
}
}
return j;
}
}
文章来源:https://blog.csdn.net/m0_65563175/article/details/135084021
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- YOLOv8改进 | 主干篇 | CSWinTransformer交叉形窗口网络
- Kubernetes-Scheduler调度器
- 2024年腾讯云4核8G12M轻量服务器测评
- 三元表达式竟然可以这样玩(多条件判断无限嵌套)
- 【BI&AI】Lecture 8 - EEG data analysis hands on
- cesium星空天空盒效果(附原图)
- VBA中类的解读及应用第八讲:实现定时器功能的自定义类事件
- 如何使用Ping命令检测网络连通性?
- 工智能基础知识总结--什么是KNN
- 从零开始学Hadoop,这些网站助你轻松掌握大数据技能!