redis数据结构（一）

redis是由C语言写的

一、简单动态字符串（simple dynamic string，SDS）

1.SDS的定义

每个sds.h/sdshdr结构表示一个SDS值：

举例：

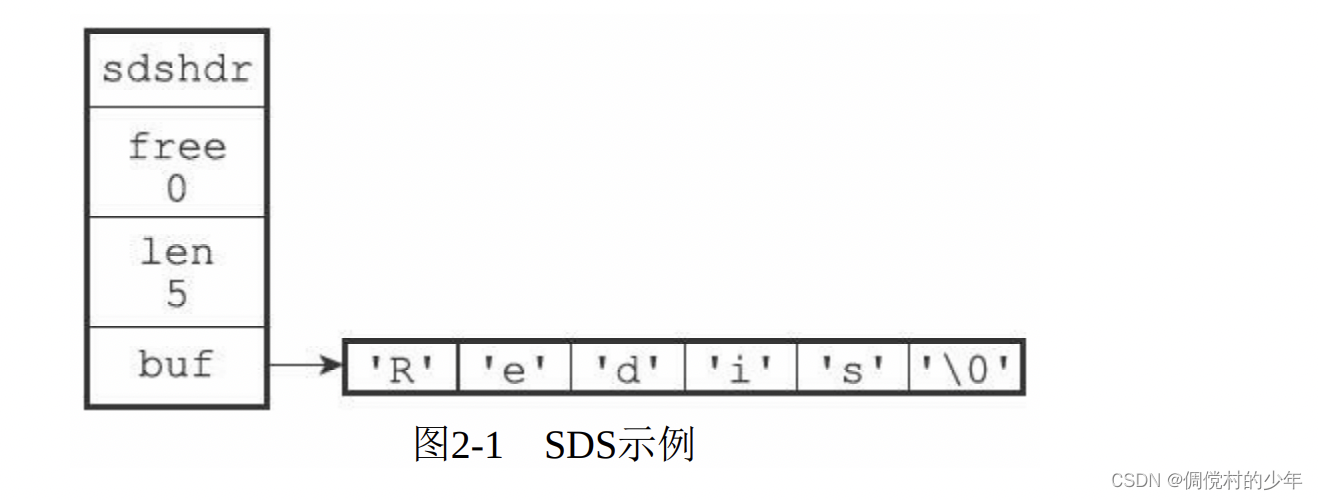
• free属性的值为0，表示这个SDS没有分配任何未使用空间。
• len属性的值为5，表示这个SDS保存了一个五字节长的字符串。
• buf属性是一个char类型的数组，数组的前五个字节分别保存 了’R’、‘e’、‘d’、‘i’、‘s’五个字符，而最后一个字节则保存了空字符’\0’。（保留了C字符串以空字符结尾的惯例）

2. SDS对C字符串的优化

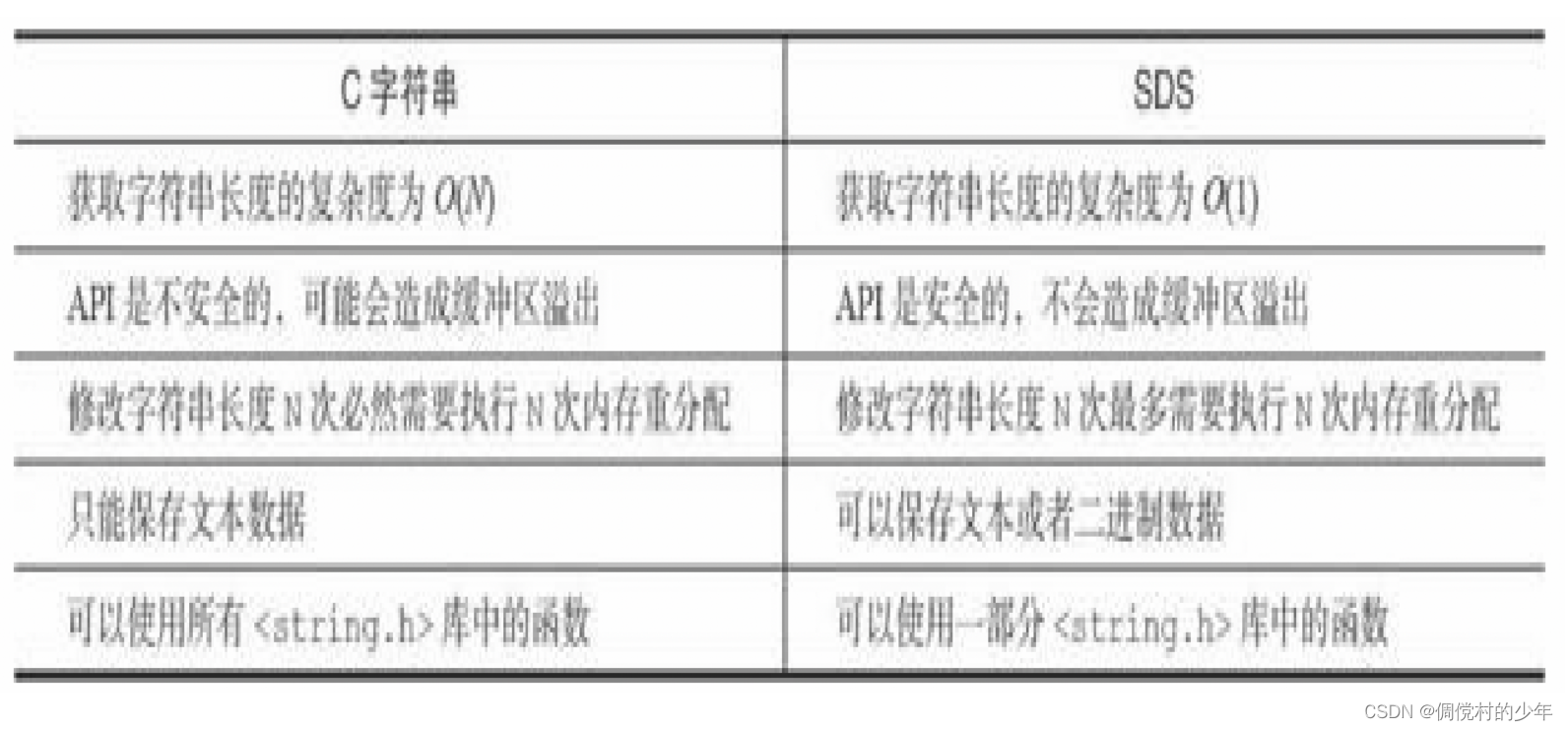
1. 获取长度复杂度：C字符串为O(n)， SDS为O(1)

2. 杜绝缓冲区溢出（可能会发生）：例如如果C字符串拼接，如果处于该字符串末尾地址空间没有充足的未被使用空间，那么可能覆盖之前存在此空间的数据；SDS会进行判断free是否足够，如果不够的话会自动扩展空间，具体如何扩展有相应的策略

3. 减少内存重分配次数

   1. 空间预分配
   2. 惰性空间释放

   下面详细解释

   C字符串发生长短变化时会发生内存重分配，需要执行系统调用，所以它通常是一个比较耗时的操作；同时redis作为数据库，数据时会被频繁修改的

4. 二进制安全

5. 兼容部分C字符串函数
   

空间预分配

如果对SDS进行修改之后，SDS的长度（也即是len属性的值）将 小于1MB，那么程序分配和len属性同样大小的未使用空间，这时SDS len属性的值将和free属性的值相同。举个例子，如果进行修改之后， SDS的len将变成13字节，那么程序也会分配13字节的未使用空间，SDS 的buf数组的实际长度将变成13+13+1=27字节（额外的一字节用于保存 空字符）。

如果对SDS进行修改之后，SDS的长度将大于等于1MB，那么程序 会分配1MB的未使用空间(free)。举个例子，如果进行修改之后，SDS的len将 变成30MB，那么程序会分配1MB的未使用空间，SDS的buf数组的实际 长度将为30MB+1MB+1byte。

通过空间预分配策略，Redis可以减少连续执行字符串增长操作所 需的内存重分配次数。

惰性空间释放

惰性空间释放用于优化SDS的字符串缩短操作：当SDS的API需要 缩短SDS保存的字符串时，程序并不立即使用内存重分配来回收缩短后 多出来的字节，而是使用free属性将这些字节的数量记录起来，并等待 将来使用。

二、链表

就是常见的链表数据结构，设计上基本没有什么特殊的。

三、字典

1. 字典实现

Redis的字典使用哈希表作为底层实现，一个哈希表里面可以有多 个哈希表节点，而每个哈希表节点就保存了字典中的一个键值对。

1.1 哈希表结构

1.2 哈希表节点结构

1.3字典结构

2. 哈希算法

【拉链法解决hash冲突】

当字典被用作数据库的底层实现，或者哈希键的底层实现时， Redis使用MurmurHash2算法来计算键的哈希值。

MurmurHash算法最初由Austin Appleby于2008年发明，这种算法的 优点在于，即使输入的键是有规律的，算法仍能给出一个很好的随机分 布性，并且算法的计算速度也非常快。

rehash

扩展和收缩哈希表的工作可以通过执行rehash（重新散列）操作来 完成，Redis对字典的哈希表执行rehash的步骤如下：

1）为字典的ht[1]哈希表分配空间，这个哈希表的空间大小取决于 要执行的操作，以及ht[0]当前包含的键值对数量（也即是ht[0].used属性 的值）：

• 如果执行的是扩展操作，那么ht[1]的大小为第一个大于等于 ht[0].used*2的2 n（2的n次方幂）；
• 如果执行的是收缩操作，那么ht[1]的大小为第一个大于等于 ht[0].used的2 n。

2）将保存在ht[0]中的所有键值对rehash到ht[1]上面：rehash指的是 重新计算键的哈希值和索引值，然后将键值对放置到ht[1]哈希表的指定 位置上。

3）当ht[0]包含的所有键值对都迁移到了ht[1]之后（ht[0]变为空 表），释放ht[0]，将ht[1]设置为ht[0]，并在ht[1]新创建一个空白哈希 表，为下一次rehash做准备。

4. 渐进式rehash

以下是哈希表渐进式rehash的详细步骤：

1）为ht[1]分配空间，让字典同时持有ht[0]和ht[1]两个哈希表。

2）在字典中维持一个索引计数器变量rehashidx，并将它的值设置 为0，表示rehash工作正式开始。

3）在rehash进行期间，每次对字典执行添加、删除、查找或者更新 操作时，程序除了执行指定的操作以外，还会顺带将ht[0]哈希表在 rehashidx索引上的所有键值对rehash到ht[1]，当rehash工作完成之后，程 序将rehashidx属性的值增一。

4）随着字典操作的不断执行，最终在某个时间点上，ht[0]的所有 键值对都会被rehash至ht[1]，这时程序将rehashidx属性的值设为-1，表 示rehash操作已完成。

渐进式rehash的好处在于它采取分而治之的方式，将rehash键值对 所需的计算工作均摊到对字典的每个添加、删除、查找和更新操作上， 从而避免了集中式rehash而带来的庞大计算量。

渐进式rehash执行期间的哈希表操作

因为在进行渐进式rehash的过程中，字典会同时使用ht[0]和ht[1]两 个哈希表，所以在渐进式rehash进行期间，字典的删除（delete）、查找 （find）、更新（update）等操作会在两个哈希表上进行。例如，要在 字典里面查找一个键的话，程序会先在ht[0]里面进行查找，如果没找到 的话，就会继续到ht[1]里面进行查找，诸如此类（会查找两次，但是对于hash来说时间损失很少）。

另外，在渐进式rehash执行期间，新添加到字典的键值对一律会被 保存到ht[1]里面，而ht[0]则不再进行任何添加操作，这一措施保证了 ht[0]包含的键值对数量会只减不增，并随着rehash操作的执行而最终变 成空表。

小结

还是分而治之、空间换取空间的思想，创建两个hash表，当开始操作元素的时候才开始迁移那个元素，这个与以往hash实现有点区别值得学习。

主要还是因为redis是单线程的原因，如果集中在某一次put的时候进行rehash，那么这一次操作就会较慢。可以类比ConcurrentHashMap（注意这里不能类比HashMap，因为hashmap并不是多线程安全的，但是redis有多个连接去操作仍然是线程安全的，原因如上，但是由于是内存操作所以很快，多线程无感），ConcurrentHashMap会进行多线程协助扩容，所以就大大缩短了时间，最终即使停顿了扩容的时间，但是也不会太慢。

四、跳跃表

跳跃表（skiplist）是一种有序数据结构，它通过在每个节点中维持 多个指向其他节点的指针，从而达到快速访问节点的目的。

跳跃表支持平均O（logN）、最坏O（N）复杂度的节点查找，还可 以通过顺序性操作来批量处理节点。 在大部分情况下，跳跃表的效率可以和平衡树相媲美，并且因为跳跃表的实现比平衡树要来得更为简单，所以有不少程序都使用跳跃表来 代替平衡树。

Redis使用跳跃表作为有序集合键的底层实现之一，如果一个有序集合包含的元素数量比较多，又或者有序集合中元素的成员 （member）是比较长的字符串时，Redis就会使用跳跃表来作为有序集合键的底层实现。

重要的点：层

跳跃表节点的level数组可以包含多个元素，每个元素都包含一个指 向其他节点的指针，程序可以通过这些层来加快访问其他节点的速度， 一般来说，层的数量越多，访问其他节点的速度就越快。

每次创建一个新跳跃表节点的时候，程序都根据幂次定律（power law，越大的数出现的概率越小）随机生成一个介于1和32之间的值作为 level数组的大小，这个大小就是层的“高度”。

此数据结构后面仔细分析。

五、整数集合

整数集合（intset）是集合键的底层实现之一，当一个集合只包含整 数值元素，并且这个集合的元素数量不多时，Redis就会使用整数集合 作为集合键的底层实现。

1.整数集合的实现

整数集合（intset）是Redis用于保存整数值的集合抽象数据结构， 它可以保存类型为int16_t、int32_t或者int64_t的整数值，并且保证集合 中不会出现重复元素。

虽然intset结构将contents属性声明为int8_t类型的数组，但实际上 contents数组并不保存任何int8_t类型的值，contents数组的真正类型取决 于encoding属性的值：

类型	数值范围
int16_t	-32768–32767
int32_t	-2147483648–2147483647
int64_t	-9223372036854775808–9223372036854775807

2.升级

每当我们要将一个新元素添加到整数集合里面，并且新元素的类型 比整数集合现有所有元素的类型都要长时，整数集合需要先进行升级 （upgrade），然后才能将新元素添加到整数集合里面。 升级整数集合并添加新元素共分为三步进行：
1）根据新元素的类型，扩展整数集合底层数组的空间大小，并为 新元素分配空间。

2）将底层数组现有的所有元素都转换成与新元素相同的类型，并将类型转换后的元素放置到正确的位上，而且在放置元素的过程中，需 要继续维持底层数组的有序性质不变。

3）将新元素添加到底层数组里面。

迁移的过程比较有意思：



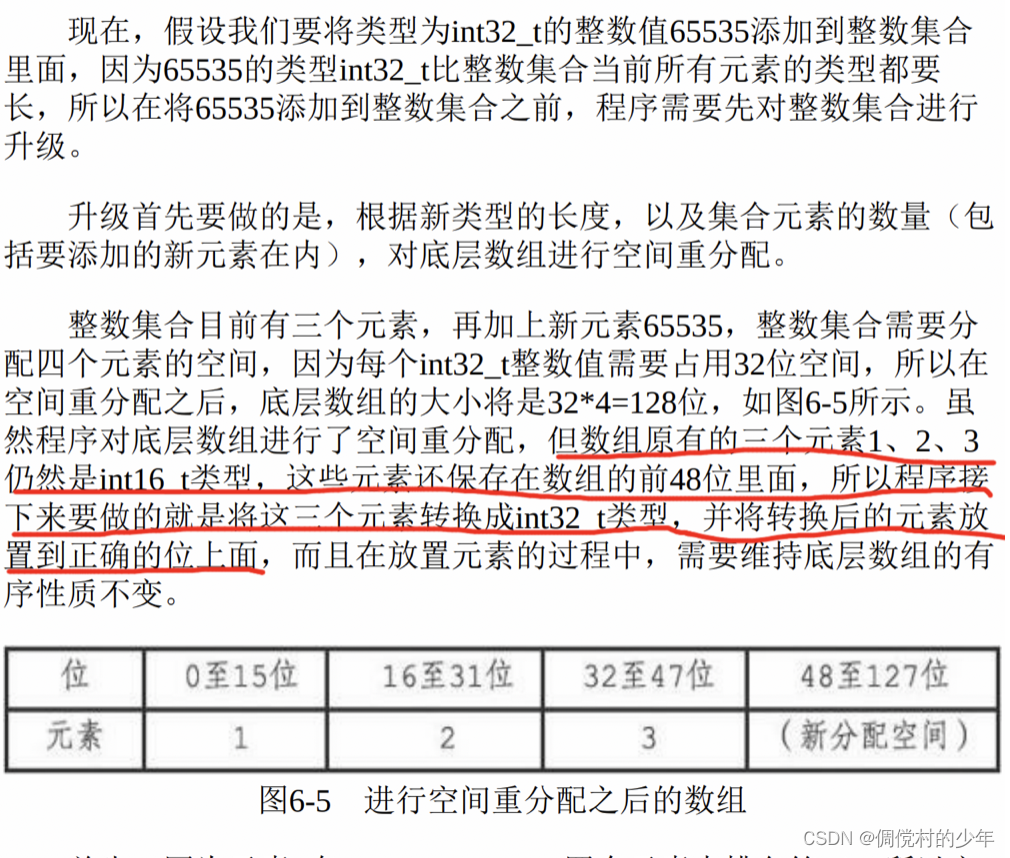
【只会升级不会降级】

3.升级的好处与坏处

好处：

1. 提升灵活性
2. 节约内存

坏处：（个人认为）

增加元素不论是否会导致升级，只要增加元素就必然会导致内存重分配，需要时间消耗

六、压缩列表

压缩列表（ziplist）是列表键和哈希键的底层实现之一。当一个列 表键只包含少量列表项，并且每个列表项要么就是小整数值，要么就是 长度比较短的字符串，那么Redis就会使用压缩列表来做列表键的底层实现。

1.压缩列表的构成

压缩列表是Redis为了节约内存而开发的，是由一系列特殊编码的 连续内存块组成的顺序型（sequential）数据结构。一个压缩列表可以包 含任意多个节点（entry），每个节点可以保存一个字节数组（也就是字符串）或者一个整数值。

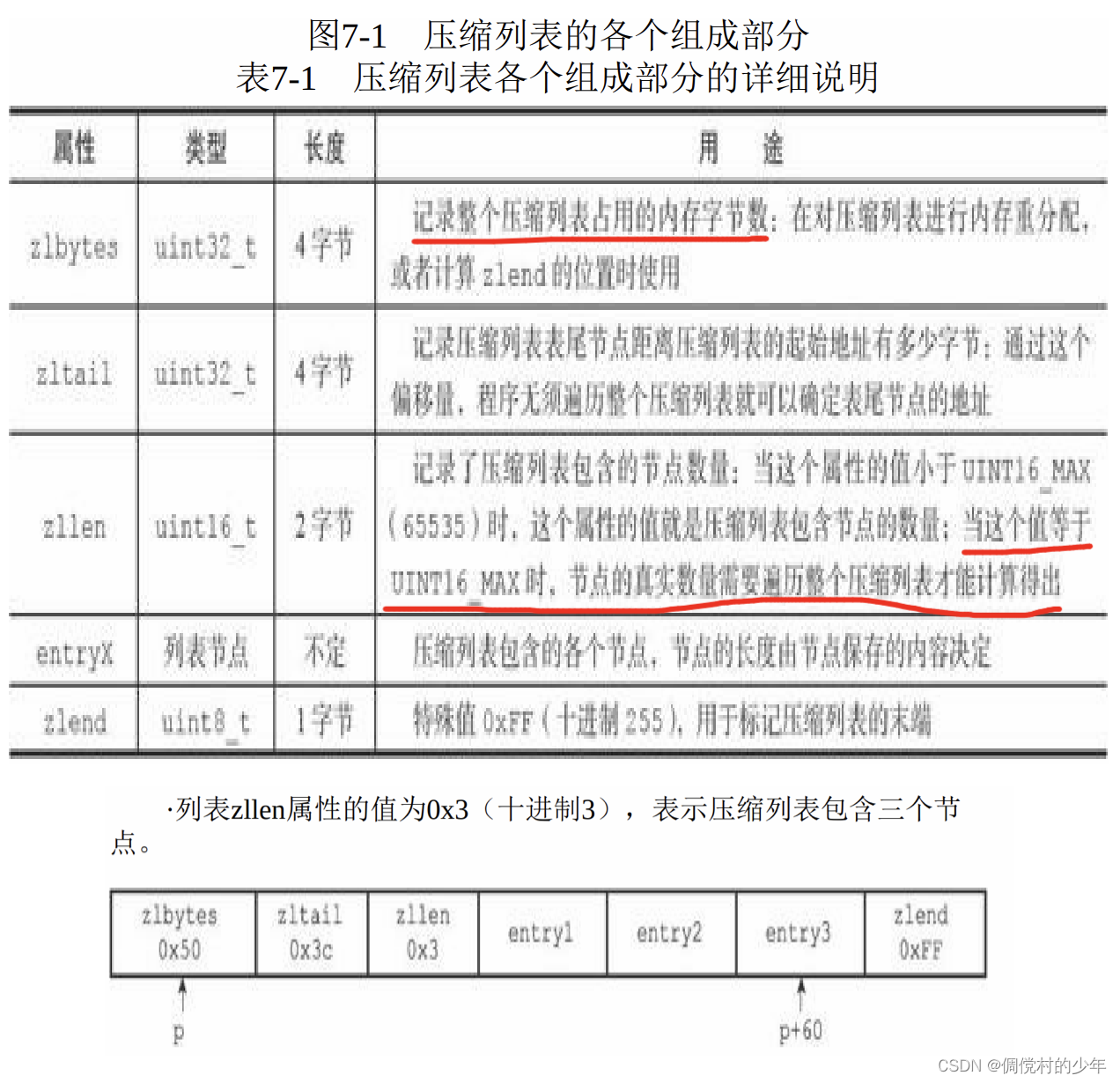
只标记了末端指针，所以说通常是从尾部遍历。

2. 节点构成

每个压缩列表节点可以保存一个字节数组或者一个整数值，其中，
字节数组可以是以下三种长度的其中一种：

• 长度小于等于63（261）字节的字节数组；
• 长度小于等于16383 （2^14-1） 字节的字节数组；
• 长度小于等于4294967295（2^32-1） 字节的字节数组；

而整数值则可以是以下六种长度的其中一种：

• 4位长，介于0至12之间的无符号整数；
• 1字节长的有符号整数；
• 3字节长的有符号整数；
• int16t类型整数：
• int32_t类型整数；
• int64t类型整数。
  每个压缩列表节点都由previous_entry_length、encoding、content三 个部分组成，如图7-4所示。
  

2.1 previous_entry_length

节点的previous_entry_length属性以字节为单位，记录了压缩列表中 前一个节点的长度。previous_entry_length属性的长度可以是1字节或者5 字节：

• 如果前一节点的长度小于254字节，那么previous_entry_length属性 的长度为1字节：前一节点的长度就保存在这一个字节里面。
• 如果前一节点的长度大于等于254字节，那么previous_entry_length 属性的长度为5字节：其中属性的第一字节会被设置为0xFE（十进制值 254），而之后的四个字节则用于保存前一节点的长度。

注意：下面的0x代表用的是16进制的

2.2 encoding

节点的encoding属性记录了节点的content属性所保存数据的类型以 及长度：

• 一字节、两字节或者五字节长，值的最高位为00、01或者10的是 字节数组编码：这种编码表示节点的content属性保存着字节数组，数组 的长度由编码除去最高两位之后的其他位记录；
• 一字节长，值的最高位以11开头的是整数编码：这种编码表示节 点的content属性保存着整数值，整数值的类型和长度由编码除去最高两 位之后的其他位记录； 表7-2记录了所有可用的字节数组编码，而表7-3则记录了所有可用 的整数编码。表格中的下划线“_”表示留空，而b、x等变量则代表实际 的二进制数据，为了方便阅读，多个字节之间用空格隔开。
  

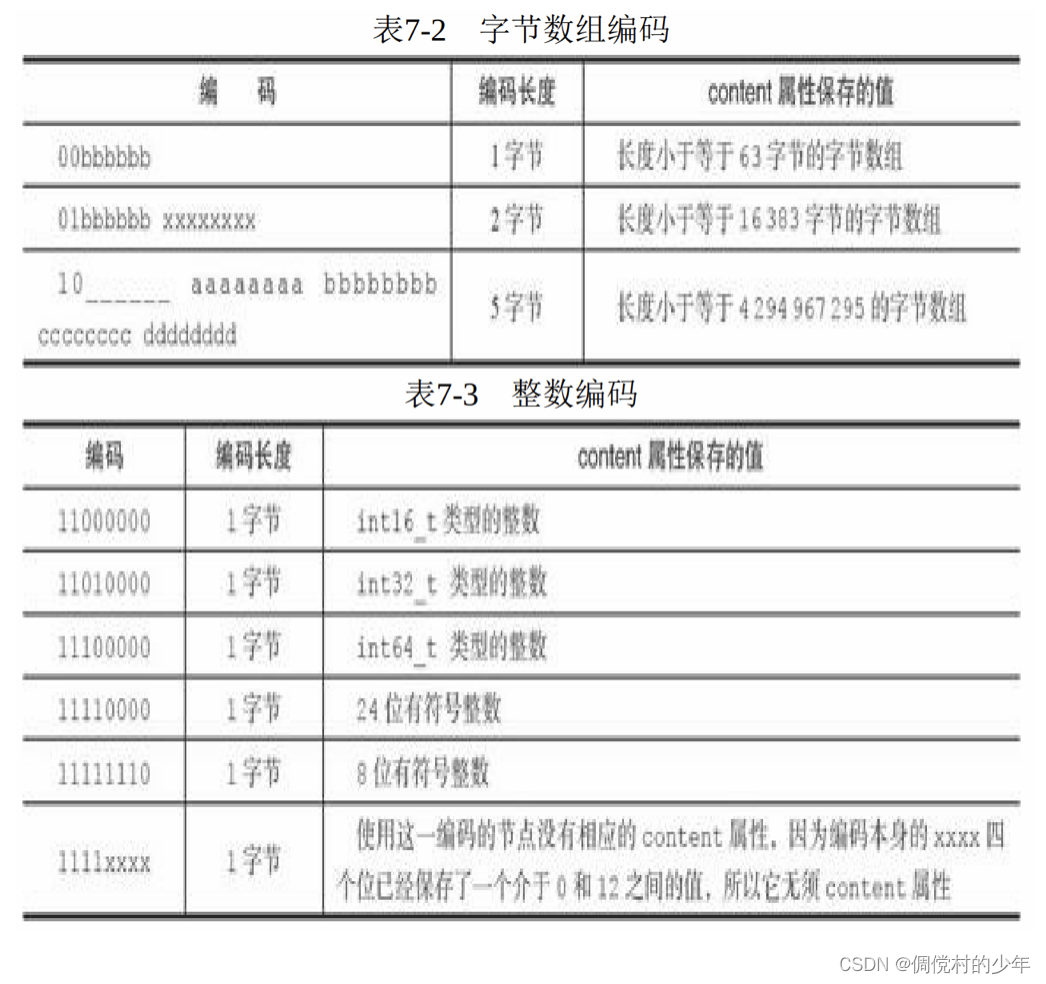
2.3 content

节点的content属性负责保存节点的值，节点值可以是一个字节数组 或者整数，值的类型和长度由节点的encoding属性决定。

3. 连锁更新

如果在某个节点前面增加一个元素，此元素长度大于254，导致当前节点的previous_entry_length原先是一个字节就要增加到5个字节，如果当前节点正好是254，那么此时当前节点就会大于254，就会引发下一个节点更新，以此类推。

因为连锁更新在最坏情况下需要对压缩列表执行N次空间重分配操 作，而每次空间重分配的最坏复杂度为O（N），所以连锁更新的最坏 复杂度为O（n*n）。

要注意的是，尽管连锁更新的复杂度较高，但它真正造成性能问题
的几率是很低的：
? 首先，压缩列表里要恰好有多个连续的、长度介于250字节至253字节之间的节点，连锁更新才有可能被引发，在实际中，这种情况并不多见；
?其次，即使出现连锁更新，但只要被更新的节点数量不多，就会对性能造成任何影响：比如说，对三五个节点进行连锁更新是绝对不会影响性能的；
因为以上原因，ziplistPush等命令的平均复杂度仅为O(N)，在实际中，我们可以放心地使用这些函数，而不必担心连锁更新会影响压缩列走的性能。

下一篇文章再向大家介绍最后一种数据结构：对象。