深度学习 | 常见问题及对策(过拟合、欠拟合、正则化)
?
?
?1、训练常见问题
?
1.1、模型架构设计
?????????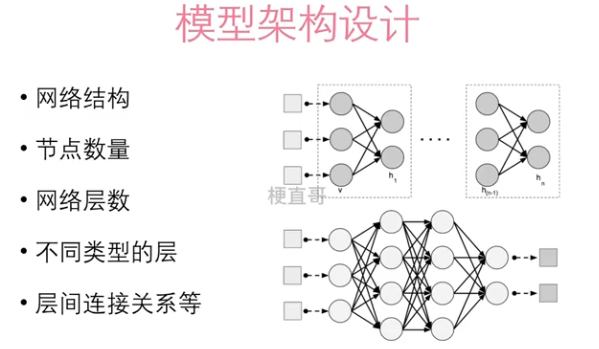
??????? 关于隐藏层的一个万能近似定理:
????????Universal Approximation Theorem:一个具有足够多的隐藏节点的多层前馈神经网络,可以逼近任意连续的函数。(Cybenko, 1989)—— 必须包含至少一种有挤压性质的激活函数。
????????
?
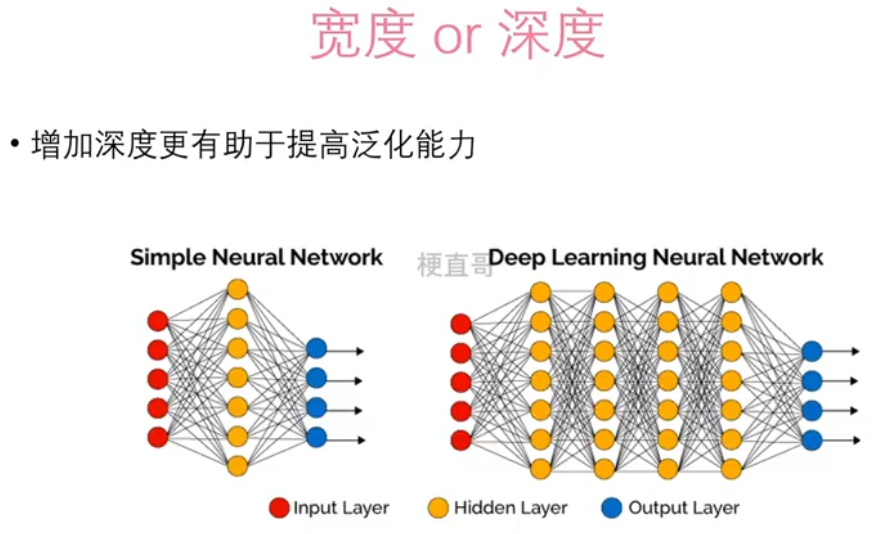
1.2、宽度 / 深度
????????
1.3、过拟合
?????????Overfitting:模型在训练数据上表现良好,在测试数据上不佳
????????泛化能力:训练后的模型应用到新的、未知的数据上的能力
????????产生原因:通常是由模型复杂度过高导致的
????????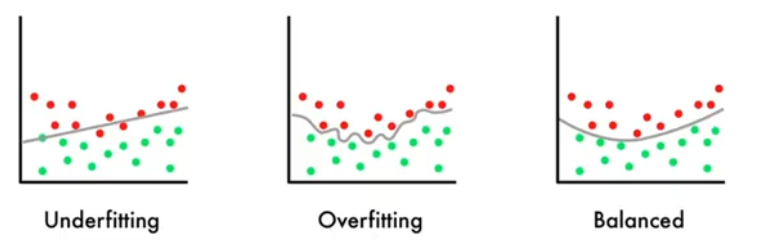
1.4、欠拟合
????????Underfitting:学习能力不足,无法学习到数据集中的“一般规律
????????产生原因:模型学习能力较弱,而数据复杂度较高的情况
相互关系:
????????
?
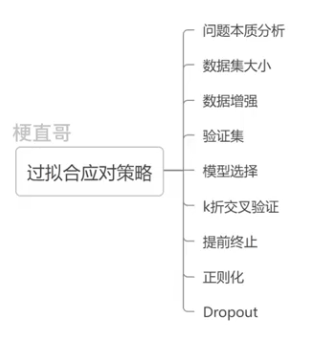
?1.5、过拟合应对策略
?
???????? 本质都是数据和模型匹配问题。可以从以下三种方法入手:
????????????????数据复杂度
????????????????模型复杂度
????????????????训练策略
?
????????
?????????
?????????
????????
????????
????????
????????
?
2、正则化
?
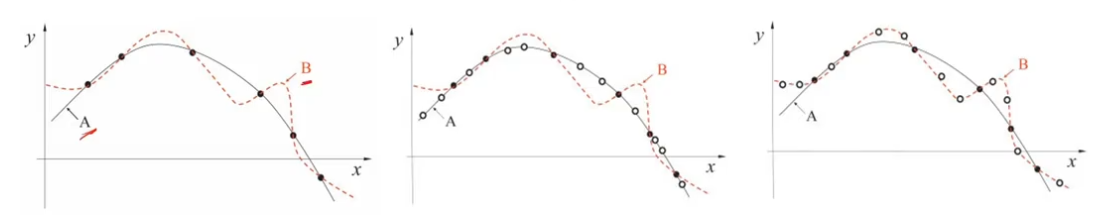
??????? 正则化:对学习算法的修改,目的是减少泛化误差,而不是训练误差。
????????
没有免费午餐定理:脱离具体问题,空谈什么模型更好没有意义。
????????没有一种算法或者模型能够在所有的场景中都表现良好。
????????正则化是一种权衡过拟合和欠拟合的手段。
????????
?
2. 1、L2正则化
?
?????????通过给模型的损失函数添加一个模型参数的平方和的惩罚项来实现正则化。
????????
???????? L 为范数。
?? ????? 在机器学习中也被称为 岭回归。
?
2.2、L1正则化
????????通过在损失函数中加入对模型参数权值矩阵中各元素绝对值之和的惩罚项,来限制模型参数的值。
????????
??? ?? 在机器学习中也被称为 LASSO回归。
?
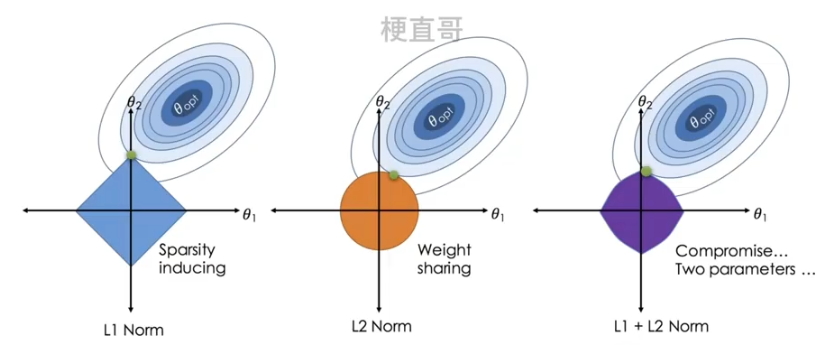
L1正则化和L2正则化空间解释:
????????机器学习 | 过拟合与正则化、模型泛化与评价指标-CSDN博客
L1正则化和L2正则化异同对比:
?????????L1正则化更倾向于产生稀疏解,适于特征选择。
????????L2正则化更倾向于小的非零权值,更适用于优化问题,使得权值更加平滑。
?????????
?
?
2.3、范数惩罚
?
????????将L1和L2正则化扩展到一般情况, λ 表示系数,越大表示惩罚程度越大。
?????????
??????? 神经网络中一般参数会包含两种,y = f ( w X + b )
??????? w 是仿射变换和偏置 b ,通常情况下我们只考虑对参数 w 作惩罚,这是由于在拟合偏置 b 时所需数据量比较少就可以拟合的很好了。
?
2.4、权重衰减 Weight Decay
?????????
???????? 直接修改最优化过程中参数迭代的方程:
????????
???????? 当使用随机梯度下降 SGD 时,就等价于 L2正则化。
????????
2.5、Dropout方法
?
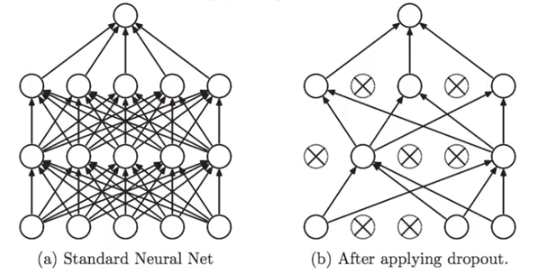
工作原理:
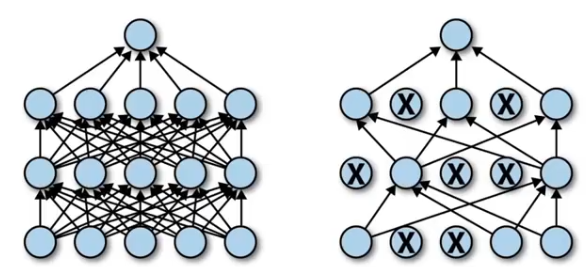
?????????在训练过程中随机删除(即将其权重设为零)一些神经元,从而使模型不能够依赖于某些特定的特征。
????????只用在训练期间,不用在测试期间。
?????????
主要步骤:????????
????????指定一个保留比例p;
????????每层每个神经元,以p 的概率保留,以1-p 的概率将权重设为零;
????????训练中使用保留的神经元进行前向、反向传播;
????????测试过程,将所有权重乘以p。
?
?直观理解:
??????? 相当于把一个网络拆分;
??????? 由多个子网络构成集成学习,bagging。
????????
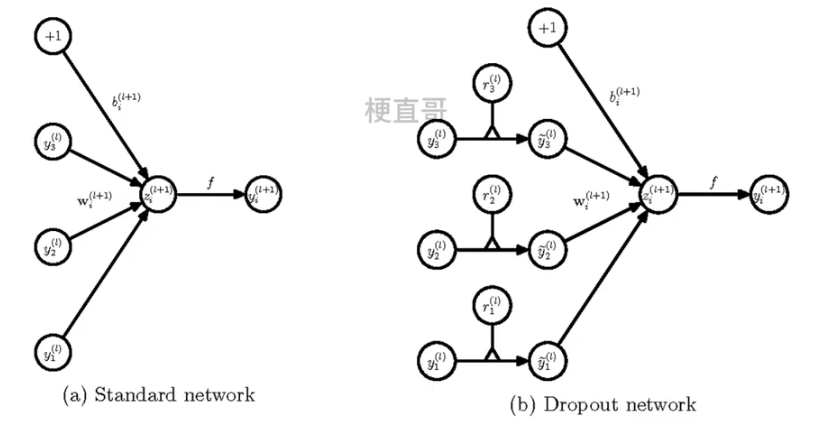
?神经网络中的使用:
????????在训练网络的每个单元都要添加概率计算。
??????? 添加 r ~
????????
?
?为什么能减少过拟合:
????????本质是Bagging集成学习,平均化作用;
????????减少神经元之间复杂的关系,迫使模型寻找显著的特征;
????????类似性别在生物进化中的角色。
????????
优缺点:
????????可以有效地减少过拟合,简单方便,实用有效。
??????? 降低训练效率(多了分拆、计算概率),损失函数不够明确。
?????????
?
代码实现:
# 导入必要的库
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
# 随机数种子
torch.manual_seed(2333)
# 定义超参数
num_samples = 20 # 样本数
hidden_size = 200 # 隐藏层大小
num_epochs = 500 # 训练轮数数据生成
# 生成训练集
x_train = torch.unsqueeze(torch.linspace(-1, 1, num_samples), 1)
y_train = x_train + 0.3 * torch.randn(num_samples, 1)
# 测试集
x_test = torch.unsqueeze(torch.linspace(-1, 1, num_samples), 1)
y_test = x_test + 0.3 * torch.randn(num_samples, 1)
# 绘制训练集和测试集
plt.scatter(x_train, y_train, c='r', alpha=0.5, label='train')
plt.scatter(x_test, y_test, c='b', alpha=0.5, label='test')
plt.legend(loc='upper left')
plt.ylim((-2, 2))
plt.show()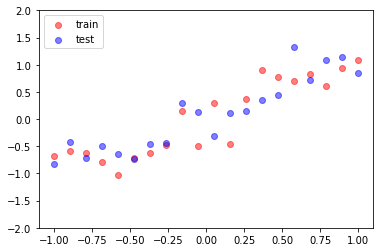
模型定义
# 定义一个可能会过拟合的网络
net_overfitting = torch.nn.Sequential(
torch.nn.Linear(1, hidden_size),
torch.nn.ReLU(),
torch.nn.Linear(hidden_size, hidden_size),
torch.nn.ReLU(),
torch.nn.Linear(hidden_size, 1),
)
# 定义一个包含 Dropout 的网络
net_dropout = torch.nn.Sequential(
torch.nn.Linear(1, hidden_size),
torch.nn.Dropout(0.5), # p=0.5
torch.nn.ReLU(),
torch.nn.Linear(hidden_size, hidden_size),
torch.nn.Dropout(0.5), # p=0.5
torch.nn.ReLU(),
torch.nn.Linear(hidden_size, 1),
)模型训练
# 定义优化器和损失函数
optimizer_overfitting = torch.optim.Adam(net_overfitting.parameters(), lr=0.01)
optimizer_dropout = torch.optim.Adam(net_dropout.parameters(), lr=0.01)
# 损失函数
criterion = nn.MSELoss()
# 分别进行训练
for i in range(num_epochs):
# overfitting的网络:预测、损失函数、反向传播
pred_overfitting = net_overfitting(x_train)
loss_overfitting = criterion(pred_overfitting, y_train)
optimizer_overfitting.zero_grad()
loss_overfitting.backward()
optimizer_overfitting.step()
# 包含dropout的网络:预测、损失函数、反向传播
pred_dropout = net_dropout(x_train)
loss_dropout = criterion(pred_dropout, y_train)
optimizer_dropout.zero_grad()
loss_dropout.backward()
optimizer_dropout.step()预测和可视化
# 在测试过程中不使用 Dropout
net_overfitting.eval()
net_dropout.eval()
# 预测
test_pred_overfitting = net_overfitting(x_test)
test_pred_dropout = net_dropout(x_test)
# 绘制拟合效果
plt.scatter(x_train, y_train, c='r', alpha=0.3, label='train')
plt.scatter(x_test, y_test, c='b', alpha=0.3, label='test')
plt.plot(x_test, test_pred_overfitting.data.numpy(), 'r-', lw=2, label='overfitting')
plt.plot(x_test, test_pred_dropout.data.numpy(), 'b--', lw=2, label='dropout')
plt.legend(loc='upper left')
plt.ylim((-2, 2))
plt.show()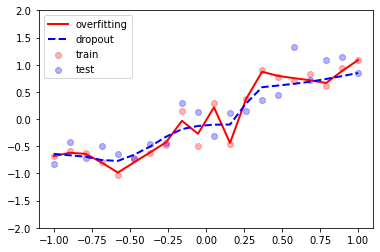
?
?3、梯度消失与梯度爆炸
3.1、梯度的重要性
?
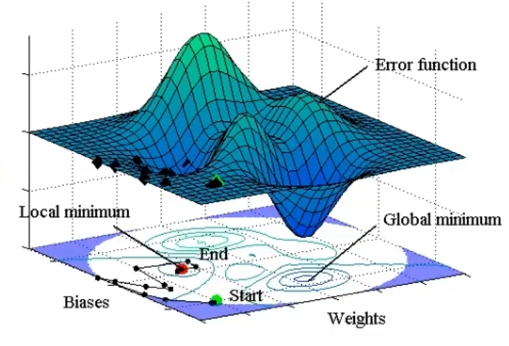
??????? 深度神经网络就是非线性多元函数。
????????优化模型就是找到合适权重,最小化损失函数。
????????
????????
?
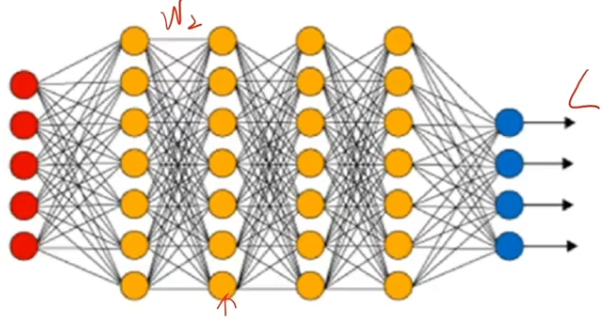
3.2、反向传播的内在问题
????????链式求导法则本身就是激活函数的偏导数连乘。
????????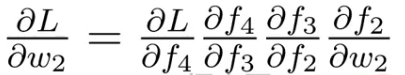
????????
3.3、梯度消失
??????? sigmiod函数:
??????????????? 梯度不超过 0.5。
????????激活函数的导数小于1容易发生梯度消失。
??????? 
3.4、梯度爆炸
????????梯度可在更新中累积,变成非常大,导致网络不稳定或者模型溢出。
????????原因之一:深层网络;
????????原因之二:初始化权重的值过大。
3.5、解决办法
????????预训练加微调
????????梯度剪切、正则
????????ReLU激活函数
????????Batchnorm
????????残差结构
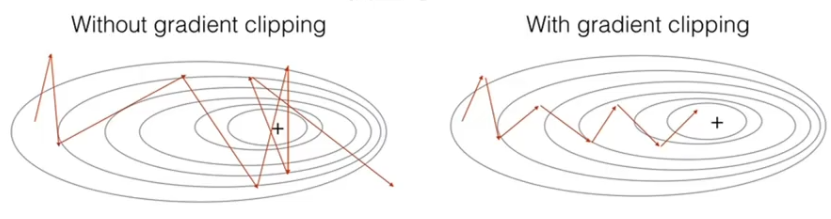
3.5.1、梯度剪切 —— 针对梯度爆炸
????????设置一个梯度剪切闻值,超过则将其强制限制在这个范围之内。
????????
3.5.2、ReLU激活函数
????????
?
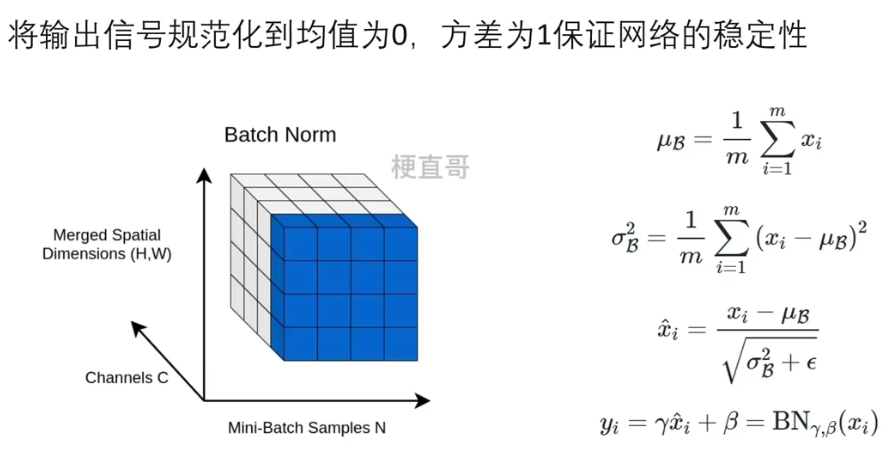
3.5.3、Batchnorm
??????? 对某一个通道进行规范化操作。
????????
?
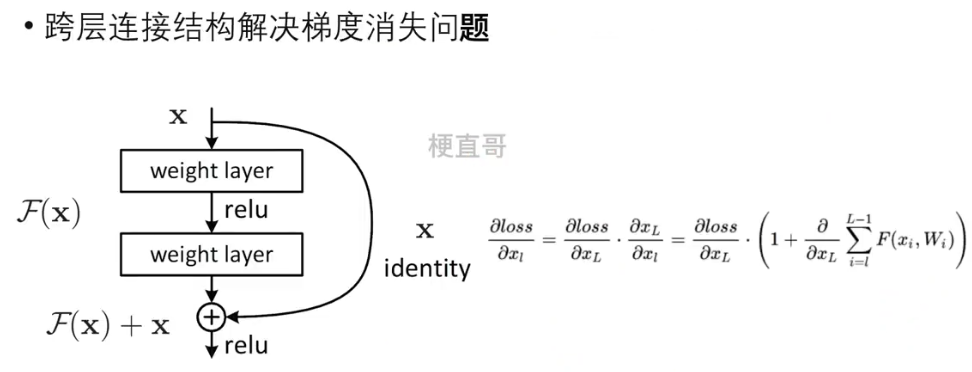
3.5.4、残差结构
?????????
?
?
4、模型文件的读写
?
4.1、张量的保存和加载
import torcha = torch.rand(6)
atensor([0.8608, 0.6997, 0.4133, 0.6113, 0.5393, 0.8223])
torch.save(a,"model/tensor_a")torch.load("model/tensor_a")tensor([0.8608, 0.6997, 0.4133, 0.6113, 0.5393, 0.8223])
a = torch.rand(6)
b = torch.rand(6)
c = torch.rand(6)
[a,b,c][tensor([0.6443, 0.6780, 0.9844, 0.3475, 0.3763, 0.9680]), tensor([0.0351, 0.3652, 0.9474, 0.5658, 0.5001, 0.7580]), tensor([0.5543, 0.2713, 0.3125, 0.0378, 0.0676, 0.2208])]
torch.save([a,b,c],"model/tensor_abc")torch.load("model/tensor_abc")[tensor([0.6443, 0.6780, 0.9844, 0.3475, 0.3763, 0.9680]), tensor([0.0351, 0.3652, 0.9474, 0.5658, 0.5001, 0.7580]), tensor([0.5543, 0.2713, 0.3125, 0.0378, 0.0676, 0.2208])]
tensor_dict= {'a':a,'b':b,'c':c}
tensor_dict{'a': tensor([0.6443, 0.6780, 0.9844, 0.3475, 0.3763, 0.9680]),
'b': tensor([0.0351, 0.3652, 0.9474, 0.5658, 0.5001, 0.7580]),
'c': tensor([0.5543, 0.2713, 0.3125, 0.0378, 0.0676, 0.2208])}
torch.save(tensor_dict,"model/tensor_dict_abc")torch.load("model/tensor_dict_abc"){'a': tensor([0.6443, 0.6780, 0.9844, 0.3475, 0.3763, 0.9680]),
'b': tensor([0.0351, 0.3652, 0.9474, 0.5658, 0.5001, 0.7580]),
'c': tensor([0.5543, 0.2713, 0.3125, 0.0378, 0.0676, 0.2208])}
?
?
4.2、模型的保存与加载
from torchvision import datasets
from torchvision import transforms
import torch.nn as nn
import torch.optim as optim
# 定义 MLP 网络 继承nn.Module
class MLP(nn.Module):
# 初始化方法
# input_size输入数据的维度
# hidden_size 隐藏层的大小
# num_classes 输出分类的数量
def __init__(self, input_size, hidden_size, num_classes):
# 调用父类的初始化方法
super(MLP, self).__init__()
# 定义第1个全连接层
self.fc1 = nn.Linear(input_size, hidden_size)
# 定义激活函数
self.relu = nn.ReLU()
# 定义第2个全连接层
self.fc2 = nn.Linear(hidden_size, hidden_size)
# 定义第3个全连接层
self.fc3 = nn.Linear(hidden_size, num_classes)
# 定义forward函数
# x 输入的数据
def forward(self, x):
# 第一层运算
out = self.fc1(x)
# 将上一步结果送给激活函数
out = self.relu(out)
# 将上一步结果送给fc2
out = self.fc2(out)
# 同样将结果送给激活函数
out = self.relu(out)
# 将上一步结果传递给fc3
out = self.fc3(out)
# 返回结果
return out
# 定义参数
input_size = 28 * 28 # 输入大小
hidden_size = 512 # 隐藏层大小
num_classes = 10 # 输出大小(类别数)
# 初始化MLP
model = MLP(input_size, hidden_size, num_classes)4.2.1、方式1(推荐)
# 保存模型参数
torch.save(model.state_dict(),"model/mlp_state_dict.pth")# 读取保存的模型参数
mlp_state_dict = torch.load("model/mlp_state_dict.pth")
# 新实例化一个MLP模型
model_load = MLP(input_size,hidden_size,num_classes)
# 调用load_state_dict方法 传入读取的参数
model_load.load_state_dict(mlp_state_dict)<All keys matched successfully>
?
4.2.2、方式2
# 保存整个模型
torch.save(model,"model/mlp_model.pth")# 加载整个模型
mlp_load = torch.load("model/mlp_model.pth")?
4.2.3、方式3 : checkpoint(推荐)
# 保存参数
torch.save({
'epoch': epoch,
'model_state_dict': model.state_dict(),
'optimizer_state_dict': optimizer.state_dict(),
'loss': loss,
...
}, PATH)# 加载参数
model = TheModelClass(*args, **kwargs)
optimizer = TheOptimizerClass(*args, **kwargs)
checkpoint = torch.load(PATH)
model.load_state_dict(checkpoint['model_state_dict'])
optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
epoch = checkpoint['epoch']
loss = checkpoint['loss']
model.eval()?
参考
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 在奋斗中提升自我,实现梦想——中国人民大学与加拿大女王大学金融硕士项目
- 码住!10款免费又好用的开源低代码开发平台
- 二叉树的遍历和线索二叉树
- 用通俗易懂的方式讲解:使用 MongoDB 和 Langchain 构建生成型AI聊天机器人
- CentOS 7系统加固详细方案SSH FTP MYSQL加固
- JJJ:python学习笔记2
- 数学的雨伞下:理解世界的乐趣
- hadoop必记知识点(2)
- 安谋科技“周易”NPU与飞桨完成II级兼容性测试,助力实现多样化AI部署
- 又涨了:net的域名铁定涨价