机器学习(十) — 强化学习
Reinforcement learning
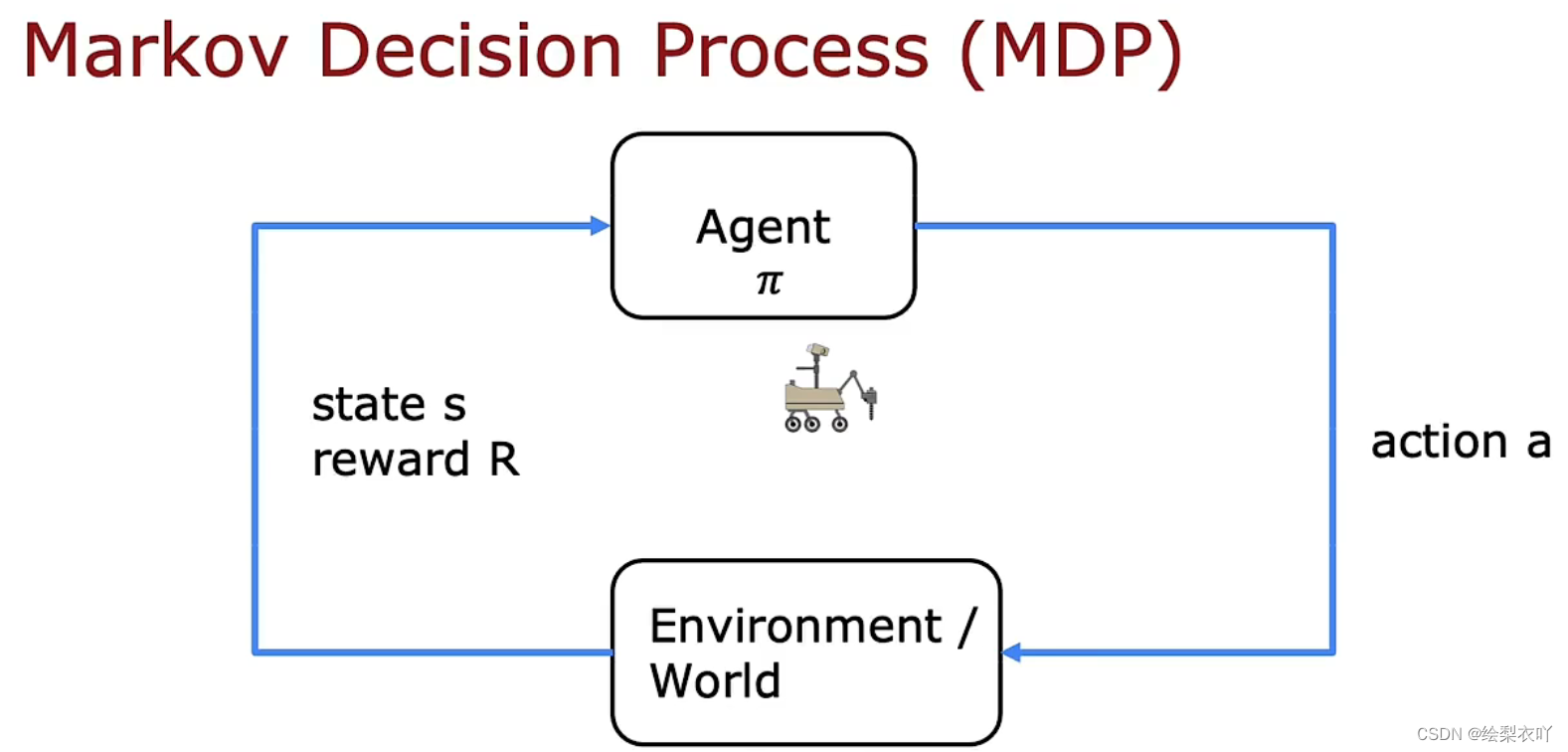
1 key concepts
- states
- actions
- rewards
- discount factor γ \gamma γ
- return
- policy π \pi π
2 return
- definition: the sum of the rewards that the system gets, weighted by the discount factor
- compute:
- R i R_i Ri? : reward of state i
- γ \gamma γ : discount factor(usually close to 1), making the reinforcement learning impatient
r e t u r n = R 1 + γ R 2 + ? + γ n ? 1 R n return = R_1 + \gamma R_2 + \cdots + \gamma^{n-1} R_n return=R1?+γR2?+?+γn?1Rn?
3 policy
policy π \pi π maps state s s s to some action a a a
π ( s ) = a \pi(s) = a π(s)=a
the goal of reinforcement learning is to find a policy π \pi π to map every state s s s to action a a a to maximize the return
4 state action value function
1. definition
$Q(s, a) = $return if
- start in state s s s
- take action a a a once
- behave optimally after that
2. usage
- the best possible return from state s s s is m a x max max Q ( s , a ) Q(s, a) Q(s,a)
- the best possible action in state s s s is the action a a a that gives m a x max max Q ( s , a ) Q(s, a) Q(s,a)
5 bellman equation
s s s : current state
a a a : current action
s ′ s^{'} s′ : state you get to after taking action a a a
a ′ a^{'} a′ : action that you take in state s ′ s^{'} s′
Q ( s , a ) = R ( s ) + γ m a x Q ( s ′ , a ′ ) Q(s, a) = R(s) + \gamma max Q(s^{'}, a^{'}) Q(s,a)=R(s)+γmaxQ(s′,a′)
6 Deep Q-Network
1. definition
use neural network to learn Q ( s , a ) Q(s, a) Q(s,a)
x = ( s , a ) y = R ( s ) + γ m a x Q ( s ′ , a ′ ) f w , b ( x ) ≈ y x = (s, a)\\ y = R(s) + \gamma max Q(s^{'}, a^{'}) \\ f_{w, b}(x) \approx y x=(s,a)y=R(s)+γmaxQ(s′,a′)fw,b?(x)≈y
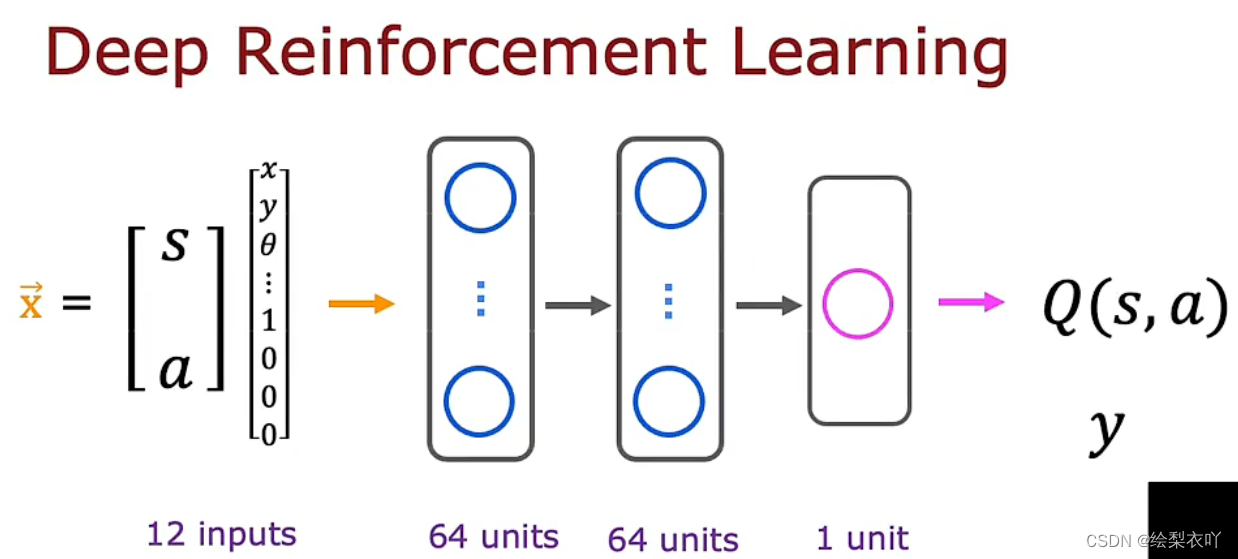
2. step
- initialize neural network randomly as guess of Q ( s , a ) Q(s, a) Q(s,a)
- repeat:
- take actions, get ( s , a , R ( s ) , s ′ ) (s, a, R(s), s^{'}) (s,a,R(s),s′)
- store N most recent ( s , a , R ( s ) , s ′ ) (s, a, R(s), s^{'}) (s,a,R(s),s′) tuples
- train neural network:
- create training set of N examples using x = ( s , a ) x = (s, a) x=(s,a) and y = R ( s ) + γ m a x Q ( s ′ , a ′ ) y = R(s) + \gamma max Q(s^{'}, a^{'}) y=R(s)+γmaxQ(s′,a′)
- train Q n e w Q_{new} Qnew? such that Q n e w ≈ y Q_{new} \approx y Qnew?≈y
- set Q = Q n e w Q = Q_{new} Q=Qnew?
3. optimazation
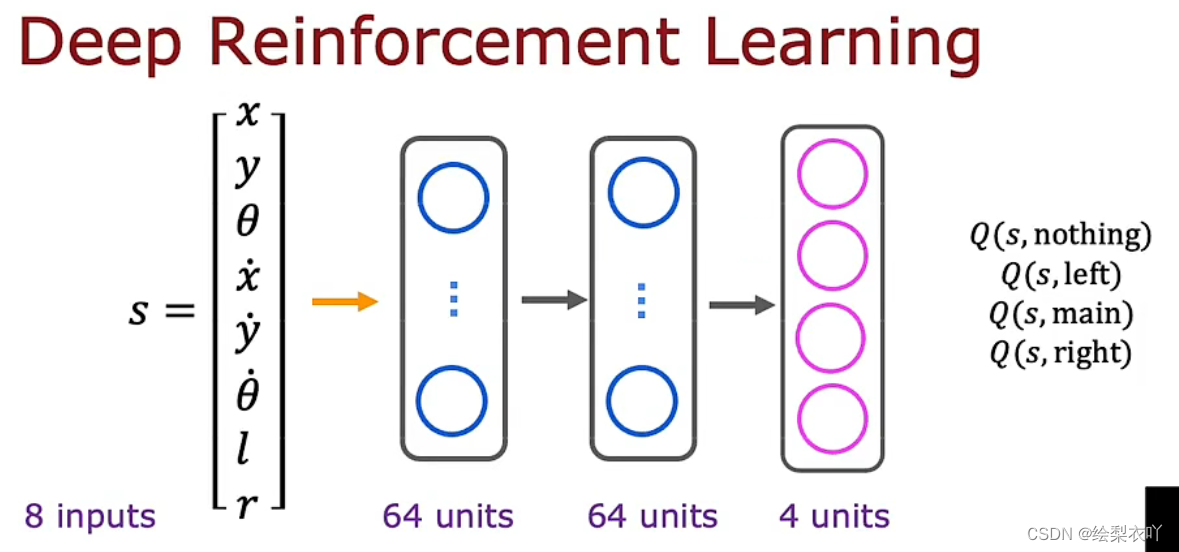
4. ? \epsilon ?-greedy policy
- with probability 1 ? ? 1 - \epsilon 1??, pick the action a a a that maximize Q ( s , a ) Q(s, a) Q(s,a)
- with probability ? \epsilon ?, pick the action a a a randomly
5. mini-batch
use a subset of the dataset on each gradient decent
6. soft update
instead Q = Q n e w Q = Q_{new} Q=Qnew?
w = α w n e w + w b = α b n e w + b w = \alpha w_{new} + w\\ b = \alpha b_{new} + b w=αwnew?+wb=αbnew?+b
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 奇异值分解(SVD)【详细推导证明】
- python学习17
- 特征工程(一)
- 书生·浦语大模型实战营第一次课堂笔记
- 测出Bug就完了?从4个方面教你Bug根因分析!
- .gitignore文件设置了忽略但不生效,git提交过程解析
- AcWing.898.数字三角形(线性DP)
- LeNet-5(fashion-mnist)
- 阿里云 linux Centos7 安装 Miniconda3 + 创建Python环境
- Mediant approximation trick