【动态规划】03斐波那契数列模型_最小花费爬楼梯_C++(easy2)
题目链接:leetcode最小花费爬楼梯
目录
题目解析:

?题目让我们求达到楼梯顶部的最低花费.
由题可得:
?cost[i]?是从楼梯第?i?个台阶向上爬需要支付的费用(每一阶所需的费用由cost[ ]里的值决定)。
可以选择从下标为?0?或下标为?1?的台阶开始爬楼梯,支付费用后,可选择向上爬一个或者两个台阶
那么楼顶在哪?
我们从题目里的实例一来分析:
如果楼顶是i,那么这里的最小花费为应该为10,但是这里输出是15

所以楼顶是在这里:

算法原理:
1.状态表示
先创建一个dp表
首先先思考dp表里面的值所表示的含义(是什么?)
dp[i]表示从i位置到终点的最小花费
这种状态表示怎么来的?
1.经验+题目要求
用之前或者之后的状态,推导出dp[i][j]的值;
根据最近的最近的一步,来划分问题
经验:以i位置为起点,
题目让我们求达到楼梯顶部的最低花费
那么这里我们可以dp[i]来表示。
2.状态转移方程
dp[i]等于什么?
这里我们分两种情况:
第一种情况:
花费i位置(cost[i])后跳一步到i+1位置,再算i+1到楼顶的值;
这里的“算i+1到楼顶的值”就是我们的状态表示,所以这里可以用dp[i+1]来表示;

第二种情况:
花费i位置(cost[i])后跳一步到i+2位置,再算i+2到楼顶的值;
这里的“算i+2到楼顶的值”就是我们的状态表示,所以这里可以用dp[i+2]来表示;
总结一下两种情况:
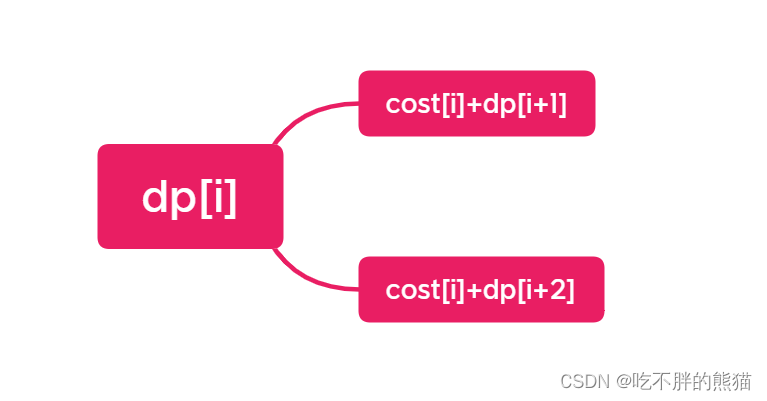
因为我们这里求的是到达楼顶的最小花费,
所以要取这两个情况的最小值:
dp[i]=min(dp[i+1],dp[i+2])+cost[i]
3.初始化
(保证填表的时候不越界)

我们在到达[n-1]与[n-2]时,
达到楼梯顶部的最低花费:
dp[n-1]=cost[n-1];
dp[n-2]=cost[n-2].
4.填表顺序
(为了填写当前状态的时候,所需要的状态已经计算过了)
这里所需要的状态是:dp[i+1],dp[i+2]
是从右往左推的
所以这里填表顺序是从右往左;
5.返回值
(根据题目要求和状态表示)
综上分析:
返回值为:min(dp[0],dp[1]);
编写代码:

class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
//1.创建dp表
//2.初始化
//3.填表
//4.返回结果
int n=cost.size();
vector<int> dp(n);
dp[n-1]=cost[n-1];
dp[n-2]=cost[n-2];
for(int i=n-3;i>=0;i--)
{
dp[i]=min(dp[i+1],dp[i+2])+cost[i];
}
return min(dp[0],dp[1]);
}
};本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【我的RUST库】get_local_info 0.2.2发布
- 【Webpack】模块打包 CommonJS和ES6 Module的区别
- 删除数据后, redis 内存占用还是很高怎么办?
- .pings勒索病毒的威胁:如何应对.pings勒索病毒的突袭?
- 世微AP2121太阳能草坪灯驱动芯片
- C#-特性
- 公司办公电脑文件防泄密系统
- 【Java后端】——JAVA后端学习路线
- UI跟随物体的关键是什么?重要吗?
- 【期末不挂科-单片机考前速过系列P9】(第九章:6题速过单片机概述)经典例题盘点(带图解析)