Codeforces Round 895 (Div. 3)补题

?Two Vessels（Problem - A - Codeforces）

题目大意：有两个无限容器，目前一个容器中有a克水，另一个容器中有b克水，现有一个大小为cg的容器，我们每次可以从一个无限容器中取任意不大于c克的水（未必是整数），将它放进另一个无限容器中，求最多需要转移多少次，两无限容器中的水数目相同。

思路：求出平均数，它们与平均数的差值除于c即可，重点是可能有0.5的情况，所以我们全部定义成double类型，然后除完c，上取整。

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		double a,b,c;
		scanf("%lf%lf%lf",&a,&b,&c);
		double v=(a+b)*1.0/2;
		v=max(b,a)-v;		
		cout<<ceil(v*1.0/c)<<endl;
	}
}

The Corridor or There and Back Again（Problem - B - Codeforces）

题目大意：现有一排房间，初始位置是1，其中有n个房间中有陷阱，但是陷阱只会在我们进入房间后第si秒出发，一旦被触发，这个房间既不能进也不能出，要求从1开始再回到1，最远能走到哪个点。

思路：这里实际上很简单，按照陷阱所在的位置排序，然后遍历，求出再触发这个陷阱后往后走，回来的时候恰好离开这个点能走到哪里，这就是满足这个陷阱的最远距离，所有陷阱的最远距离求min，当然如果当前的最远距离小于访问的陷阱的下标时，就没有讨论的意义了，因为根本走不到这个陷阱，同时后面都大于它，更走不到。

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		int n;
		scanf("%d",&n);
		vector<pair<int,int>>p;
		for(int i=0;i<n;i++)
		{
			int d,s;
			scanf("%d%d",&d,&s);
			p.push_back({d,s});
		}
		sort(p.begin(),p.end());
		int r=0x3f3f3f3f;
		for(auto it:p)
		{
			int d=it.first,s=it.second;
			if(r<d) continue;
			int v=d+(s-1)/2;
			r=min(r,v);
		}
		cout<<r<<endl;
	}
}

Non-coprime Split（Problem - C - Codeforces）

题目大意：给出l<=r,要求l<=a+b<=r使得gcd(a,b)!=1,如果成立就输出a,b,否则输出-1.

思路：本来是想找规律优化的，但是总会出现边界情况，所以最后干脆暴力，就是从l开始循环，到r结束，对每个数去找它的非1非本身的因数，一旦找到一个合法的j，那么a=j,b=j*(i/j-1),然后问题就解决了，两者的gcd至少为j，因为j不等于1，所以一定成立。找不到就-1咯。

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		int l,r;
		scanf("%d%d",&l,&r);
		int a=0,b=0;
		for(int j=l;j<=r;j++)
		{
			int flag=0;
			for(int i=2;i<=j/i;i++)
			{
				if(j%i==0)
				{
					flag=i;
					break;
				}
			}
			if(flag)
			{
			a=flag,b=flag*(j/flag-1);
			break;
			}
		}
		if(a&&b)printf("%d %d\n",a,b);
		else printf("-1\n");
		}
	}

Plus Minus Permutation（Problem - D - Codeforces）

题目大意：现在有一个长度为n的排列，我们可以指定顺序，现有数x和y，要求排列的k*x位(k=1,2,...)的和减去k*y(k=1,2,...)位的和的最大值。

思路：这个题要注意到kx,ky对应的位是会有重合的，重合位置既能整除x，又能整除y，很容易想到通过x*y来找，实际不是的，应该是通过它们的最小公倍数来找，因为x和y之间可能有倍数关系，如果用x*y来找可能会漏掉。它们公倍数的位肯定无意义，因为相减抵消，所以有效的是非公倍数的位，那么就是x还能找到的位从n开始放数，y还能找到的位从1开始放数，求差值，实际上对x放的是从n开始的等差数列，对y放的是从1开始的等差数列，那么求和就解决问题了，主要记得把重合位去掉，以防误算。

#include<bits/stdc++.h>
using namespace std;
#define int long long
signed main()
{
	int t;
	scanf("%lld",&t);
	while(t--)
	{
		int n,a,b;
		scanf("%lld%lld%lld",&n,&a,&b);
		int g=__gcd(a,b);
		g=g*(a/g)*(b/g);
		int x=n/a,y=n/b,z=n/g;
		y-=z,x-=z;
		int ans=(n+n-x+1)*x/2-(1+y)*y/2;		
		printf("%lld\n",ans);
	}
}

Data Structures Fan（Problem - E - Codeforces）

题目大意：现有一个数组a[]和一个字符串s，我们现有两种操作：

(1,l,r）:将s中区间l到r内的数全部与1异或，即0变1，1变0

(2,g):在a[]中找满足条件的的位置，即下标i在s中对应的s[i]==g,求这些位上的异或和。

思路：这题又涉及到区间修改，又涉及到区间查询，所以很容易想到用线段树来做，但是这只是场div3，而且才到E题，还用不了这么高级的数据结构，我们再来看看有没有什么规律，我们最后想要的是什么，想要的只是两个值，我们用x1和x0来表示，而这题的难点在于如何在区间被修改之后更新这两个值，我们来看看修改前后的区别，如果s[i]的这个位置为1，那么在修改之前会出现在x1中，不会出现在x0中，修改之后不会出现在x1中，但会出现在x0中，所以x1的变化是a[i]，x0的变化是a[i],然后这里的a[i]实际上是一段区间。那么我们别的运算可能需要具体知道哪些数需要新增，哪些数需要删掉，但这里是异或运算，我们将x1和x0都异或上这个区间，那么原本有的自然因为跟自己异或变成0，原本没有的自然也会被新增进去，那么不就实现修改了。如何获取一段区间的异或和呢，显然我们可以预处理前缀和，再通过前缀和得到。

这题最核心的地方就是首先要明白我们想要的实际是上就是两个值，然后将区间修改与a[]联系起来，已经找到区间修改后对这两个值的影响，一部分新增一部分去掉，看似麻烦，实际上可以利用异或的性质直接让结果异或这一段区间。

#include<bits/stdc++.h>
using namespace std;
int a[200010],m[200010];
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		int n;
		string s;
		cin>>n;
		for(int i=0;i<n;i++) scanf("%d",&a[i]);
		cin>>s;
		int x0=0,x1=0;
		for(int i=0;i<n;i++) 
		{
			if(s[i]=='0') x0 ^= a[i];
			else x1 ^= a[i];
			if(i)m[i]=m[i-1]^a[i];
			else m[i]=a[i];
		}
		int q;
		scanf("%d",&q);
		while(q--)
		{
			int op;
			scanf("%d",&op);
			if(op==1)
			{
				int l,r;
				scanf("%d%d",&l,&r);
				x0=x0^m[r-1]^m[l-2];
				x1=x1^m[r-1]^m[l-2];
			}
			else
			{
				int x;
				scanf("%d",&x);
				if(x==0) printf("%d ",x0);
				else printf("%d ",x1);
			}
		}
		printf("\n");
	}
}

Selling a Menagerie（Problem - F - Codeforces）

题目大意：现在有n个动物，第i个动物有一个害怕的动物a[i]，它如果在害怕的动物之前出售，那么价值就是2*c[i]，否则就是c[i],现需要求出动物的出售顺序。

思路：这题它们之间即然有相互关系，那么我们考虑建有向图，

如上图，出现重边(两个点相同，方向不同，我们保留大的)，那么显然可以得到若干块，在每一块内按照拓扑排序排列即可，那么这个题就解决了？当然不是，只有有向无环图才有拓扑排序，但是我们能保证有向，未必能保证无环，如下：

?

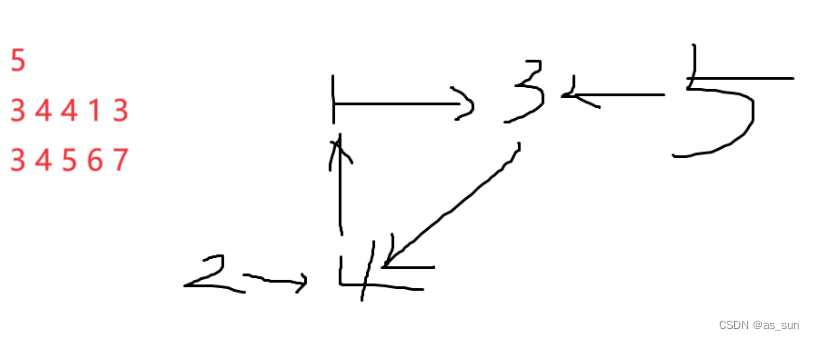这里出现环了，所以它们没有拓扑排序。那怎么办呢，这个问题就很麻烦，似乎就不能从图的角度来考虑了。我们再回到策略本身来看，我们想要使被害怕的动物后输出，为什么它要后输出，因为害怕它的动物能多一倍的价值。所以一个被害怕的动物，害怕它的动物越多，它就输出的越靠后，因为害怕它的需要先输出。那么我们可以将害怕它的动物的价值加起来作为它的权重，权重越大，输出越靠后，每次先输出权重小的，因为它们创造的额外收益最少。当一个动物被输出后，当前的局势就发生变化了，因为在目前的局势下，原本因为它而多了一些权重的动物现在的局面中是没有这些权重的，那么就要将权重值进行修改，然后重新排序。这里我们显然可以用优先队列来实现。

#include<bits/stdc++.h>
using namespace std;
#define int long long
int a[200010],s[200010],c[200010],st[200010];
signed main()
{
	int t;
	scanf("%lld",&t);
	while(t--)
	{
		int n;
		scanf("%lld",&n);
		for(int i=1;i<=n;i++) scanf("%lld",&a[i]),st[i]=0;
		for(int i=1;i<=n;i++)
		{
			scanf("%lld",&c[i]);
			s[a[i]]+=c[i];
		}
		priority_queue< pair<int,int> ,vector< pair<int,int> >,greater< pair<int,int> > >q;

		for(int i=1;i<=n;i++)
		{
			q.push({s[i],i});
		}
		while(q.size())
		{
			auto it=q.top();
			q.pop();
			int i=it.second;
			if(st[i]) continue;
			cout<<i<<" ";
			st[i]=1;
			s[a[i]] -= c[i];
			q.push({s[a[i]],a[i]});
		}
		cout<<endl;
	}
}

这种涉及到决策的问题，没有思路的时候不妨想想我们想要的是什么，我们决策的本质是什么，通过决策的本质来考虑，说不定就能发现一些规律，比如这道题决策的本质是产生额外收益多的后输出，什么时候产生额外收益，那么就是它在害怕它的动物之前输出，它产生的额外收益是多少，就是害怕它的动物的收益总和，而且一个动物被输出后，它带来权重需要被减掉，因为当前的局面发生了变化，在每一个局面下，权重最大和最小的点可能都不同。所以我们要动态的来看，在每个局面中权重最小的肯定是需要先被输出的，因为它被输出，相当于它带的这部分权重会消失，因为如果害怕动物还没输出，它已经输出，那么额外增益肯定没了，我们要最大限度地保证额外增益，所以就要将权重最小的先输出。而且因为动态变化，所以每次先输出的点的权重实际都是0.这里核心在于从拓扑排序考虑出度入度无法解决环，另外额外增益与本身无关，与父节点有关，所以额外增益应该累计在父节点上。