二分查找的数据结构实验报告

一、实验目的：

1、理解二分查找算法的原理及基本思想。

2、学习如何设计并实现二分查找的数据结构实验

二、实验内容（实验题目与说明）

设计一个包含二分查找功能的数据结构实验，并在该实验中调用和测试二分查找算法。通过输入一个待查找的目标元素，程序会输出查找结果，包括目标元素是否找到以及其在数组中的索引，没有目标元素则提示元素不存在。

三、算法设计（核心代码或全部代码）

#include <stdio.h>

int binarySearch(int arr[], int size, int target) {

????int left = 0;

????int right = size - 1;

????while (left <= right) {

????????int mid = left + (right - left) / 2;

????????if (arr[mid] == target) {

????????????return mid; ?// 返回目标元素索引

????????} else if (arr[mid] < target) {

????????????left = mid + 1; ?// 目标元素在右边，更新左边界

????????} else {

????????????right = mid - 1; ?// 目标元素在左边，更新右边界

????????}

????}

????return -1; ?// 目标元素不存在，返回-1

}

?

int main() {

????int arr[] = {2, 3,4,5, 7, 12, 18, 22, 35, 40};

????int size = sizeof(arr) / sizeof(arr[0]);

????int target;

?

????printf("输入要查找的元素: ");

????scanf("%d", &target);

?

????// 查找目标元素

????int result = binarySearch(arr, size, target);

?

????// 输出查找结果

????if (result != -1) {

????????printf("目标元素在索引 %d的位置\n", result);

????} else {

????????printf("这里没有目标元素\n");

????}

?

????return 0;

}

?

四、运行与测试（测试数据和实验结果分析）

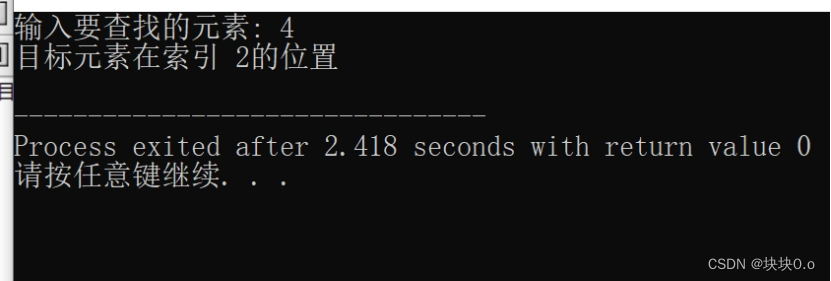
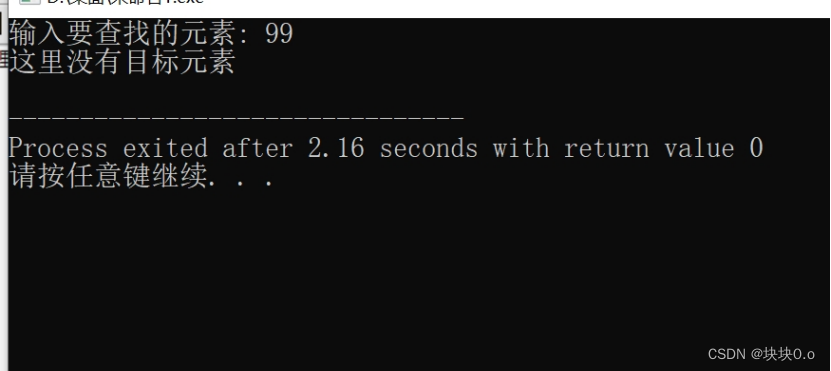
二分查找算法能够高效地在有序数组中查找目标元素。如果目标元素存在于数组中，算法能够准确地找到其在数组中的索引位置。但是二分查找算法要求在进行查找之前，数组必须是有序的。否则，算法无法正常工作。同时，该算法的时间复杂度为 O(logn)，其中 n 是数组的大小。相比线性查找算法的时间复杂度 O(n)，二分查找算法具有更高的效率。

• 总结与心得

通过进行二分查找的数据结构实验，我深刻理解了二分查找算法的原理和实现方法。这种算法利用了数组已经有序的特点，在每次比较后可以将查找范围缩小一半，从而提高查找效率。

?