动态规划—— 求最长不下降序列LIS【集训笔记】

题目描述

设有由n(1≤n≤200)个整数组成的数列，记为:b(1)、b(2)、……、b(n)，若存在i1<i2<i3<…<ie 且有b(i1)<b(i2)<…<b(ie)则称为长度为e的不下降序列。程序要求，当原数列出之后，求出最长的不下降序列。

例如13，7，9，16，38，24，37，18，44，19，21，22，63，15。

例中13，16，18，19，21，22，63就是一个长度为7的不下降序列，同时也有7 ，9，16，18，19，21，22，63组成的长度为8的不下降序列。
?

输入

第一行为n,第二行为用空格隔开的n个整数。

输出

第一行为输出最大个数max(形式见样例)；
第二行为max个整数形成的不下降序列,答案可能不唯一，输出一种就可以了，本题进行特殊评测。

样例输入1

14
13?7?9?16?38?24?37?18?44?19?21?22?63?15

样例输出1

max=8
7?9?16?18?19?21?22?63

提示/说明

无

标签

普及 其他 线性dp LIS

分析：

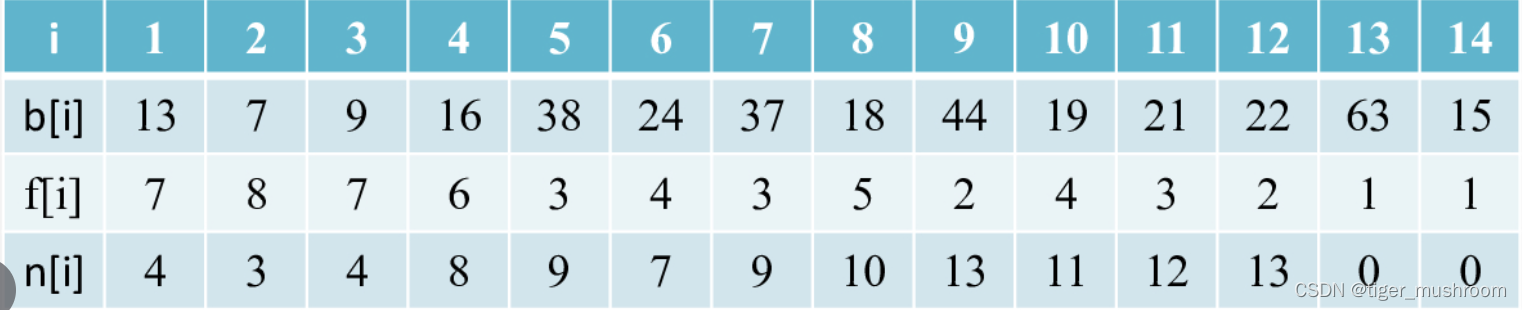
代码：

#include<iostream>
using namespace std;
int n1;
int a[1005],f[1005],n[1005];
void print_lis(int x){
	if(x==0){
		return;
	}
	cout<<a[x]<<" ";
	print_lis(n[x]);
	return;
}
int main()
{
	cin>>n1;
	for(int i=1; i<=n1; i++)
		{
			cin>>a[i];
			f[i]=1;
		}
	for(int i=n1-1; i>=1; i--)
		{
			for(int j=i+1; j<=n1; j++)
				{
					if(a[i]<a[j])
						{
							if(f[i]<f[j]+1)
								{
									f[i]=f[j]+1;
									n[i]=j;
								}
						}
				}
		}
	int max=1;
	for(int i=2; i<=n1; i++)
		{
			if(f[i]>f[max])
				{
					max=i;
				}
		}
	cout<<"max="<<f[max]<<'\n';
	print_lis(max);
	return 0;
}