【深度学习：Few-shot learning】理解深入小样本学习中的孪生网络

备注：本篇博客中有部分图片由GPT生成

深入理解孪生网络：架构、应用与未来展望

在人工智能和机器学习的领域中，**孪生网络（Siamese Network）**已成为一种重要的神经网络架构。这种网络以其独特的方式处理相似性比较任务而闻名，例如在面部识别、签名验证和图像匹配中。在这篇博客中，我们将深入探讨孪生网络的工作原理、主要应用和潜在的未来发展方向。

小样本学习的诞生

人类本身能够通过极少数的样本识别一个新物体，可以凭借动物图册上的各种图片记住不同的动物。在人类的快速学习能力的启发下，研究员希望机器学习模型在学习； 一定类型的大量数据后，对于新的类型，只需要少量的样本就可以快速学习，这就是Few-shot Learning要解决的问题。

Few-shot Learning 是Meta Learning在监督学习领域的应用。Meta Learning，又称为learning to learn，该算法旨在让模型学会“学习”，能够处理类型相似的任务，而不是只会单一的分类任务。

元学习

Meta Learning （元学习）中，在 meta training 阶段将数据集分解为不同的 meta task，去学习类别变化的情况下模型的泛化能力，在 meta testing 阶段，面对全新的类别，不需要变动已有的模型，就可以完成分类。

也就是说，few-shot的训练集中包含了很多的类别，每个类别中有多个样本。在训练阶段，会在训练集中随机抽取C个类别，每个类别含K个样本（总共CK 个数据），构建一个 meta-task，作为模型的支撑集（support set）输入；再从这 C个类别中剩余的数据中抽取一批（batch）样本作为模型的预测对象（batch set）。即要求模型从CK个数据中学会如何区分这C个类别，这样的任务被称为 C-way K-shot 问题。

小样本学习

Few-shot Learning指从少量标注样本中进行学习的一种思想。Few-shot Learning与标准的监督学习不同，由于训练数据太少，所以不能让模型去“认识”图片，再泛化到测试集中。而是让模型来区分两个图片的相似性。当把Few-shot Learning运用到分类问题上时，就可以称之为Few-shot Classification，当运用于回归问题上时，就可以称之为Few-shot Regression。下面提到的Few-shot Learning主要针对分类问题进行讨论。

孪生网络的基本概念

孪生网络（Siamese Network）是一类神经网络结构，它是由两个或更多个完全相同的网络组成的。孪生网络通常被用于解决基于相似度比较的任务，例如人脸识别、语音识别、目标跟踪等问题。

孪生网络的基本思想是将输入数据同时输入到两个完全相同的神经网络中，这两个网络共享相同的权重和参数。通过学习输入数据在这两个网络中的表示，孪生网络可以计算出两个输入样本之间的相似度。处理过程如下：

1. 将两个输入样本通过各自的神经网络得到两个表示向量。
2. 使用一种度量方法（例如欧氏距离、余弦相似度等）计算这两个向量之间的相似度得分。
3. 根据相似度得分进行分类或回归等操作。

孪生网络的细节

训练一个孪生网络首先要有一个大的分类数据集，数据有标注，每一类下面有很多的样本。比如下面的数据集有5类，分别是哈士奇，大象，老虎，鹦鹉，汽车。

基于这个训练集，我们要构造正样本（Positive Samples）和负样本（Negative Samples）。正样本可以告诉神经网络哪些事物是同一类，负样本可以告诉神经网络事物之间的区别。给正样本打上标签1表示同一类，负样本打上标签0表示不同类。如下图所示，这些样本都是从上面的分类数据集里随机抽样出来的。

然后我们可以搭一个神经网络来提取特征（比如做两次卷积），最后得到特征向量$f(x)$

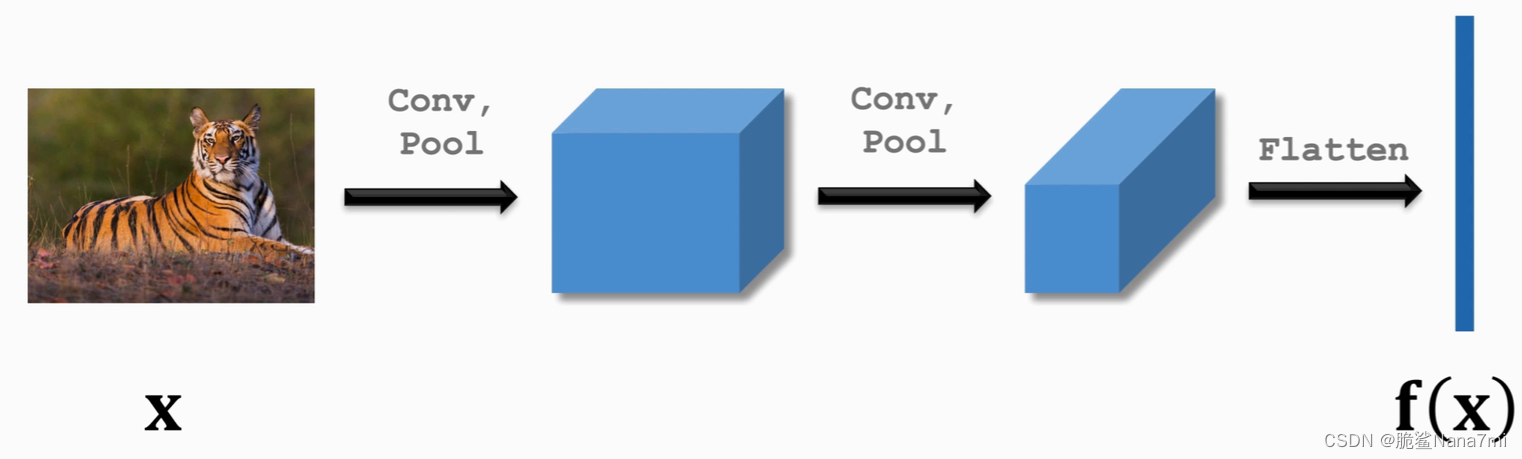
将输入的$x_1$和$x_2$送入我们搭建的神经网络$f(?)$，得到特征向量$h_1$和$h_2$；然后将这两个向量相减再求绝对值，得到向量$z=|h_1?h_2|$，表示这两个向量之间的区别；再通过一个或一些全连接层，最后用Sigmoid激活函数将值映射到0到1之间。

这个最终的输出$sim(x_1,x_2)$就可以用来衡量两个图片之间的相似度（Similarity）。如果两个图片相似，输出应该接近1；如果不同，则应该接近0。

上面提到过样本是有标签的，1表示同一类，0表示不同类。结合标签和刚才的输出$sim(x_1,x_2)$就能选择一个损失函数Loss来计算损失，接着就是老一套的梯度下降和反向传播。反向传播首先更新全连接层的参数，然后进一步传播到卷积层的参数，如下图所示。

通过不断的迭代，最终得到一个效果较好的网络。通过这个网络，我们就可以让机器具有对比事物的能力，为后续的小样本学习奠定基础。

One-shot 预测
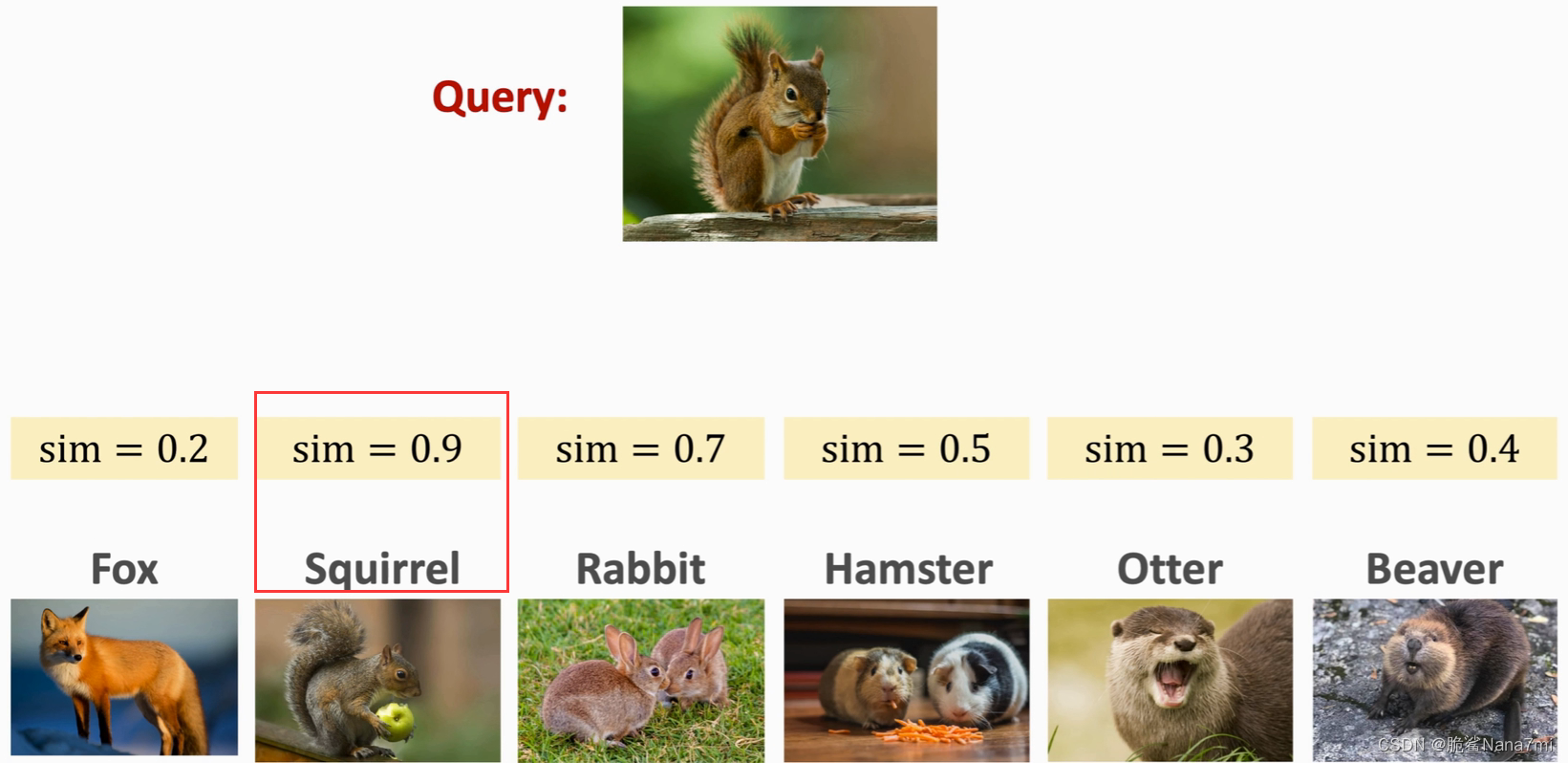
首先需要提供 Support Set ，注意Support Set里出现的图片不在训练集里，然后提供Query，Query应该是Support Set中的某一类，然后Query 与 Support Set 逐一进行对比计算相似度，选取相似度最大的作为预测结果

Triplet Loss

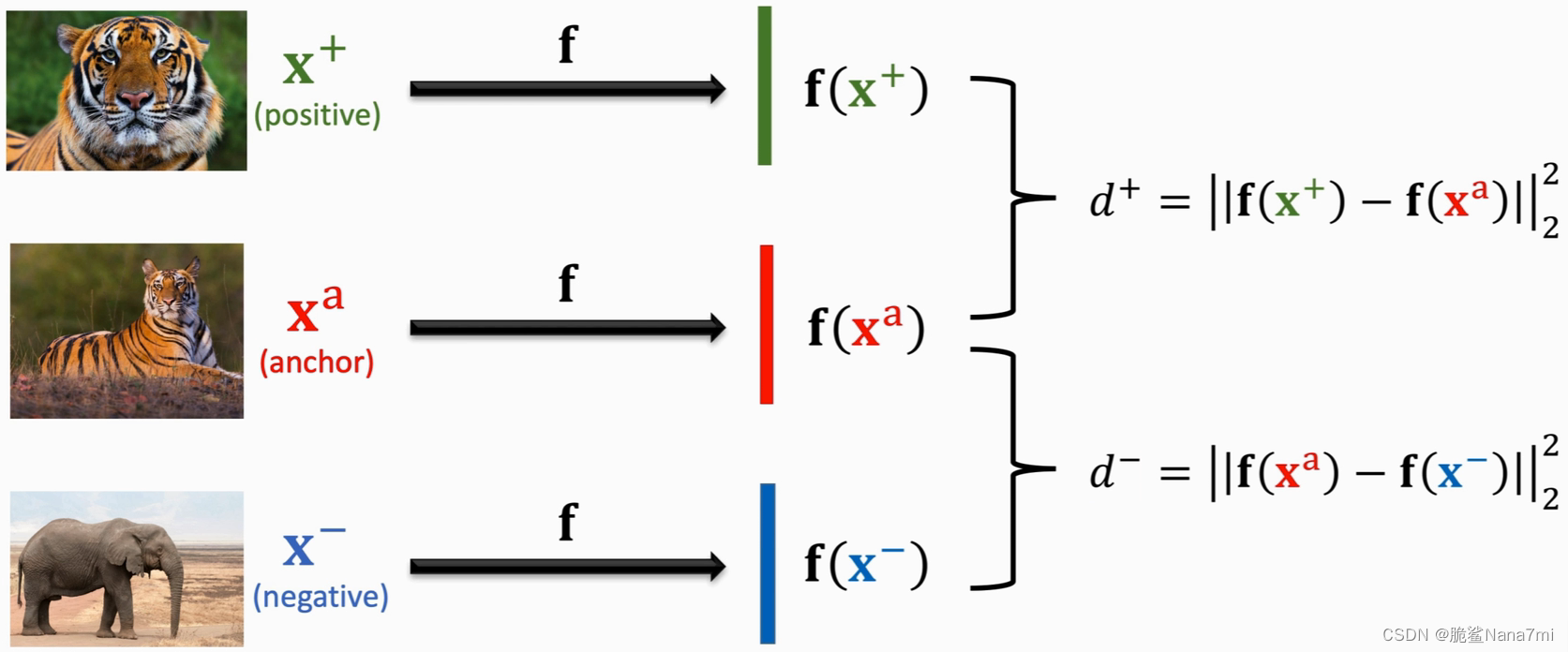
Triplet Loss是另一种训练Siamese Network的方法。它也需要有和上面一样的分类数据集。基于这个数据集，我们需要构造一个三元组。从数据集里随机选取一个图片作为锚点$x^a$（anchor），然后在和它相同类别的数据中随机选一个不同的图片作为正样本$x^{+}$（positive），在不同类别的数据中随机选一个作为负样本$x^{?}$（negative）。

和前面一种方法一样，得到三元组的样本之后也通过一个神经网络提取特征，分别得到特征向量$f(x^{+}),f(x^a),f(x^{?})$。然后分别计算正样本和负样本与锚点之间的距离（二范数的平方），得到$d^{+}$ 和$d^{?}$ 。整个过程如下图所示。

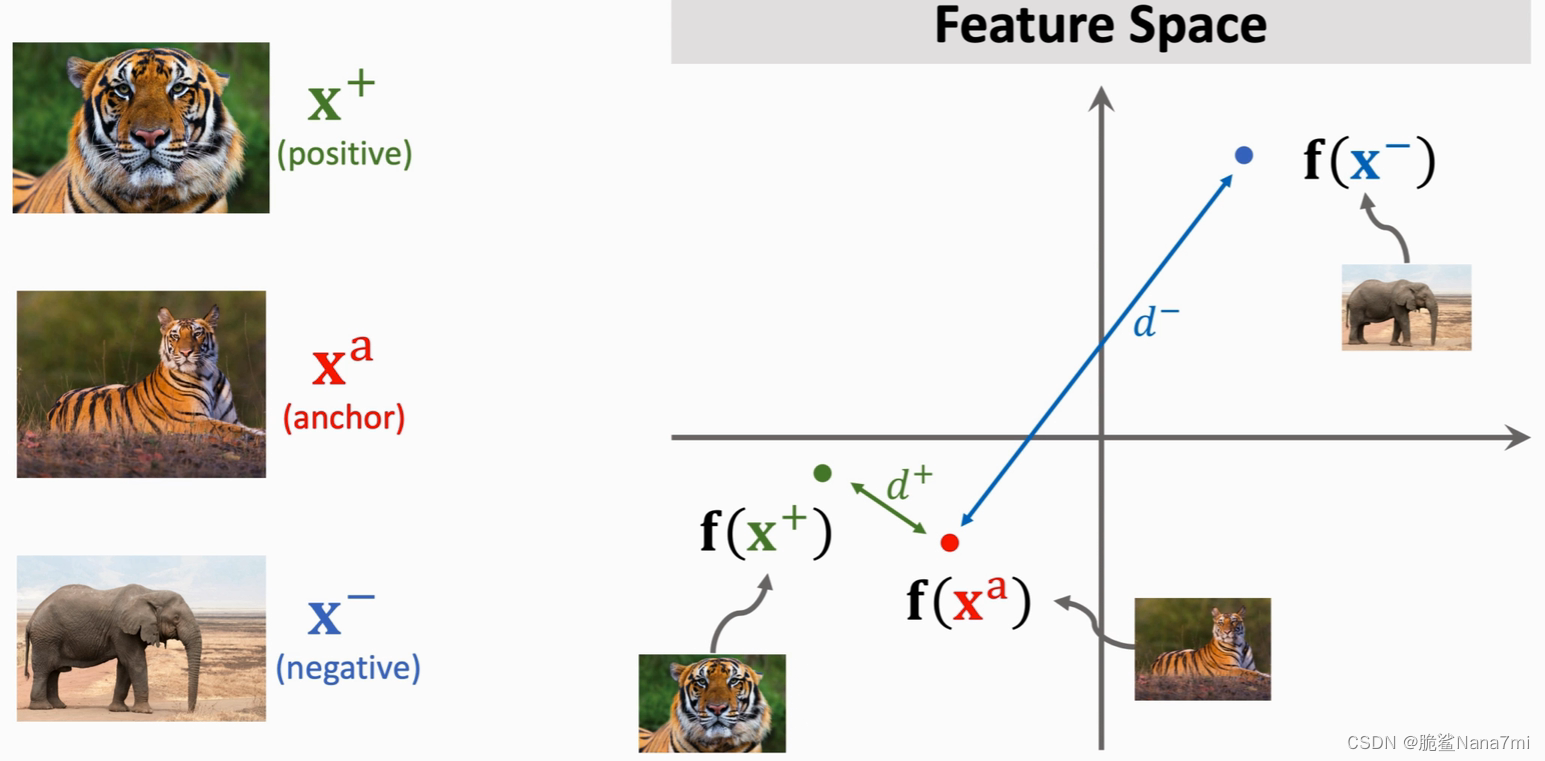
由于正样本和锚点是同一类，所以$d^{+}$应该小；负样本和锚点是不同类，$d^{?}$应该大。并且$d^{+}$要尽可能小，$d^{?}$ 要尽可能大，使得他们容易区分。呈现在特征空间里就是下面这个样子。

损失函数

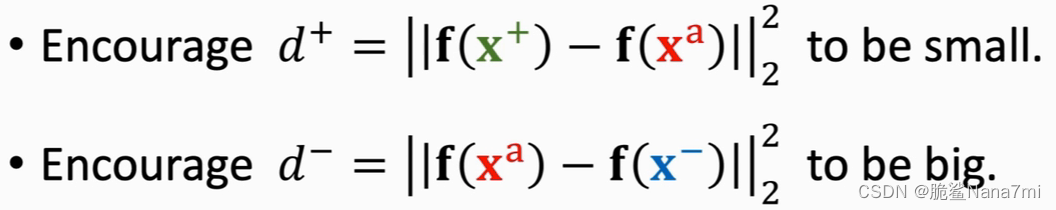
loss为零的情况：$(d^{?})?(d^{+})>=\alpha$ (α是我们设置的超参数) ，说明此时网络能区分正负样本

loss不为零的情况：若不满足上述 $(d^{?})?(d^{+})>=\alpha$ 条件，则令 $loss=(d^{+})+\alpha ?(d?)$ , 在优化过程中，我们希望loss越小越好，此时就会朝着 $d^{+}$ 变小且 $d^{?}$ 变大的方向优化，那么就会使得同一样本距离越来越小，不同样本越来越大


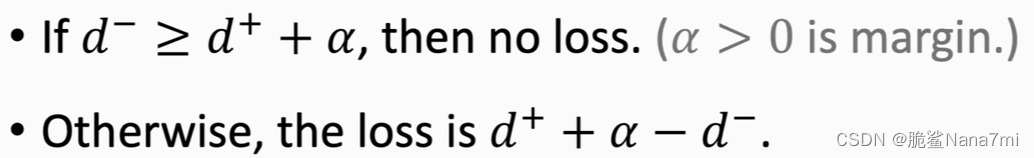
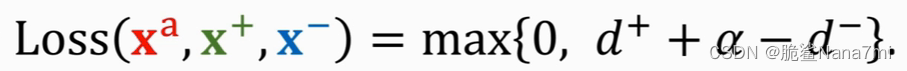
测试
由上述方法得到的神经网络，最终输出为 $d^{+}$和$d^{?}$ ，我们此时将 Query输入网络，得到dist，找出最小的那个dist即可

架构特点

• 参数共享：孪生网络的子网络共享相同的权重，这意味着对于所有输入，都是通过相同的权重和参数来处理的。这不仅减少了模型的参数总数，还帮助网络学习更一致的特征表示。
• 相似性学习：孪生网络的核心任务是学习输入之间的相似性。这通常通过比较特征表示来实现，例如使用欧几里得距离或余弦相似度。
• 灵活性：尽管孪生网络最常用于成对的数据，但它们也可以扩展到处理多个并行输入的复杂任务。

关键组件

• 输入层： 接收原始数据（如图像、文本等）。
• 特征提取层： 通常是一系列卷积层，用于提取输入数据的特征。
• 最后的全连接层： 生成最终的特征表示，用于比较。

训练过程

在训练过程中，孪生网络通过最小化一个特殊的损失函数（例如对比损失）来学习。这个损失函数鼓励网络学习使得相似输入的特征表示接近，而不相似输入的特征表示远离。

主要应用领域

孪生网络在许多领域都有广泛应用，其中包括：

• 面部识别：通过比较不同图像中的面部特征，孪生网络可以用于验证身份。
• 签名验证：孪生网络可以用来比较手写签名的相似性，以验证签名的真实性。
• 图像匹配：在计算机视觉中，孪生网络可以用来识别不同图像中相似的对象或场景。

未来展望

随着技术的进步，孪生网络可能会在以下方面有新的发展：

• 多模态学习：结合不同类型的数据（如文本、图像和声音），孪生网络可以用于更复杂的比较任务。
• 强化学习的集成：孪生网络可以与强化学习结合，以在动态环境中进行更有效的决策。
• 自适应学习：通过持续学习和适应新数据，孪生网络可以在变化的环境中保持其效能。

示例图片

为了更好地解释孪生网络的概念，我将生成一些示例图片：

1. 两张面孔图片，展示如何通过孪生网络进行比较。
2. 两个签名的例子，说明孪生网络在签名验证中的应用。
3. 一个物体在连续视频帧中的图片，演示物体追踪的过程。 这些示例图片将有助于理解孪生网络在实际应用中的工作方式。

面部识别示例
生成一个示例，展示两张面部图片，旁边标注“相似”或“不相似”，以展示孪生网络如何进行面部识别比较。

上图展示了一个面部识别的示例，用于说明孪生网络如何比较两张面部图像来判断它们是否相似。

签名验证示例
接下来，我将生成一个关于签名验证的示例图像。这个图像将展示两个签名，旁边标注“相似”或“不相似”，以展示孪生网络在签名验证中的应用。

上图展示了签名验证的示例，用于说明孪生网络如何比较两个签名以判断它们是否相似。

物体追踪示例
最后，我将生成一个关于物体追踪的示例图像。这个图像将展示一个物体在连续视频帧中的不同位置，以展示孪生网络在物体追踪中的应用。

结论

孪生网络作为一种强大的机器学习工具，在众多领域展现了其独特的价值。随着研究的深入和技术的发展，我们期待看到孪生网络在未来解决更多复杂和挑战性的问题。