7.10非递减子序列(LC491-M)
发布时间:2023年12月31日
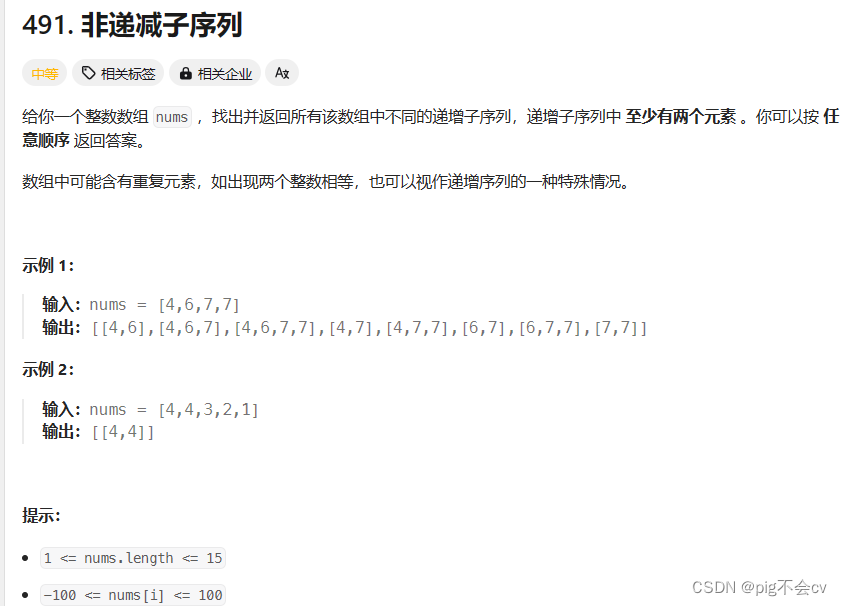
算法:
在90.子集II?(opens new window)中我们是通过排序,再去重来达到去重的目的。
而本题求自增子序列,是不能对原数组进行排序的,排完序的数组都是自增子序列了。
肯定还是回溯算法。
画树:

树里面其实有两个注意点:
(1)每个子集中,所取元素应该大于等于前一个元素
(2)同一层树下,不能取重复的元素来制作子集
回溯三部曲:
1.确定返回值和参数
返回值:void
参数:
int[] nums(题目给出)
int startIndex:需要startIndex,调整下一层递归的起始位置。
2.确定终止条件
本题其实类似求子集问题,也是要遍历树形结构找每一个节点,所以和回溯算法:求子集问题!?(opens new window)一样,可以不加终止条件(求子集时为了便于理解,终止条件是startindex >= nums.length,但其实这个终止条件可以不加),startIndex每次都会加1,并不会无限递归。
但本题收集结果有所不同,题目要求递增子序列大小至少为2。
if (path.length > 1) {
result.add(path);
// 注意这里不要加return,因为要取树上的所有节点
}3.单层递归逻辑
其实就是注意点,当出现以下情况时,continue,跳出for循环
(1)每个子集中,所取元素应该大于等于前一个元素
(2)同一层树下,不能取重复的元素来制作子集
具体实现时,要用一个数组来进行去重操作,题目说数值范围[-100, 100]
将用过的值插入数组,表示这个元素在本层用过了,本层后面不能再用了
(为什么用数组?
若用集合,程序运行的时候对集合频繁的insert,集合需要做哈希映射(也就是把key通过hash function映射为唯一的哈希值)相对费时间,而且每次重新定义set,insert的时候其底层的符号表也要做相应的扩充,也是费事的。)
把nums[i]加入path
递归
回溯:把刚刚加入的nums[i]弹出
调试过程
第一次调试:
class Solution {
//两个全局变量
List<List<Integer>> result = new LinkedList<>();
List<Integer> path = new LinkedList<>();
public List<List<Integer>> findSubsequences(int[] nums) {
backtracking(nums, 0);
return result;
}
void backtracking (int[] nums, int startindex) {
//确定终止条件,收集结果
if (startindex >= nums.length) {
result.add (new LinkedList(path));
return;
}
//单层递归逻辑
for (int i=startindex; i <= nums.length; i++){
//题目中说:-100 <= nums[i] <= 100,说明nums的最大长度为201
//为了确保所有数字都能被记录,去重数组的长度被设置为 201
int[] used = new int[201];
/*跳出循环的条件:
(1)nums[i]<当前path中的最后一个值,前提是path非空
注意:这里不是nums[i]<nums[i-1],因为nums本身无序,而path有序
(2)nums[i]的值和该层前面的值重复了:
每用过一次,就让该值在used中对应索引的位置(used[nums[i]+100]==1)为1,
因为-100 <= nums[i] <= 100,为了得到合法的索引(>=0),used中nums对应的索引为used[nums[i]+100]
若在循环中发现used中该值为1,说明重复了
*/
if (!path.emphty() && nums[i]<path.get(path.size()-1) || used[nums[i]+100]==1) continue;
used[nums[i]+100]=1;//标记用过的值
path.add(nums[i]);
//递归
backtracking(nums, i+1);
//回溯
path.removeLast();
}
}
}
原因:
java中判断(is)非空(Empty)的函数为:isEmpty()
isEmpty()我写得不对。
另外,used数组是记录每层是否使用重复元素的,应该放在for循环外面
第二次调试:

原因:
问题在终止条件上,索引是从0-nums.length-1,
????????所以for循环终止条件应该为?i <?nums.length
另外,
????????收集结果时不要return,因为要取树上的所有节点,而不是叶子节点
正确代码:
class Solution {
//两个全局变量
List<List<Integer>> result = new LinkedList<>();
List<Integer> path = new LinkedList<>();
public List<List<Integer>> findSubsequences(int[] nums) {
backtracking(nums, 0);
return result;
}
void backtracking (int[] nums, int startindex) {
//确定终止条件,收集结果
if (path.size() > 1) {
result.add (new LinkedList(path));
}
//单层递归逻辑
//题目中说:-100 <= nums[i] <= 100,说明nums的最大长度为201
//为了确保所有数字都能被记录,去重数组的长度被设置为 201
int[] used = new int[201];
for (int i=startindex; i < nums.length; i++){
/*跳出循环的条件:
(1)nums[i]<当前path中的最后一个值,前提是path非空
注意:这里不是nums[i]<nums[i-1],因为nums本身无序,而path有序
(2)nums[i]的值和该层前面的值重复了:
每用过一次,就让该值在used中对应索引的位置(used[nums[i]+100]==1)为1,
因为-100 <= nums[i] <= 100,为了得到合法的索引(>=0),used中nums对应的索引为used[nums[i]+100]
若在循环中发现used中该值为1,说明重复了
*/
if (!path.isEmpty() && nums[i] < path.get(path.size()-1) || used[nums[i]+100]==1) continue;
used[nums[i]+100]=1;//标记用过的值
path.add(nums[i]);
//递归
backtracking(nums, i+1);
//回溯
path.removeLast();
}
}
}时间空间复杂度:

文章来源:https://blog.csdn.net/m0_50696252/article/details/135314941
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- SPI相关通信--看懂这篇就够, test later
- SCPMA最新研究论文推荐!中国移动&玻色量子发布联合研究成果
- 有没有什么软件可以用来线上走审批流程的?
- C++/CLI——1简介
- 李沐-《动手学深度学习-02-目标检测
- C&C++逻辑运算符
- 嵌入式(八)电源低功耗管理 | 五种运行模式 模式转换 睡眠定时器唤醒
- Farewell to Pika, Embracing the Arrival of PikiwiDB in 2024
- rotate-captcha-crack项目重新训练百度旋转验证码角度预测模型
- briefly describe the classic sorting algorithm