【算法每日一练]-练习篇 #Tile Pattern #Swapping Puzzle # socks

目录

?今日知识点：

二维前缀和

逆序对

袜子配对(感觉挺难的，又不知道说啥)? ??

Tile Pattern

Swapping Puzzle?

socks

---

????????

????????

Tile Pattern

331

题意：有一个10^9*10^9的方格。W表示白色方格，B表示黑色方格。每个(i,j)方的颜色由(i%n,j%n) 决定。我们给出n*n的字符阵列。进行q此查询。每次输入两个坐标，找出矩形区域内的黑色方格数量。

输入：

样例解释：?

?

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1024;
int n,dp[N][N];

ll f(int x,int y){
	ll ret=1ll*(x/n)*(y/n)*dp[n][n];//先计算完整的块，左上角
	ret+=dp[x%n][y%n];//右下角
	ret+=1ll*dp[x%n][n]*(y/n);//左下角
	ret+=1ll*dp[n][y%n]*(x/n);//右上角
	return ret;
}
int main(){
	int q;
	cin>>n>>q;
	char p[N][N];
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){//从(1,1)开始初始化
			cin>>p[i][j];
			dp[i][j]=(p[i][j]=='B')+dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1];
		}
	}
	while(q--){
		int a,b,c,d;
		cin>>a>>b>>c>>d;
		c++;d++;
		cout<<f(c,d)-f(a,d)-f(c,b)+f(a,b)<<'\n';
	}
}

????????

?????????

?????????

Swapping Puzzle?

332D

题意：给你两个h*w的数字阵列，问是否可以经过以下操作将第一个阵列变成第二个阵列，如果可以输出最小操作次数，如果不能输出-1.

操作1：交换相邻的两行

操作2：交换相邻的两列

思路:

其实交换的本质就是把列号和行号交换了，目前阵列对应的行号如下图所示。

那么很明显，如果这个行号和列号是完全正确的，那么a2[1][2]等于a1[1][3]，a2[2][1]等于a1[3][1]，你发现只要a2的逻辑坐标和a1的逻辑值的坐标对应数字一样，那么这个行列号就是正确的。那么行列号完全可以直接暴力枚举并存起来的。然后进行判断，看看这个行列号是否和目标阵列的相符合。最后求最少得交换次数，就是求逆序对数即可（之前讲过这个问题）。

?????????

#include <bits/stdc++.h>
using namespace std;
int a1[6][6],a2[6][6],b1[250][6],b2[250][6];
int h,w,tot1,tot2,vis[10],tmp[10];

void dfs1(int k){
	if(k>h){
		memcpy(b1[++tot1],tmp,sizeof(tmp));
		return ;
	}
	for(int i=1;i<=h;i++){
		if(vis[i])continue;
		vis[i]=1;tmp[k]=i;
		dfs1(k+1);
		vis[i]=0;
	}
}
void dfs2(int k){
	if(k>w){
		memcpy(b2[++tot2],tmp,sizeof(tmp));
		return ;
	}
	for(int i=1;i<=w;i++){
		if(vis[i])continue;
		vis[i]=1;tmp[k]=i;
		dfs2(k+1);
		vis[i]=0;
	}
}
bool check(int k1,int k2){
	int i=1,j=1;
	while(1){
		if(a1[b1[k1][i]][b2[k2][j]]==a2[i][j])j++;//看看逻辑位置和实际位置的数字是否一样
		else return 0;
		if(j==w+1)i++,j=1;
		if(i>h)return 1;
	}
}
int main(){
	cin>>h>>w;
	for(int i=1;i<=h;i++)
	for(int j=1;j<=w;j++){
		cin>>a1[i][j];//输入原始阵列
	}
	for(int i=1;i<=h;i++)
	for(int j=1;j<=w;j++){
		cin>>a2[i][j];//输入目标阵列
	}
	int f=0;
	for(int i=1;i<=h;i++)//特判
	for(int j=1;j<=w;j++)
		if(a1[i][j]!=a2[i][j]){f=1;break;
		}
	if(f==0){cout<<0;return 0;
	}
    //预处理两行数字的全排列
	memset(vis,0,sizeof(vis));
	dfs1(1);
	memset(vis,0,sizeof(vis));
	dfs2(1);
    //进行行和列的匹配
	int ans=1e8;
	for(int i=1;i<=tot1;i++)
	for(int j=1;j<=tot2;j++){
		if(check(i,j)){//看看是否匹配
			int an=0;
			for(int p=1;p<=h-1;p++){
				int t=p+1;
				while(t<=h){//统计逆序对数
					if(b1[i][p]>b1[i][t])an++;
					t++;
				}	  
			}
			for(int p=1;p<=w-1;p++){
				int t=p+1;
				while(t<=w){
					if(b2[j][p]>b2[j][t])an++;
					t++;
				}	  
			}
			if(an)ans=min(ans,an);//如果方案更新了，更新最优答案
		}
		
	}
	if(ans!=1e8)cout<<ans;//输出答案
	else cout<<-1;
}

?????????

????????

socks

334C

题意：一共有n对袜子第i对颜色都是i。但是不小心丢了k只，每只颜色是a1,a2……ak，我们打算把剩下的2n-k只袜子组成[(2n-k)/2]对。每对袜子的奇怪程度是|i-j|（i，j是两个袜子的颜色）。问袜子的奇怪程度和最小是多少？（注意袜子可能有剩余，剩余的袜子不穿所以没有奇怪程度）

(1<k<n<2*10^5)

输入：? ? ?输出：2

4 2
1 3

样例解释：现在仅剩下1,2,2,3,4,4，然后?(1,2),(2,3),(4,4)? 对应奇怪程度和∣1?2∣+∣2?3∣+∣4?4∣=2

思路：

主要思路就是贪心。我们可以将袜子给从小到大进行排序。然后注意到对于1,2,2,3无论是(1,2)(2,3)还是(1,3)(2,2)都是一样的（可以理解成一条线段分成了两端）。也就是说同色的袜子我们放在一起才是最优的。

那么就只需要处理剩余的k个袜子就行了。如果说k是偶数就很好做，直接前后两两组合就行。

如果k是奇数，就要考虑丢掉某一个袜子。丢掉的袜子一定可以使得最终的奇怪程度最小。那么也就是我们要暴力尝试丢掉每一只袜子试试 。但是O(n^2)万万不行。

好，下面就有点玄学了。首先丢掉的袜子一定是奇数的位置。

如图：

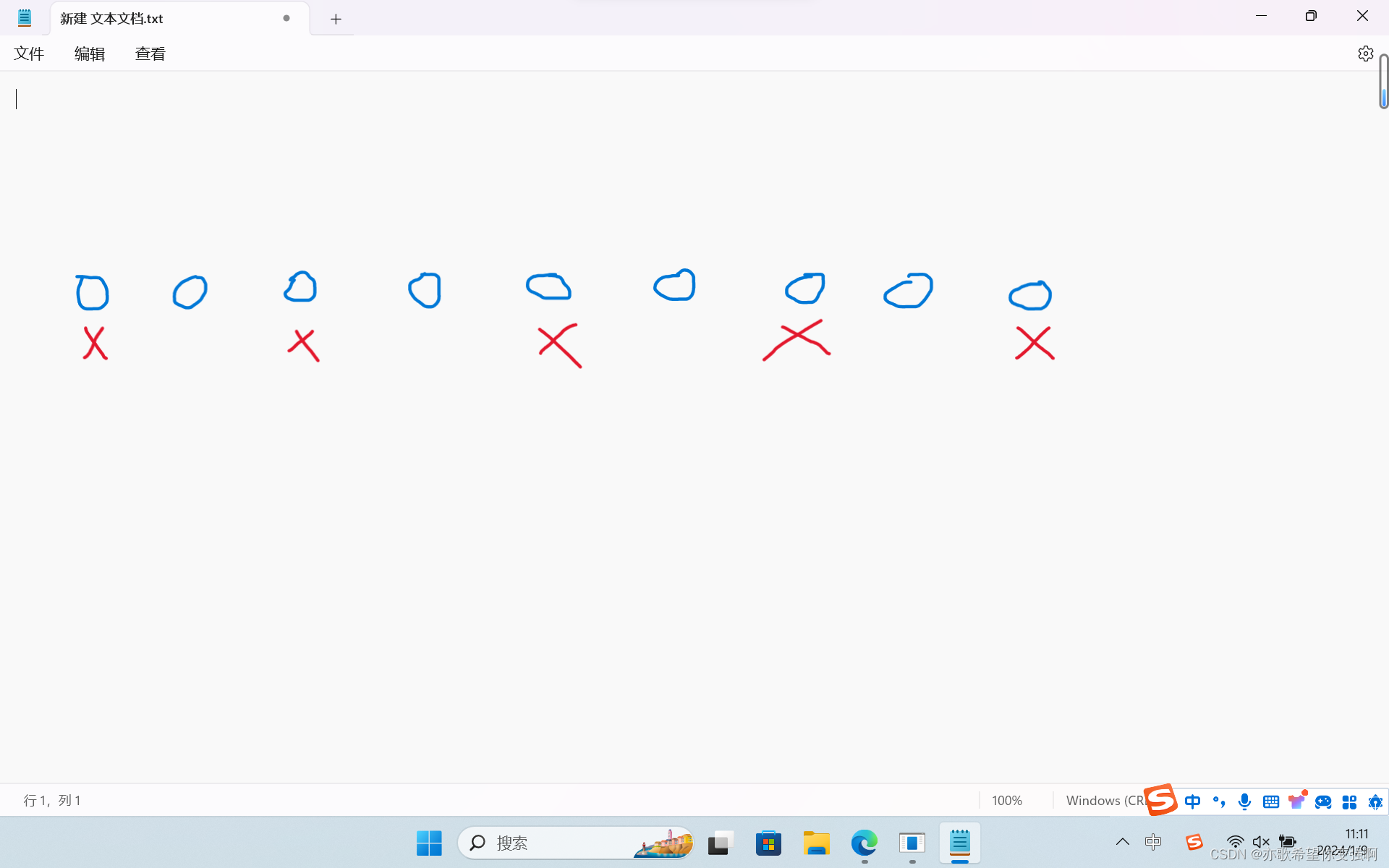
因为偶数的位置一定刚好可以和前面的奇数位置匹配，如果丢掉偶数的位置，前面的位置必然有一个多出来的，然后只能和后面的匹配，那么奇怪程度必然会更大，这一定不是最优解。

只有丢掉奇数位置，因为前面和后面都是偶数个，恰好匹配，不会出现跨过丢掉的袜子去和别人匹配的情况。所以只能丢奇数位置的袜子。

假设我们在从后向前模拟枚举时，你会发现我们是跳着走的，右边每次都恰好多出一对，前面恰好减少一对，剩余的都不变，好——>前缀和优化。这样就能降到O(n)了。然后计算最优答案即可?

#include <bits/stdc++.h>
using namespace std;
int a[300000];
long long ans;
int main(){
	int n,k;cin>>n>>k;
	for(int i=0;i<k;i++)
		cin>>a[i];
	if(k&1){
		vector<ll> suf(k);//定义前缀和suf，suf[0]表示前一个，suf[2]表示前两个(0,1)，suf[4]表示前四个(0,1,2,3)，suf[k-1]表示前k-1个(0~k-2)
		for(int i=1;i<k;i+=2){//k一定是奇数，所以从1开始遍历，一直遍历到k-2，那么suf就到suf[k-1]
			suf[i+1]=a[i]-a[i-1];
			if(i>1) suf[i+1]+=suf[i-1];
		}
		ans=suf[k-1];//k-1个袜子的前缀和(0~k-2号袜子)，这种情况对应最后一个袜子丢掉的答案
		int now=0;
		for(int i=k-2;i>=0;i-=2){//k-2是奇数
			now+=a[i+1]-a[i];//加上右边不断多出来的袜子对
			ans=min(ans,now+suf[i-1]);
		}
	}
	else {
		for(int i=1;i<k;i+=2){//k是偶数时候，k-1是奇数，刚好全部配对
			ans+=a[i]-a[i-1];
		}
	}
	cout<<ans;
}