【遥感数字图像处理（朱文泉）】第四章 变换域处理方法

4 1 变换域处理方法概述

?一、变换域处理的优势
?二、变换域处理方法

难点：各变换算法很抽象，尤其是傅里叶变换与小波变换
重点：各变换算法在图像处理中的物理含义及应用

一、空间域与变换域

? - 换一个角度来看数字图像
?空间域图像直观地为我们提供了丰富的空间和数字信息，但如果我们将空间域图像进行某种变换，将会较为容易地识别出一些在原始图像上无法直观看到的信息，从而有利于图像的后续处理。（空间域和变换域之间是一种互补的关系）

二、变换域处理方法

?1、主成分分析
?2、最小噪声分离
?3、缨帽变换
?4、傅里叶变换
?5、小波变换
?6、颜色空间变换

?其中，线性变换：主成分分析、最小噪声分离、缨帽变换；频率域变换：傅里叶变换、小波变换。

4 2 主成分变换

?一、主成分变换的概念
?二、主成分变换原理
?三、主成分变换过程
?四、遥感图像主成分变换及应用

一、主成分变换的概念

?主成分变换：又称主成分分析（Principal Components Analysis，PCA），将一组可能相关的变量转换到一组线性不相关的变量（称为主成分）的统计分析过程。

二、主成分变换原理

?在图(a)中，可以看出，主成分X1和X2是相关的一组主成分变量，将图中PC1、PC2旋转得到图(b)。观察图(b)，主成分PC1、PC2已经没有相关性了；原本的主成分X1、X2经过主成分变换，大部分信息都集中在主成分PC1上了，而主成分PC2上的信息减少（通过主成分变换，将信息集中到第一主成分上去）。

三、主成分变换过程

?主成分变换原则说明：任何一个主成分之间是没有关系的（z1、z2……）。

四、遥感图像主成分变换及应用

（上图展示各波段的空间结构）

（上图中可以看出各分量之间互不相关，如：PC1左上偏亮，PC2左上偏暗）

（上图展示图像增强方面的应用）

?主成分变换应用说明：
?（1）图像压缩：比如上面那个主成分变换的例子，原始的波段有七个，变换成七个主成分，把后面几个主成分去掉，只保留前面三个主成分，反变换之后，还是可以恢复到原始的空间图像；
?（2）图像去噪声：再如上面的例子，第七个主成分中有噪声，把第七个主成分去掉，再把前面的六个主成分反变换，就可以实现多波段图像噪声的去除（去噪声方法很多，这里只是其中一种方法）；
?（3）图像增强：如上图展示，有一幅原始影像是真彩色合成的（第一个图），现在前面三个主成分用假彩色合成，可以看出第二幅图与第一幅图相比，第二幅图体现的信息量是很多的，更容易区分地物细节（包括水体部分，含有的层次更丰富一些）；
?（4）图像融合；
?（5）特征提取（主成分变换最大的用处）：前面把七个波段进行主成分变换之后，它的大部分信息都集中在前面三个主成分上，所以我们可以利用前面三个主成分就可以把它当作特征了。

4 3 最小噪声分离变换

?一、最小噪声分离变换的概念
?二、最小噪声分离变换原理及过程
?三、遥感图像最小噪声分离变换及应用

一、最小噪声分离变换的概念

?最小噪声分离（Minimum Noise Fraction，MNF），一种正交变换，变换后得到的各分量互不相关，各分量按照信噪比从大到小排列; MNF变换后使噪声得到了分离，且波段间不相关，所以它比PCA变换更加优越。

二、最小噪声分离变换原理及过程

?MNF变换相当于进行两次PCA。
?具体计算方法：
??1、噪声估计；
??2、对噪声图像进行主成分变换，获得用于随机噪声分离和调整的变换矩阵；
??3、对原始遥感影像各波段的随机噪声进行分离和重新调整；
??4、对经噪声分离和重新调整的原始遥感影像进行主成分变换。

三、遥感图像最小噪声分离变换及应用

（可以与前面PCA图像结果进行异同观察 ：MFN各分量之间也是互不相关的，信息量也主要集中在前三个里面）

4 4 缨帽变换

?一、缨帽变换的概念
?二、缨帽变换模型
?三、遥感图像缨帽变换及应用

一、缨帽变换的概念

?一种基于图像物理特征的固定转换，变换后的坐标轴不是指向主成分方向，而是指向与地面景物有密切关系的方向，特别是与植物生长过程和土壤有关。

?区别：PCA和MNF之间的物理意义是不明确的，即在不同的影像获取的主成分，它们之间不具有可比性；但是对于缨帽变换来说，对于同一个地方、不同时间、同一个传感器获取的影像经过缨帽变换之后，各个分量之间是具有可比性的。

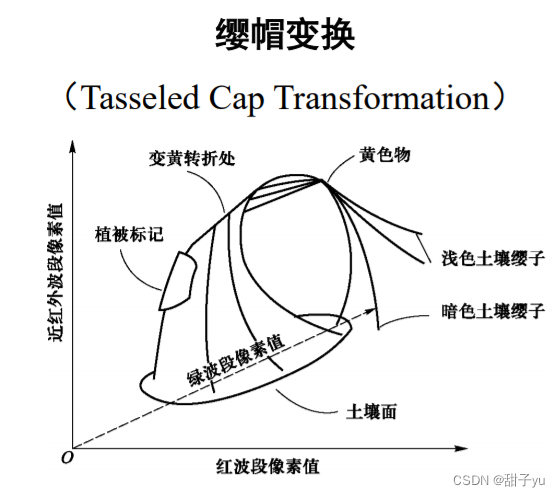
二、缨帽变换模型

三、遥感图像缨帽变换及应用

?常见分量：
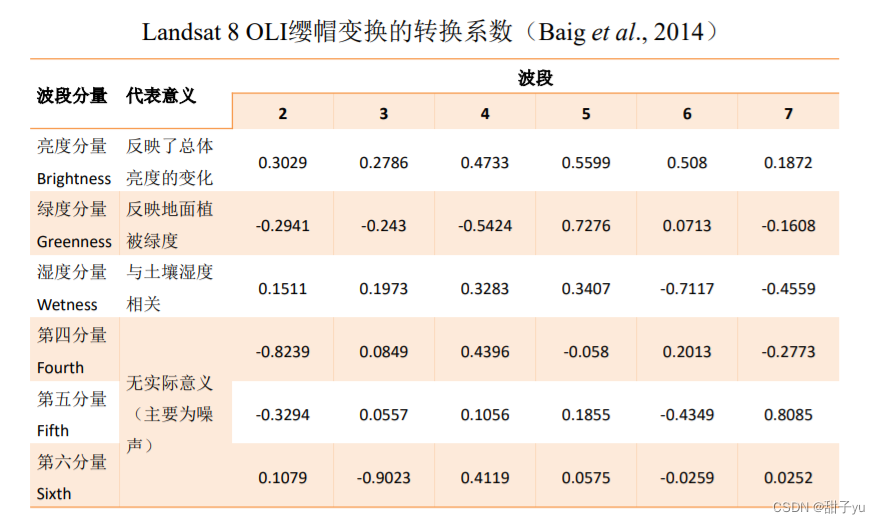
??亮度分量（Brightness）：波段分量的加权和，反映了总体的亮度变化；
??绿度分量（Greenness）：与亮度分量垂直，是近红外与可见光波段的比值，反映可见光波段特别是红光波段与近红外波段之间的对比，即地面植被的绿度；
??黄度分量（Yellow Stuff）：反映植被的枯萎程度；
??湿度分量（Wetness）：与土壤湿度有关，反映可见光与近红外波段及红外波段的差值；
??无意义分量（Non-such）：无实际意义，通常为噪声。

4 5 傅里叶变换

?一、傅里叶变换在信号处理中的作用
?二、数字图像中的频率
?三、数字图像傅里叶变换的含义
?四、傅里叶变换在数字图像处理中的应用

一、傅里叶变换在信号处理中的作用

?傅立叶变换是一种通过频率来分离不同信号的方法。
?如：一束太阳白光经三棱镜被分解为红、橙、黄、绿、蓝、靛、紫不同频率的单色光

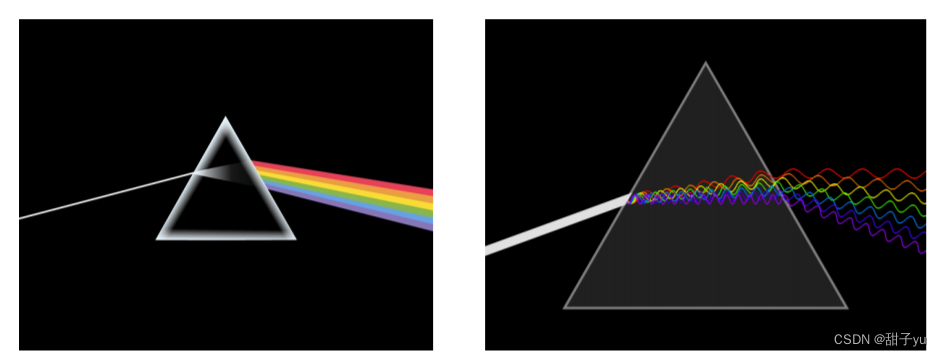
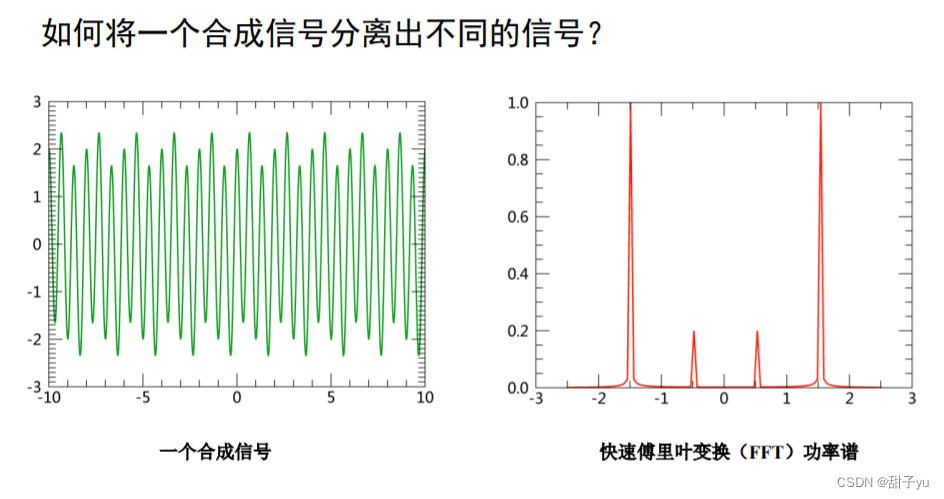
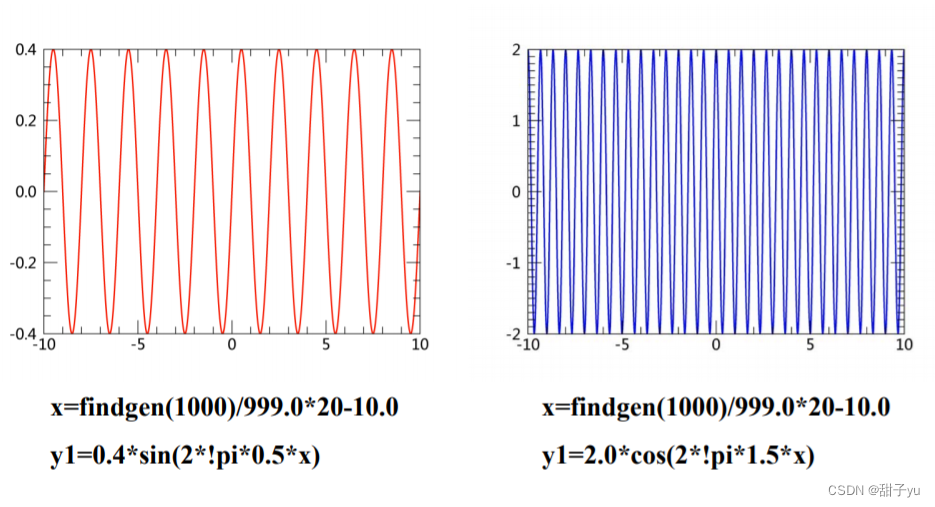
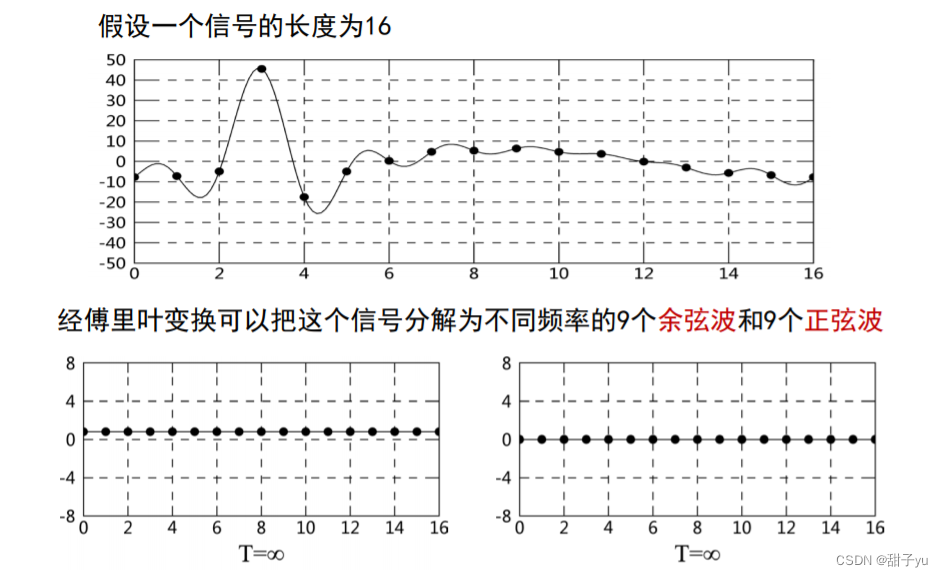
（这里是动态变换的两个正弦/余弦图象）

二、数字图像中的频率

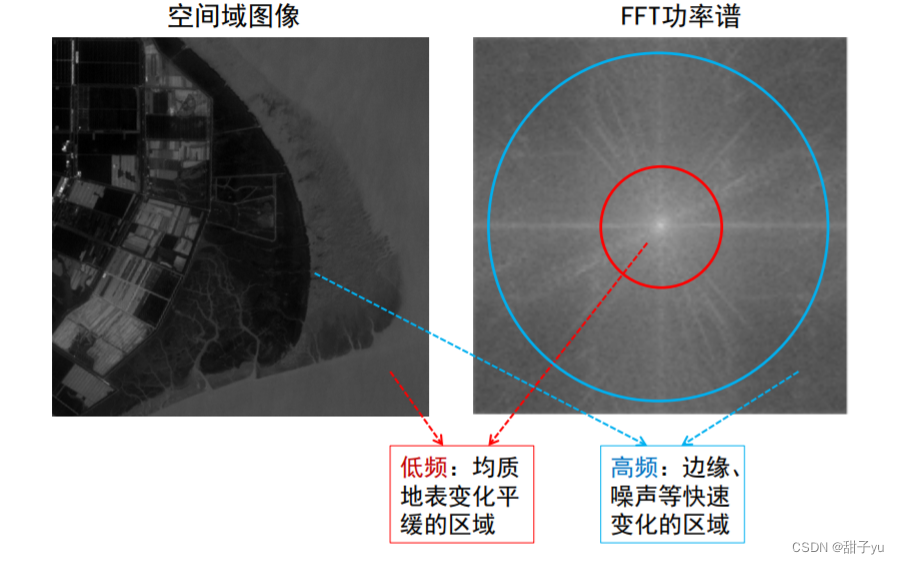
?注意：傅里叶变换的频谱图上任何一个像元点不是和空间域的像元点一一对应的，它的计算是由空间上所有的像元都参与运算后得到的一个结果。

三、数字图像傅里叶变换的含义

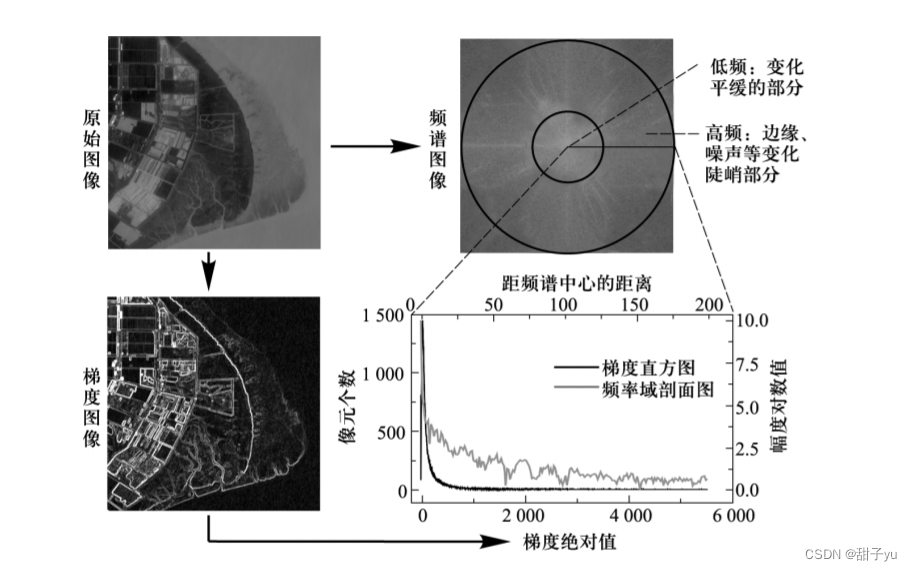
?原始图像所看到的空间结构是因为不同像元之间的灰度值是不一样的，把它的灰度分布通过傅里叶变换变成了一个频率分布，从中间越往两边，由低到高。实质上，我们可以这样来理解，这张频谱图就相当于原图上的梯度图里的直方图。也就是说，我们对原图求梯度，梯度就是（图像空间结构里）边缘这样的一个信息。因为梯度图像有的是正的，有的是负的，所以先对梯度图像求绝对值，再求直方图，就对应第四幅图里实线的部分。梯度直方图中，大部分梯度值是比较低的，少部分梯度较高，对应梯度图像中较平坦的地方、水域部分的梯度值较小，边缘部分梯度值比较高。再看频谱图，从中间部分到边缘，及对应第四幅图中虚线部分（频率域剖面图），实线部分与虚线部分是大致符合的。遥感图像经过傅里叶变换，它的高频部分就对应边缘，即梯度绝对值比较高的部分。

四、傅里叶变换在数字图像处理中的应用

（去噪声示例）

4 6 小波变换

?一、小波
?二、小波变换优势
?三、数字图像小波变换
?四、小波变换在数字图像处理中的应用

一、小波

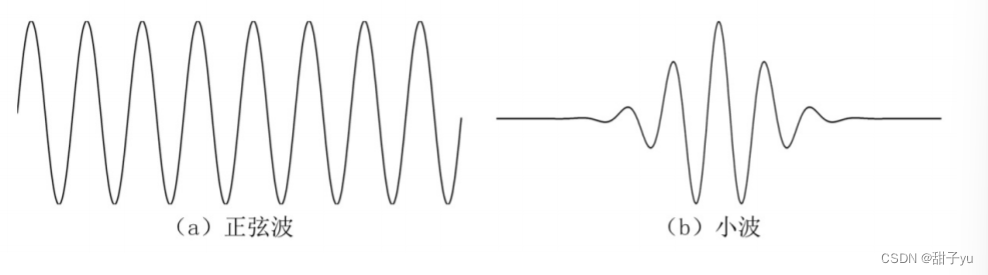
?小波变换与傅里叶变换类似，都是把一个信号分解成一组正交信号，但不同于傅里叶变换中使用的三角函数，小波变换是用由零开始由零结束、中间为一段震荡的波来表示信号，它是一种能量在时域非常集中的波。

二、小波变换优势

?突变信号的傅里叶变换:
??对于突变信号，即使只有一小段变换，傅立叶也不得不用大量的三角波去拟合，并且会出现Gibbs现象。

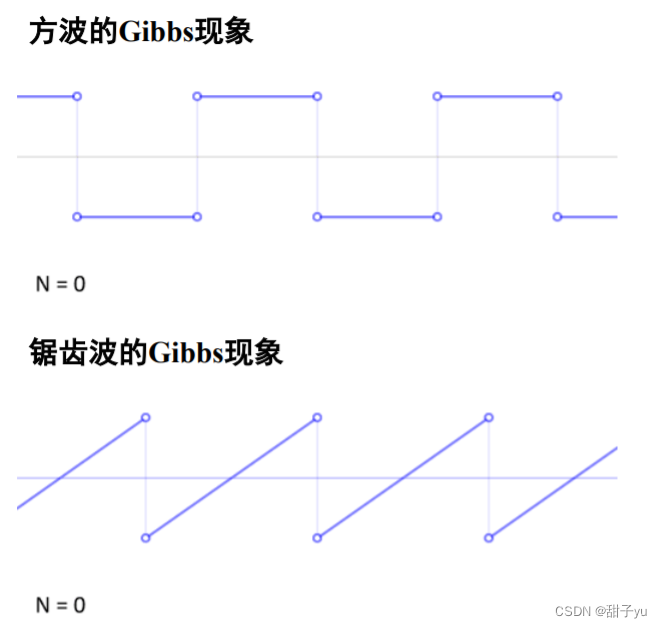
（这里是动态变换的图） ?突变信号的小波变换：
??如果我们用小波去拟合这种阶跃信号，只要小波基函数不和这个信号变化重叠，它所对应级数的小波系数则为0。

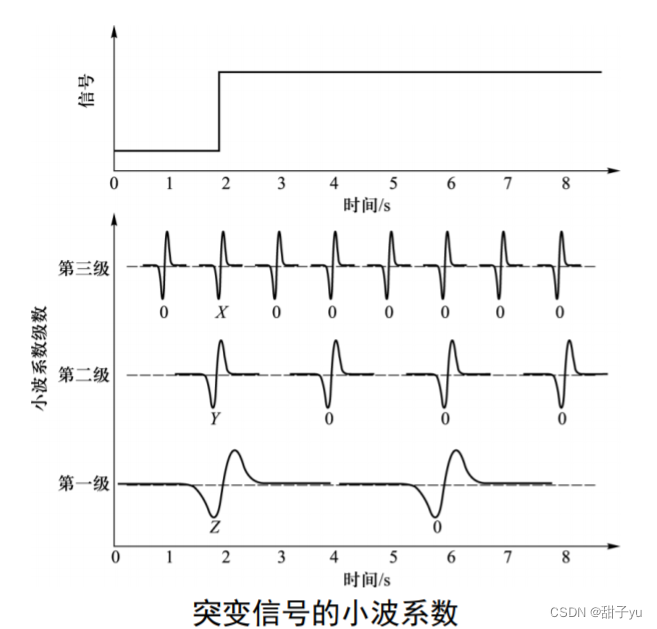
三、数字图像小波变换

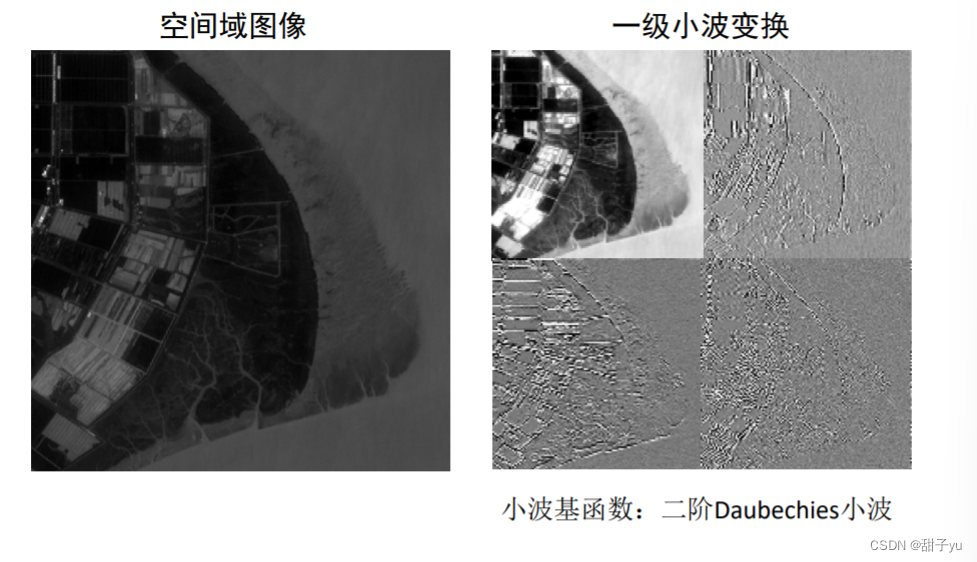
四、小波变换在数字图像处理中的应用

?小波变换相当于把图像的频率分离了，把不同的高频分成不同的层次。其应用与傅里叶变换相似。（小波变换图像压缩频率很高，失真也比较小）

4 7 颜色空间变换

?一、颜色空间的概念
?二、颜色空间分类
?三、常用颜色空间
?四、颜色空间之间的相互转换
?五、颜色空间变换在图像处理中的应用

一、颜色空间的概念

?颜色空间是用一种数学方法来形象化地表示颜色，颜色空间常用来指定和产生颜色。
?颜色空间中的颜色通常用代表3个参数的3维坐标来描述，其颜色要取决于所使用的坐标。大部分遥感数据都采用RGB颜色空间来描述，但对图像进行一些可视分析时，也会使用其他颜色空间（如HSI模型）。

二、颜色空间分类

?从颜色感知的角度可将颜色空间分为混合型颜色空间（如RGB颜色空间）、非线性亮度/色度型颜色空间（如YUV颜色空间）和强度/饱和度/色度型颜色空间（如HSI颜色空间）。而从技术应用的角度来看，颜色空间又可以分为计算机图形颜色空间（如RGB颜色空间）、CIE颜色空间（如XYZ颜色空间）、和电视系统颜色空间（如YUV颜色空间）。

三、常用颜色空间

?RGB颜色空间：通过红（Red）、绿（Green、）蓝（Blue）三原色来描述颜色的颜色空间。
?物理三基色：红（700nm）、绿（546.1nm）、蓝（435.8nm）。

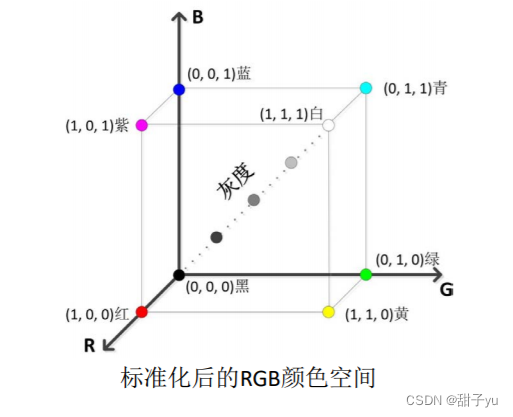
?CMY(K)颜色空间：青-品红-黄（Cyan-Magenta-Yellow，CMY）颜色空间主要应用于彩色图象印刷行业，这三种颜色是光的二次色，也就是颜料的原色。（打印彩色图像时，我们一般把RGB转换成CMY，原因是打印时可能有的RGB颜色没有，打印不出）
?在CMY模型中，颜色是从白光中减去一定成分得到的。例如：当青色（0，1，1）颜料覆盖的表面用白色光（是等量的红、绿、蓝光的组合）照射时，该表面反射的不是红光，而是从反射的白光中减去被颜料吸收的红色。

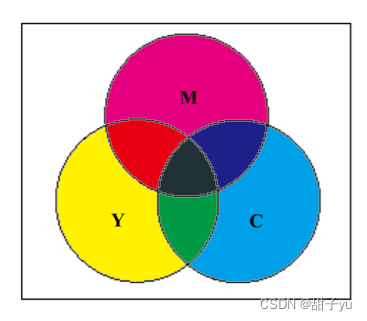
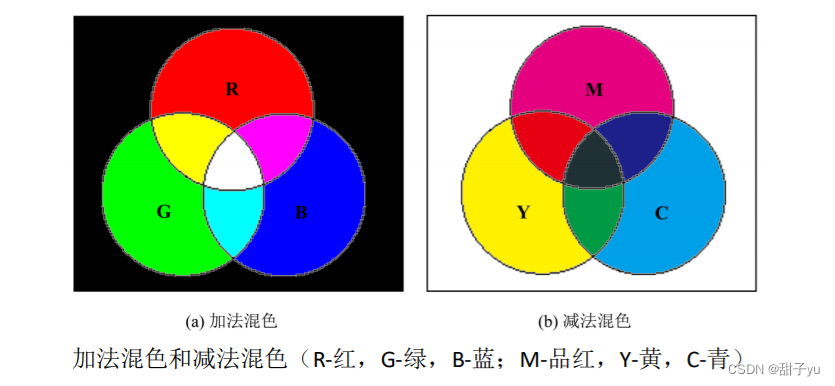
?加法混色中的红色（0, 0, 1）和绿色（0, 1, 0）的混合，相当于将两个颜色向量相加(0, 0, 1)+(0, 1, 0)=(0, 1, 1)，即黄色。
?减法/乘法混色中的青色(0, 1, 1)和黄色(1, 1, 0)的混合，相当于将两个颜色向量矢量相乘(0, 1, 1)×(1, 1, 0)=(0, 1, 0)，即绿色。

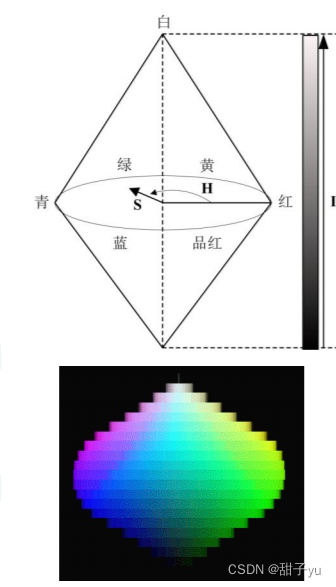
?HSI颜色空间（Hue-Saturation-Intensity），用色调(H)、色饱和度(S)和亮度(I)来描述。
??H：是颜色的主波长，值从红色中点处的0开始，沿球体圆周逆时针方向增加，最后到255(红→橙→黄→绿→青→蓝→紫→红)；
??S：由距中轴线的距离表示，描述了色彩的纯度，其值在中心的0（不纯的颜色）到圆周处的1之间；
??I：由垂直坐标表示，在黑色（0）到白色（255）之间变化，确定像元整体亮度，与色彩无关。

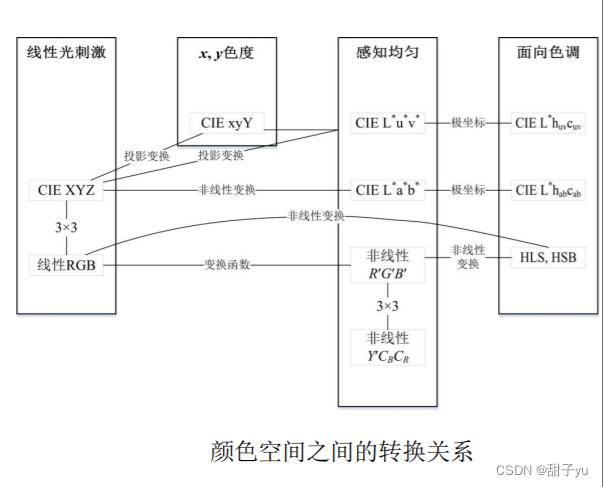
四、颜色空间之间的相互转换

?颜色空间之间的转换关系可以分类两类：一类是颜色空间之间可以直接转换，如RGB和HSL；另一类是颜色空间之间不能直接转换，它们之间的变换需要通过借助其他颜色空间的过渡来实现，如，RGB和CIE L * a * b *。

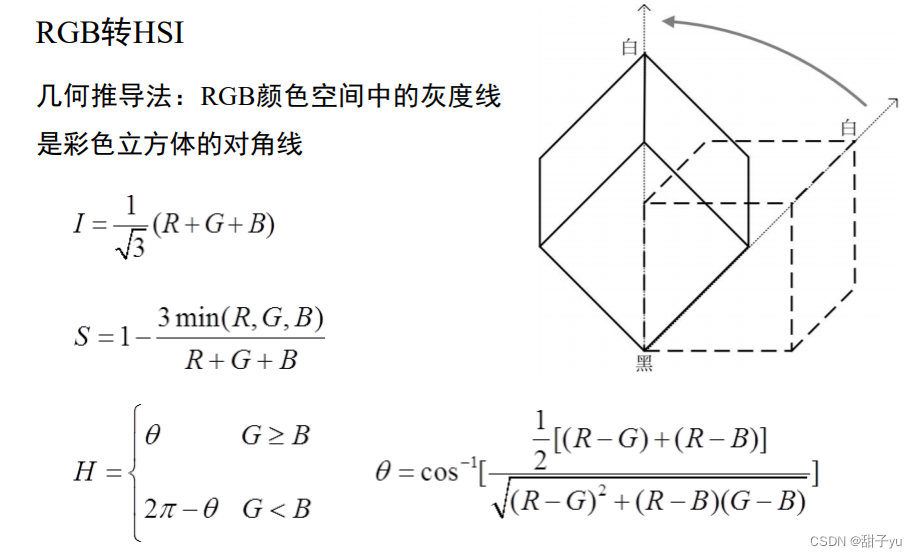
五、颜色空间变换在图像处理中的应用